elementi di statistica  descrittiva

Per  DISTRIBUZIONI  UNIVARIATe

 

 

1.8.   Indici di forma: SIMMETRIA E CURTOSI

 

 

Gli indici di forma di una distribuzione riguardano 2 caratteristiche: la simmetria e la curtosi.

A differenza di quanto avvenuto nello studio della variabilità, nell'analisi della forma di una distribuzione statistica le misure elaborate sono rimaste rudimentali e le stesse definizioni sono sovente equivoche. Inoltre l’uso degli indici di forma non rientra nei test d’inferenza, ma è limitato alla semplice descrizione della forma della distribuzione.

Nelle distribuzioni unimodali si ha simmetria quando media, moda e mediana coincidono; se la distribuzione è bimodale, possono essere coincidenti solamente la media aritmetica e la mediana.

Di norma, le distribuzioni dei dati sono unimodali; pertanto, l’analisi della simmetria  è accentrata su di esse.

In una distribuzione,

-          l'asimmetria è detta destra (più correttamente, a destra) quando i valori che si allontanano maggiormente dalla media sono quelli più elevati, collocate a destra dei valori centrali (figura 19); nell’asimmetria destra, la successione delle 3 misure di tendenza centrale da sinistra a destra è: moda, mediana, media;

-          l'asimmetria è detta sinistra (o a sinistra) quando i valori estremi, quelli più distanti dalla media, sono quelli minori (figura 20). Nell’asimmetria sinistra, la successione delle 3 misure di tendenza centrale da sinistra a destra è invertita rispetto all'ordine precedente: media, mediana, moda.

 

Quando media, mediana e moda non coincidono, la  distribuzione è asimmetrica; ma quando queste tre misure coincidono non sempre la distribuzione è simmetrica. Per avere una distribuzione simmetrica, la perfetta coincidenza delle tre misure di tendenza centrale è condizione solo necessaria, non sufficiente.

Infatti, supponendo di analizzare una distribuzione come

-          16  20  20  20  30  30

 troviamo che

-          la media (140/7 = 20),

-          la mediana (su 7 valori è il 4° = 20) e

-          la moda (il valore più frequente è 20)

 sono coincidenti (20); ma, come si evidenzia dalla semplice lettura dei dati, la sua forma non è simmetrica poiché i dati non declinano in modo regolare ed identico dalla tendenza centrale verso i due estremi.

Un altro metodo proposto per valutare la simmetria utilizza la distanza delle classi di frequenza dalla mediana: una distribuzione è simmetrica, se i valori che sono equidistanti dalla mediana hanno la stessa frequenza. Ma è possibile dimostrare che si tratta di una condizione che si realizza sia in distribuzioni unimodali che plurimodali; è quindi una definizione che non caratterizza la distribuzione simmetrica in modo biunivoco, non è vera esclusivamente in una distribuzione normale.

 

 

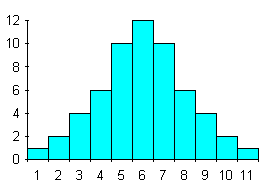
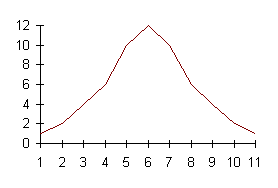
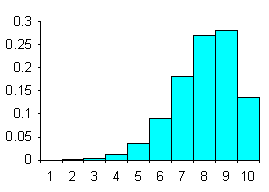
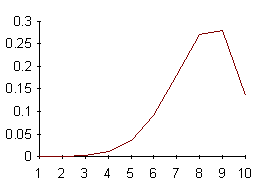
I grafici di seguito riportati evidenziano la forma di una distribuzione simmetrica (Fig. 18),

 

 

.

Figura 18.  Distribuzioni simmetriche, con istogrammi e con poligoni

 

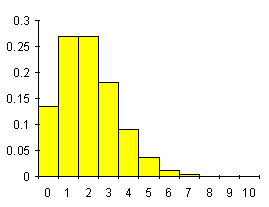
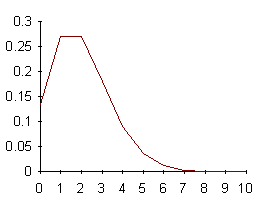
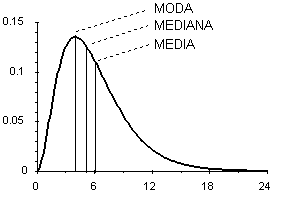
quella di una distribuzione destra o positiva (Fig. 19)

 

             

Figura 19.  Distribuzioni con asimmetria a destra, con istogrammi e con poligoni

 

 

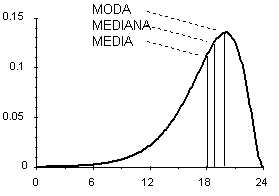
e quella di una distribuzione sinistra o negativa (Fig. 20).

 

 

             

Figura 20.  Distribuzioni con asimmetria a sinistra, con istogrammi e con poligoni.

 

 

Analizzando la distribuzione in classi dei dati di un campione, è possibile osservare un'asimmetria causata da un numero ridotto di osservazioni oppure da modalità non adeguate nel raggruppamento in classi, di solito eccessivo; in questi casi, si parla di asimmetria falsa, da distinguere dalla asimmetria vera, che può esistere solo nella distribuzione reale di una popolazione.

Una proprietà essenziale degli indici di asimmetria di una distribuzione è che essi dovrebbero essere uguali a zero quando, e solamente quando, la distribuzione è simmetrica.

E' una proprietà che si realizza per gli indici abituali di variabilità o dispersione, come la devianza, la varianza e le misure derivate; esse sono nulle quando, e solamente quando, tutti i valori sono uguali, e quindi non esiste variabilità; quando non sono nulle, esiste una variabilità, che cresce all’aumentare del valore dell’indice.

Gli indici di simmetria non godono della stessa proprietà: quando la distribuzione è simmetrica sono nulli; ma possono essere nulli anche per distribuzioni non simmetriche.

Per valutare l'asimmetria di una distribuzione, si possono usare

-          misure dell'asimmetria assoluta

  misure di asimmetria relativa.

Gli indici di asimmetria assoluta si esprimono con le distanze tra la media e la moda o la mediana.

Una misura assoluta, usata frequentemente, è la differenza (d) tra la media e la moda:

d = media - moda

La differenza è:

   d = 0,  se la curva è simmetrica;

   d > 0,  se la curva ha asimmetria positiva (o destra : media > mediana > moda);

   d < 0,  se la curva ha asimmetria negativa (o sinistra : media < mediana < moda).

 

Figura 21.  Asimmetria destra o positiva (d>0)      Figura 22.  Asimmetria sinistra o negativa  (d<0)

 

 

E' possibile valutare in modo molto semplice ed empirico il grado d’asimmetria di una distribuzione; essa è ritenuta moderata se

Moda = Media - 3(Media - Mediana)

ed è ritenuta forte se è sensibilmente maggiore di tale valore.

 

Per ottenere una misura del grado di asimmetria, che possa essere confrontato con quello di qualsiasi altra distribuzione in quanto indipendente dalle dimensioni delle misure, occorre utilizzare indici relativi, quali

   skewness di Pearson;

   ₁ di Fisher;

   ₁ di Pearson.

 

L’indice skewness di Pearson (sk) è un rapporto: la differenza (d) tra la media e la moda è divisa per la deviazione standard () o scarto quadratico medio. Nel caso di una distribuzione campionaria, dove la deviazione standard è indicata con s, è

Come per il valore d precedente, sk può essere nullo, positivo o negativo secondo la forma della distribuzione.

Essendo un rapporto tra misure statistiche della stessa distribuzione, è divenuto una misura adimensionale, indipendente dal valore assoluto degli scarti dalla media; quindi può essere utilizzato per il confronto tra due o più distribuzioni.

 

Un altro indice di simmetria, proposto da A. L. Bowley nel 1920 ( vedi il testo Elements of Statistics, Charles Scribner’s Sons, New York), chiamato appunto Bowley coefficient e riproposto in alcuni programmi informatici, utilizza i quartili (

 

Skewness =

dove

-          Q₂ = valore della mediana o del secondo Quartile

-          Q₁ = valore del primo quartile,

-          Q₃ = valore del terzo quartile.

Il valore ottenuto è uguale a zero se la distribuzione è perfettamente simmetrica, mentre è negativo o positivo in rapporto al tipo di asimmetria, in modo analogo alle formule precedenti.

 

Anche la curtosi, la concavità della distribuzione di dati (più ampiamente spiegata nel prosieguo del paragrafo), può essere misurata con i quantili o meglio gli ottili, come proposto da J. J. A. Moors nel 1988 (nell’articolo A quantile alternative for kurtosis, su Statistician Vol. 37, pp. 25-32).

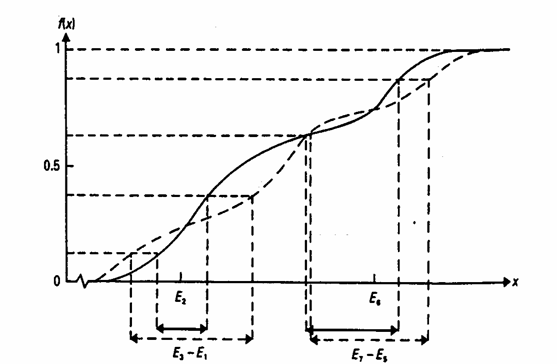
Il concetto di base è che la curtosi può essere interpretata come una misura di dispersione intorno ai due valori limite dell’intervallo , con una misura alternativa a quella parametrica, che è fondata sul momento di quarto ordine. Quando si confrontano testi differenti, l’interpretazione della curtosi è controversa, poiché molti la descrivono come un eccesso o un difetto di valori solo nella classe centrale, mentre la differenza dalla normale riguarda più punti.

Utilizzando i quantili o meglio gli ottili (indicati ovviamente con E nel testo in inglese), si ottiene

 

T =

 dove

-          E₁ è la metà di un quartile, cioè il  valore che occupa il 12,5 percentile,

-          E₂, E₃, … sono multipli di esso, fino a E₇ corrispondente al 87,5 percentile.

 

 

 

Figura 23. Grafico degli ottili

 

Dal grafico risulta con evidenza come i due termini del numeratore,  (E₃ – E₁) e (E₇ – E₅), valutano la concentrazione di dati intorno a E₆ e E₂, corrispondenti ai punti . L’indice T è analogo alle misure di dispersione e simmetria più familiari fondate sui quantili e offre gli vantaggi simili; inoltre esclude i valori estremi e quindi è più robusto dell’indice parametrico fondato sui momenti..

Il denominatore (E₆ e E₂) è una costante di normalizzazione, che garantisce l’invarianza dell’indice T, nel caso di trasformazioni lineari (Vedere capitolo sulle trasformazioni).

Per distribuzioni che sono simmetriche intorno a 0,  la formula precedente

 può essere semplificata in

T =

 

 

Gli indici relativi della forma di una distribuzione attualmente più diffusi sono derivati dai momenti.

I momenti (m) di ordine k rispetto ad un punto c sono calcolati con

per una serie di dati 

e con

per una distribuzione di frequenza suddivisa in classi.

Abitualmente, con c si indica l'origine (c = 0) oppure la media (c = media). Nel primo caso, si parla di momento rispetto all'origine; nel secondo, di momento centrale.

 

Il momento di ordine 1 (k = 1) rispetto all'origine dei valori (c = 0) è la media;

il momento centrale (c = m) di ordine 1 (k = 1) é uguale a 0 (è la somma degli scarti dalla media).

 

Il momento centrale (c = m) di ordine 2 (k = 2) è la varianza.

Nello stesso modo del momento centrale di secondo ordine (m₂), si possono calcolare i momenti centrali di ordine terzo (m₃), quarto (m₄), quinto (m₅),...ennesimo (m_n).

 

I momenti centrali di ordine dispari (m₃, m₅,...) sono utilizzati per indici di simmetria.

Essi sono nulli per distribuzioni simmetriche e differiscono da zero quando le distribuzioni non sono simmetriche; quanto maggiore è l'asimmetria, tanto più il valore del momento centrale di ordine dispari è grande. Inoltre, in distribuzioni con asimmetria destra ha un valore positivo ed in quelle con asimmetria sinistra ha un valore negativo.

Per queste sue caratteristiche, il momento centrale di terzo ordine (m₃) è adeguato per valutare la simmetria o asimmetria di una distribuzione; ma esiste il limite che il suo valore dipende dalla scala utilizzata.

Per ottenere una misura relativa, adimensionale, che permetta i confronti tra più distribuzioni, bisogna dividere m₃ per il cubo dello scarto quadratico medio.

E' l'indice ₁ (coefficient of skewness) di Fisher

detto anche il momento standardizzato di terzo ordine e che mantiene le proprietà precedentemente descritte.

I momenti centrali di ordine dispari sono nulli, quando la distribuzione è simmetrica; sono positivi o negativi rispettivamente quando vi è asimmetria destra o sinistra.

Nel caso di una distribuzione di dati sperimentali, l’indice di asimmetria (coefficient of skewness) è indicato con g₁.

Per valutare il grado di asimmetria, è convenzione che si abbia una distribuzione ad asimmetria

   forte, quando  |g₁| > 1;

   moderata, quando   ½ < |g₁| < 1;

   trascurabile, quando  0 < |g₁| < 1/2.

 

L'indice di asimmetria ß₁ di Pearson , storicamente antecedente al ₁ di Fisher, è stato definito come

Quando calcolato su una distribuzione sperimentale è indicato con b₁.

Fisher ha solo semplificato l'indice di Pearson,

mediante la relazione semplice

 

ma nella pratica della statistica si è affermato il suo metodo.

 

E’ utile ricordare quanto già ripetuto alcune volte:

-  nel caso di distribuzioni simmetriche i 3 indici  sk,  ₁,  ß₁  danno un risultato uguale a 0;

-  ma non sempre vale l'inverso, non sempre un indice di asimmetria uguale a 0 caratterizza la simmetria perfetta di una distribuzione di dati.

 

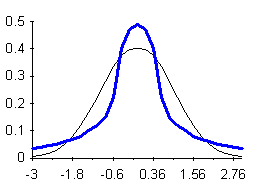
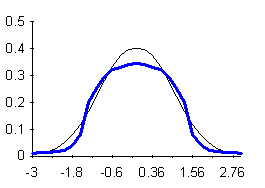
Quando si descrive la forma delle curve unimodali simmetriche, con il termine curtosi (dal greco kurtos, che significa curvo o convesso) si intende il grado di appiattimento, rispetto alla curva normale o gaussiana (le cui caratteristiche saranno discusse in modo più approfondito nel capitolo dedicato alle distribuzioni teoriche).

Nella valutazione della curtosi, una distribuzione unimodale simmetrica è detta:

-          mesocurtica , quando ha forma uguale alla distribuzione normale;

-          leptocurtica (figura 23), quando ha un eccesso di frequenza delle classi centrali, una frequenza minore delle classi intermedie ed una presenza maggiore delle classi estreme; è quindi una distribuzione più alta al centro e agli estremi e più bassa ai fianchi; la caratteristica più evidente è l'eccesso di frequenza dei valori centrali;

-          platicurtica (figura 24), quando rispetto alla normale presenta una frequenza minore delle classi centrali e di quelle estreme, con una frequenza maggiore di quelle intermedie; è quindi una distribuzione più bassa al centro e agli estremi mentre è più alta ai fianchi; la caratteristica più evidente è il numero più ridotto di valori centrali.

 

 

              

      Figura 24.  Distribuzione leptocurtica                           Figura 25.  Distribuzione platicurtica

                         rispetto alla mesocurtica                                               rispetto alla mesocurtica

 

 

L'indice di curtosi è il risultato di un confronto, è un rapporto; quindi, è una misura adimensionale.

I due indici di curtosi più utilizzati sono analoghi a quelli di asimmetria:

-  l'indice ₂ di Fisher (g₂ in una distruzione di dati osservati)

-  l'indice ₂ di Pearson (b₂.in una distribuzione di dati osservati)

 

L'indice ₂ di Fisher è fondato sul rapporto

 

Se la distribuzione è perfettamente normale, il risultato del calcolo è uguale a 3; è maggiore di 3 se la distribuzione è leptocurtica, mentre è minore di 3 se la distribuzione è platicurtica.

 

Per spostare la variazione attorno allo 0, l'indice di curtosi di Fisher è scritto come

 

Ovviamente, il risultato diviene

   0,  se la distribuzione è normale o mesocurtica,

   positivo,  se la distribuzione è leptocurtica o ipernormale,

  negativo, se la distribuzione è platicurtica o iponormale

 

Mentre l’indice g₁ può variare tra  ± ¥, l’indice g₂ può variare tra  - 2  e  + ¥; non è quindi possibile associare ad esso una gradazione in valore assoluto che valuti l’intensità della curtosi.

Come già precedentemente discusso, le condizioni che  g₁ e g₂ = 0 sono necessarie ma non sufficienti, affinché la curva sia simmetrica e mesocurtica.

 

L'indice ß₂ di Pearson è il rapporto fra il momento centrale di quarto ordine e la deviazione standard, elevato alla quarta potenza:

Il suo legame con ₂ di Fisher è semplice, di tipo lineare:

 

Come l'indice g₂ varia attorno a 0,  ß₂ varia attorno a 3.

 

Tutti gli indici presentati, dalle misure di tendenza centrale a quelle di dispersione e di forma, sono validi sia per variabili discrete che continue, con l'ovvia approssimazione data dal raggruppamento in classi.

 

Quando simmetria e curtosi sono stimate non sulla popolazione (g₁ e g₂)  ma su un campione (quindi indicate con i corrispondenti simboli latini g₁ e g₂),

g₁ in valore assoluto tende a  sottostimare g₁ ( |g₁| < |g₁| ); infatti è possibile dimostrare che, in un campione di dimensioni n, non supera il valore della radice di n

 

Problemi simili esistono per la stima di g₂ in piccoli campioni con forte curtosi.

I limiti di g₂ sono

 

Con dati campionari, simmetria e curtosi sono ovviamente calcolati da distribuzioni di frequenza raggruppate in classi.

Definendo

-  k   =   numero di classi di frequenza

-  f_i   =   frequenza della classe i,

-    =  valore centrale della classe i

-    =  media generale del campione

-  s   =   deviazione standard del campione

e da essi avendo ricavato

e

si calcola g₁ con

e g₂ con

 

I valori di g₁ e g₂ sono adimensionali: in altri termini, il risultato è identico, qualunque sia la misura utilizzata o la trasformazione applicata alla variabile X.

Alla fine del capitolo 10 sono riportati i test proposti da Snedecor e Cochran sul loro testo Statistical Methods, per valutare la significatività di g₁ e g₂ in campioni di grandi dimensioni (oltre 100 dati).