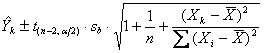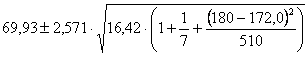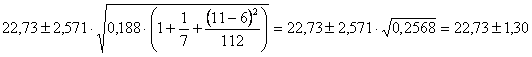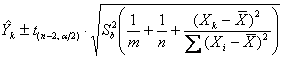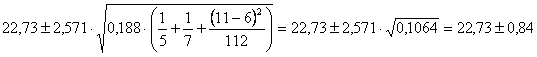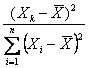|
LA REGRESSIONE LINEARE SEMPLICE
16.12. INTERVALLO DI CONFIDENZA O DI PREVISIONE DI
Costruita una retta
con - la stima per un valore aggiuntivo (additional measurement) al campione. Un’esigenza frequente nella ricerca è il successivo calcolo - dell'intervallo
di previsione (detto anche intervallo di confidenza, seppure in modo meno
corretto) di questo valore
Anche in questo
caso, il valore medio collocato sulla retta
oppure con la formula equivalente
con modalità del tutto identiche a quelle illustrate nel paragrafo precedente. Il suo intervallo di previsione (prediction interval) invece cambia e può essere calcolato mediante la formula
dove - la simbologia è quella del paragrafo precedente e - la parte sotto
radice è l’errore standard del valore
ESEMPIO 1 (CALCOLO DELL’INTERVALLO PER UN PUNTO AGGIUNTIVO, CON DATI BIOLOGICI). Con i dati dell’esempio sulla regressione tra altezza e peso
sui quali è stato
calcolato il punto medio per il valore aggiuntivo
- stimare alla probabilità a = 0.05 il suo intervallo di confidenza.
Risposta. Dalla formula prima presentata dove, sempre ricavati dai paragrafi precedenti, t(5,0.025)
= 2,571 si ottiene che per
sono dati da
Pertanto, - il limite inferiore è - il limite superiore è
Nella tabella successiva sono riportati
- i valori medi di
- gli intervalli di confidenza (L1, L2) alla probabilità a = 0.05 e a = 0.01, per gli stessi
valori Anche in questo
caso, è possibile osservare come gli intervalli per i valori collocati più
vicino alla media Ad esempio, per a = 0.05 con - - (la leggera differenza tra il valore dell’intervallo calcolato nell’esempio 1 e quello riportato nella tabella è imputabile all’uso di un numero diverso di decimali nel calcolo).
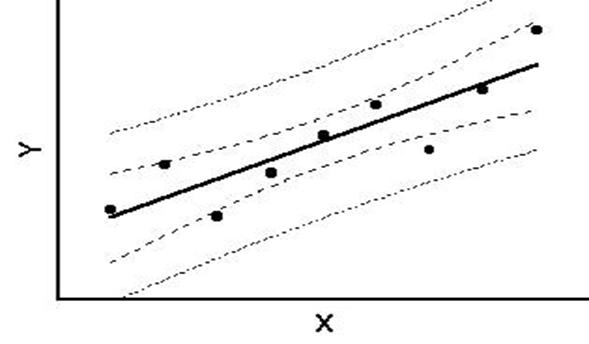
La rappresentazione grafica di questo intervallo evidenzia la distanza maggiore di questi dati dall’intervallo calcolato per i dati del campione.
ESEMPIO 2 (CALCOLO DELL’INTERVALLO PER UN PUNTO PREVISTO, CON DATI CHIMICI). Con i dati dell’esempio su concentrazione e intensità della fluorescenza,
dai quali (nei paragrafi precedenti) è stata calcolata la retta
- stimare alla
probabilità a = 0.05 l’intervallo di confidenza del valore medio
Risposta. Dapprima dalla formula della retta si ricava che per
il valore di Successivamente dalla formula
dove, sempre ricavati dai paragrafi precedenti, t(5,0.025)
= 2,571 si ottiene che per
sono dati da
Pertanto, - il limite inferiore è - il limite superiore è
In altre
condizioni, viene chiesto l’intervallo di previsione (prediction
interval) per il valore La formula da impiegare è
dove -
ESEMPIO 3 (CALCOLO
DELL’INTERVALLO DI PREVISIONE DI UN PUNTO
dai quali (nei paragrafi precedenti) è stata calcolata la retta
- stimare alla
probabilità a = 0.05 l’intervallo di confidenza del valore medio
Risposta. Dapprima dalla formula della retta si ricava che per
il valore di Successivamente dalla formula
dove, t(5,0.025)
= 2,571 si ottiene che per
sono dati da
e pertanto - il limite inferiore è - il limite superiore è
E’ importante
osservare che l’intervallo calcolato per la media di più dati è minore di
quello che si ricava per un singolo valore Un secondo aspetto
importante è che, anche in questo caso, nel calcolo dell’errore standard del
valore
detto valore di leva (leverage) dell’osservazione k sul valore della retta. Ne deriva che i
valori di
Un terzo
particolare importante della formula per la media di
è che, quando si ottiene la formula
che è quella proposta per la stima dell’intervallo di un punto previsto con i dati del campione.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||