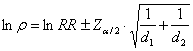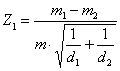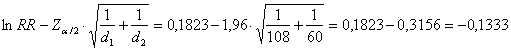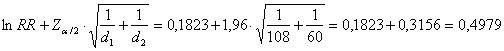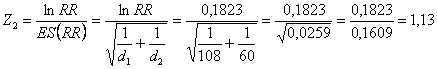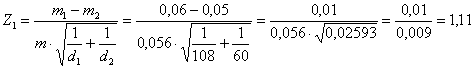PROPORZIONI E PERCENTUALI, RISCHI, ODDS E TASSI
5.17. IL RAPPORTO TRA DUE TASSI (RR): INTERVALLO DI CONFIDENZA E SIGNIFICATIVITA’; FORMULA TEST-BASED DI MIETTINEN
In demografia e in epidemiologia, proporzione e tasso (rate) hanno due significati chiaramente distinti, anche se spesso - vengono utilizzati per analizzare gli stessi fenomeni e - hanno valori simili quando le frequenza sono basse. Per meglio comprenderne le differenze, è didatticamente vantaggioso presentare gli eventi demografici e epidemiologici nel diagramma di Lexis. (Wilhem Lexis 1837-1914 si laureò all’Università di Bonn nel 1859 in scienze e matematica e si trasferì a Parigi nel 1861 dove condusse studi sulle discipline sociali, pubblicando soprattutto nel quinquennio 1976-1880).
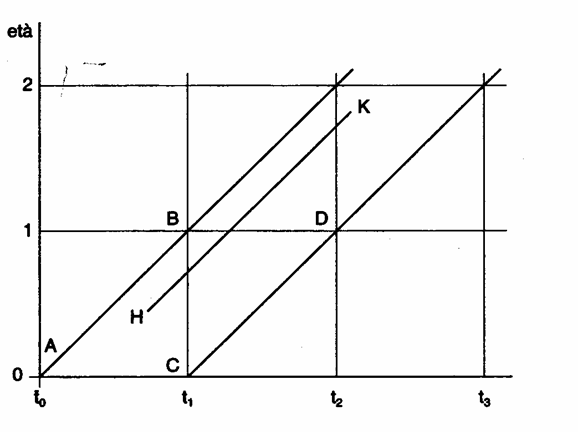
E’ un diagramma cartesiano, come quello riportato nella pagina precedente. Per un individuo, permette di rappresentare graficamente un evento nel tempo, considerando contemporaneamente due parametri fondamentali che lo misurano, - il tempo del calendario o le date, sull’asse delle ascisse; - la durata dell’evento oppure l’età dell’individuo, sull’asse delle ordinate.
Ad esempio, nella figura precedente si può osservare la rappresentazione grafica della storia clinica di un bambino che è entrato in osservazione nel momento H e ne è uscito nel momento K (per guarigione, morte oppure trasferimento): - la perpendicolare sull’asse delle ascisse dei due punti individua esattamente le due date, - la perpendicolare sull’asse delle ascisse individua la sua età nei due momenti.
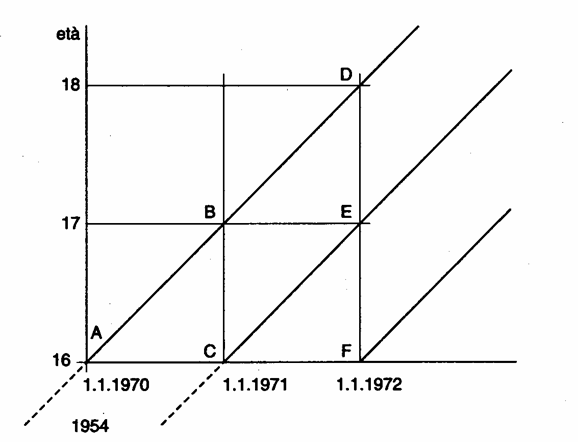
Ad esempio, si assuma che durante l’anno 1970, un gruppo di 180 giovani donne nel giorno del compimento del 16° anniversario (quindi appartenenti alla generazione nata nel 1954) si siano presentate a una visita di controllo per anemia, che siano state seguite tutte esattamente per un anno, fino al giorno del compimento del 17° anno. Se in quel periodo di osservazione 12 di esse hanno manifestato problemi gravi di anemia, nel grafico - le 180 giovani sono riportate sul segmento AC, - le 12 trovate positive sono riportate nel quadrilatero ABEC. Il rapporto ABEC/AC = 12/180 è la proporzione di ragazze con problemi gravi di anemia. Se riferita a una singola ragazza nelle stesse condizioni, è la probabilità che essa si ammali. Se le 12 fossero giovani decedute, in questo modo si sarebbe misurata la loro probabilità di decesso.
Ma condurre un'analisi su un gruppo non sempre è così semplice. Come prima, si supponga che durante l’anno 1970 un gruppo di 180 giovani donne nel giorno del compimento del 16° compleanno si siano presentate a una visita di controllo di anemia per essere seguite fino al compimento del 17° anno. Ma che non tutte siano state seguite esattamente per un anno, perché 30 di esse si sono trasferite in altra provincia e 10 nuove sono entrate. Se in quel periodo di osservazione 12 di esse hanno avuto problemi gravi di anemia, nel grafico - il numero medio di ragazze seguite è identificato dal segmento CB. - le 12 trovate positive come prima sono riportate nel quadrilatero ABEC. Il rapporto ABEC/CB è il tasso di ragazze con problemi gravi di anemia.
Come calcolare il numero medio di ragazze seguite? Esistono due modi ed entrambi richiedono una più esatta comprensione della trasformazione numerica del gruppo in osservazione: 1 - delle 180 ragazze iniziali, 30 sono emigrate dalla provincia; quindi le altre 150 sono state seguite per tutto l’anno; 2 – le altre 10 sono immigrate durante l’anno, per cui alla fine erano in 160.
Il primo metodo di calcolo è la media tra il numero iniziale e quello finale: (180 + 160) / 2 = 170 Nel grafico, questo 170 identifica il numero di persone che avremmo approssimativamente trovato facendo un loro censimento nel momento BC, cioè alla fine dell’anno 1970. Il secondo metodo implica il concetto di anni-vissuti. 1) Poiché 150 ragazze sono stata eseguite per tutto l’anno, si può dedurre che insieme esse hanno vissuto 150 anni (150 ragazze x 1 anno) di osservazione; 2) ognuna delle 30 ragazze che si sono allontanate durante l’anno approssimativamente sono state in osservazione per metà anno; ne deriva che complessivamente gli anni vissuti in osservazione da questa ragazze sono stati 15 (30 ragazze x 0,5 anni); 3) le 10 ragazze entrate in osservazione durante l’anno approssimativamente sono state in osservazione per metà anno; il loro contributo agli anni vissuti in osservazione è 5 (10 ragazze x 0,5 anni); 4) in conclusione, la somma di anni vissuti in osservazione è 170 (150 + 15 + 5).
Questo secondo metodo è di grande utilità in quanto permette facilmente, sulla base dei tempi della malattia, di calcolare giorni, settimane o anni di osservazione. Quindi, conoscendo il numero di eventi di quel periodo, di calcolare il tasso giornaliero, settimanale oppure della malattia. Ma è utile soprattutto quando si segue un gruppo non molto grande di individui, (ad esempio 200 persone), per un periodo lungo (ad esempio 20 anni) di follow-up. Il numero di anni persona (200 x 20) diventa 4000 e i valori dei tassi che si calcolano sono del tutto paragonabili al seguire 4000 persone per un anno. E’ uno sforzo di analisi e controllo che pochi gruppi di medici sarebbero in grado di fare. Inoltre, se alcuni pazienti si allontanano e altri entrano in osservazione, in questo modo il calcolo del valore medio è fatto con correttezza e semplicità.
Nello schema della tabella
è evidenziato il calcolo di due tassi. Il rapporto tra tassi (Rate Ratio) è
E' utile ricordare due nozioni: - questo RR non deve essere confuso con il Rischio Relativo; il Rate Ratio o rapporto tra tassi ne è solamente una delle misure; - i tassi
Come gli altri
rapporti di rischio, quali i due presentati nei paragrafi precedenti, anche i
rapporti tra tassi
- sia per il calcolo dei limiti di confidenza, - sia per il test di significatività.
Per entrambi, poiché il logaritmo di un rapporto tra due tassi è uguale alla differenza tra i logaritmi dei due tassi
si ricava che
- la varianza di una differenza è uguale alla somma delle due varianze.
Quando un tasso
la varianza
stimata del logaritmo del tasso ( Pertanto, poiché
la varianza
è di
e l'errore
standard di
L'intervallo di
confidenza alla probabilità a del logaritmo vero del rapporto di
due tassi
La significatività del logaritmo del rapporto di due tassi, in un test unilaterale oppure bilaterale con ipotesi nulla H0: r =
1 oppure H0:
può essere verificata con
La stesse ipotesi nulle, che in questo caso sono meglio espresse con H0: dove - m non indica la
media ma è il simbolo greco del tasso
possono essere verificate anche mediante la - significatività
della differenza tra due tassi
con
dove
I valori Z1
e Z2 dei due test di significatività non sono identici.
Dovrebbero essere approssimativamente uguali, in particolare quando i
tassi
FORMULA TEST BASED DI MIETTINEN La deviata normale standardizzata Z1 calcolata per la differenza tra due tassi quindi ottenuta con
serve nella formula test-based di Miettinen
per calcolare i limiti di confidenza del rapporto reale (r) tra tassi, alla probabilità del 95%.
ESEMPIO 1 (RAPPORTO RR E SUOI LIMITI DI CONFIDENZA). Riprendendo i dati del paragrafo precedente con due campioni abbastanza grandi
calcolare 1 - i tassi dei campioni 1 e 2 e il tasso totale; 2 - il rapporto dei tassi (RR); 3 - i limiti di confidenza al 95% del logaritmo del rapporto dei tassi; 4 - i limiti di confidenza al 95% del rapporto vero dei due tassi. (Nella realtà, i tassi sono nettamente minori di quelli qui utilizzati. Spesso sono espressi non in percentuali ma in per-mille o per-diecimila, come attualmente i livelli di mortalità nelle classi giovanili o per cause specifiche che hanno livelli particolarmente bassi).
Risposte. 1 - I tassi dei campioni 1 e 2 e il tasso totale sono
2 - Il rapporto RR tra i due tassi (Rate Ratio) è
3 - Il logaritmo
del rapporto tra i tassi ( è
e i suoi limiti di confidenza al 95% sono - il limite inferiore L1
- il limite superiore L2
4 - I limiti di confidenza al 95% del rapporto vero dei due tassi (con RR = 1,20) sono - il limite
inferiore
- il limite
superiore
ESEMPIO 2 (SIGNIFICATIVITA’ DEL RAPPORTO R, CON DATI ESEMPIO 1). Con gli stessi dati dell’esempio 1, verificare 1 - la significatività del logaritmo del rapporto tra tassi 2 - la significatività della differenza tra tassi
Risposta. 1 - La significatività
del logaritmo del rapporto tra tassi ( H0:
in un test che può essere bilaterale oppure unilaterale è data da
E’ un valore di Z molto piccolo, lontano dai valori critici.
La stessa ipotesi, - formulata in modo differente ma concettualmente identica, - può essere verificata mediante la differenza tra due tassi, sulla base del ragionamento che se due tassi sono tra loro statisticamente differenti dovrebbero essere differenti sia il loro rapporto, sia la loro differenza. I due metodi devono dare lo stesso risultato.
2 – In modo più formale, la significatività
della differenza tra tassi
H0: dove - m non indica la
media, ma è il simbolo greco del tasso
è
Rispetto al metodo precedente, il risultato ha una differenza trascurabile, dovuta agli arrotondamenti.
ESEMPIO 3 (USO DELLLA FORMULA DI MIETTINEN, CON DATI DI ESEMPIO 1). Con gli stessi dato dell’esempio 1, con la formula test-based di Miettinen calcolare - i limiti di confidenza alla probabilità del 95% del rapporto reale tra tassi.
Risposta. Con RR = 1,2 e Z1 = 1,11 mediante
si trovano - il limite
inferiore L1 =
- il limite
superiore L2 =
E’ semplice
osservare che, con i dati dell’esempio 1, intorno al valore medio
campionario
- il limite
inferiore
- il limite
superiore
confermando la corrispondenza tra i due metodi, anche nel rapporto tra due tassi.
|
|||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |