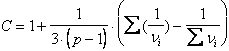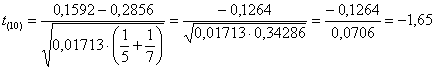INFERENZA SU UNA O DUE MEDIE CON IL TEST t DI STUDENT

 

 

 

6.8.   TEST F, TEST DI BARTLETT E TEST DI LEVENE, PER LA VERIFICA DI IPOTESI BILATERALI E UNILATERALI, SULL’UGUAGLIANZA DI DUE VARIANZE

 

 

Il t di Student è un test di statistica parametrica. In altri termini, è fondato sulle caratteristiche della distribuzione normale, definita appunto da parametri quali la media e la varianza, la simmetria e la curtosi. Affinché possa essere ritenuta valida, l’applicazione del test t di Student richiede

-  che siano rispettate condizioni essenziali, che saranno valide successivamente anche per l’analisi della varianza,  che ne rappresenta la generalizzazione.

Già nel 1947 sulla rivista Biometrics, riferimento fondamentale nello sviluppo della statistica, comparvero in successione tre articoli che illustrano in modo dettagliato tali condizioni:

-  C. Eisenhart (The assumptions underlying the analysis of variances, su Biometrics 1947, vol. 3, pp. 1-21),

- W. G. Cochran (Some consequences when the assumptions for the analysis of variance are not satisfied, su Biometrics 1947, vol. 3, pp. 22-38),

- M. S. Bartlett (The use of transformation, su Biometrics 1947, vol. 3, pp. 39-52).

Le assunzioni di validità di un test parametrico sul confronto tra due o più medie sono essenzialmente tre:

1 -   l’indipendenza dei dati entro e tra campioni;

2 - l’omogeneità della varianza: il confronto tra due o più medie è valido se e solo se le popolazioni dalle quali i campioni sono estratti hanno varianze uguali;

3 - i dati o (detto ancor medio) gli scarti rispetto alla media sono distribuiti normalmente,

 

Con due campioni indipendenti,

-  la assunzione di validità più importante è quella dell’uguaglianza della varianza,

perché rispetto ad essa il test t è meno robusto. Per calcolare la S² pooled, deve essere realizzata la condizione di omoschedasticità o omoscedasticità, cioè che le due varianze siano statisticamente uguali.

I termini  homoscedasticity  e  heteroscedasticity, citati pure come homoskedasticity e eteroskedasticity,  secondo Walker M. H. (vedi, del 1929, Studies in History of Statistical Methods. Williams and and Wilkins, Baltimore, Maryland, 229 pp.) furono introdotti da K. Pearson nel 1905.

 

L'ipotesi di raccolta indipendente dei dati dipende dalla programmazione dell’esperimento. L’ipotesi di normalità dei dati o degli errori (gli scarti dei dati dalla loro media) può essere violata senza gravi effetti sulla potenza del test, a meno di un grave asimmetria; ma

-  l'eguaglianza delle varianze dei due campioni indipendenti dovrebbe essere sempre dimostrata.

 

Nella prassi statistica, fino a poco anni fa il test t di Student per il confronto tra le medie di due campioni indipendenti veniva sempre accettato, se non era più che evidente la loro non omoschedasticità. Ora, da alcuni anni con la diffusione della statistica non parametrica, 

-  si è maggiormente severi nel chiedere il rispetto di questa condizione e

-  si imputa al ricercatore l’obbligo di dimostrare che le due varianze sono statisticamente uguali.

Infatti la varianza associata () è una quantità fondamentale per il calcolo del t e ha significato solamente se è rappresentativa delle varianze di ogni gruppo.

Anche dal punto di vista logico, questo concetto può essere spiegato con semplicità. La varianza è una stima della credibilità di una media: dati molto variabili, quindi con una varianza ampia, a parità del numero di osservazioni hanno medie meno credibili, appunto perché più variabili come i loro dati. Per confrontare due medie, è quindi necessario che la loro “credibilità” sia simile. Sotto l'aspetto tecnico, il problema è che, soprattutto quando i campioni hanno dimensioni molto differenti, una varianza diversa determina la stima della probabilità a e del rischio b che possono essere sensibilmente differenti da quelli nominali o dichiarati.

 

Per l’applicazione del test t, la omoschedasticità tra due gruppi (A e B) è verificata con un test bilaterale, dove l’ipotesi nulla H₀ e l’ipotesi alternativa  H₁ sono

H₀:                H₁:   

E’ possibile anche un test unilaterale, quando una delle due varianze tende a essere sistematicamente maggiore o minore dell’altra. Ma, nella pratica della ricerca ambientale e biologica, in questo contesto di analisi preliminare per il confronto tra le medie di due campioni indipendenti, il test unilaterale è un caso più raro.

I test parametrici più diffusi in letteratura e nelle pubblicazioni per verificare l’omoschedasticità bilaterale o unilaterale sono tre:

A -  il test F o del rapporto tra le due varianze,

B –  il test di Bartlett.

C –  il test di Levene

 

A)   Il test F bilaterale, il primo ad essere proposto e tuttora il più diffuso, è fondato sul

-  rapporto tra la varianza campionaria (s²) maggiore e la varianza campionaria minore:

 

 dove

-   S²_max   è la varianza maggiore,

-   S²_min   è la varianza minore,

-   n_max   è il numero di dati nel gruppo con varianza maggiore,

-  n_min   è il numero di dati nel gruppo con varianza minore.

 

Fondato sull’ipotesi che le due varianze siano uguali (cioè che l’ipotesi nulla H₀ sia vera),

H₀:

-  il rapporto tra esse dovrebbe essere uguale a 1.

Ovviamente è ammessa una certa tolleranza, poiché la stima delle due varianze campionarie non è mai esatta, in particolare quando il campione è piccolo. Solamente quando sono calcolate sulle due popolazioni a confronto, le varianze sono quelle reali. Di conseguenza si ottengono le due s² reali e

- per valutare se  e  sono differenti è sufficiente il semplice confronto, non sussistendo la necessità di ricorrere all’inferenza statistica.

Ma allora anche il test sulla media è inutile, poiché si hanno la due medie vere m_A  e  m_B.

(In merito a questo dibattito, è possibile vedere il concetto di superpopolazione, riportato nell'ultimo capitolo sulla programmazione dell'esperimento).

 

Nella ricerca biologica e ambientale, spesso le varianze sono stimate su campioni di dimensioni molto piccole, formati da poche unità. Di conseguenza, il rapporto tra le due varianze è una stima campionaria, che potrebbe variare

-  da uno a infinito   oppure

-  da uno a zero.

Per non utilizzare entrambe queste misure, che darebbero una informazione del tutto analoga e quindi ridondante, è stata scelta

-  la distribuzione dei valori che è più sensibile alle variazioni: quella da uno a infinito.

Il valore ottenuto dal rapporto deve essere confrontato con una tabella di valori critici.

 

Nella tabella o tavola, come per tutti i test statistici è riportata

-  la probabilità di trovare per caso rapporti uguali o maggiori di quello calcolato,

-  nella condizione che l’ipotesi nulla sia vera.

 

I valori critici della distribuzione F (che è spiegata nel capitolo dell’analisi della varianza e le cui tabelle sono riportate alla fine di quel capitolo) dipendono dai gradi di libertà che, a differenza di quelli del c² e del t, sono due numeri:

 

 

-   =   rappresenta  i gdl del numeratore, riportati nella prima riga della tabella,

-   =   rappresenta i gdl del denominatore, riportati nella prima colonna della tabella.

Solo se si dimostra che l’ipotesi nulla è vera e pertanto che i due gruppi hanno varianze statisticamente uguali, è possibile usare il test t di Student per 2 campioni indipendenti.

 

ESEMPIO 1 (CON IL TEST F). Verificare la omogeneità delle due varianze dell’esercizio precedente, con i dati essenziali per il test t e per la verifica della omoschedasticità riportati in tabella

 

 

 

 

Risposta. La varianza del gruppo A, calcolata su 5 dati, è risultata  = 0,0399.

La varianza del gruppo B, calcolata su 7 dati, è risultata  = 0,1041

Per verificare l’ipotesi nulla

H₀: s²_A = s²_B

 con ipotesi alternativa bilaterale

H₁: s²_A ¹ s²_B

 si deve applicare il test F

Con i dati dell’esempio,

 si ricava F = 2,61 con gdl 6 e 4.

Per ottenere la probabilità a di trovare per caso questa risposta o un rapporto ancora maggiore, aspettandoci 1, si deve ricorrere alle tabelle sinottiche dei valori F di Fisher-Snedecor, dove è presentata l’analisi della varianza.

Nella tabella per la probabilità a = 0.05, all’incrocio tra

-  gdl 6 nella prima riga o del numeratore e

-  gdl 4 nella prima colonna o del denominatore,

 si trova il valore critico F =  6,16.

Il valore calcolato (2,61) con i dati dei due campioni indipendenti è molto minore di quello critico (6,16), riportato nella tabella.

Di conseguenza,

-  poiché la probabilità di trovare per caso un rapporto come quello calcolato è P > 0.05

-  si accetta l’ipotesi nulla: si può affermare che le due varianze sono statisticamente simili.

 

Il test F può essere utilizzato anche per verificare, con un test unilaterale, se una varianza è significativamente minore oppure maggiore di un’altra. Quando si confrontano due reagenti o due strumenti con prove ripetute sullo stesso campione, è migliore quello che ha una varianza minore. In genetica, gli individui che presentano variabilità minore probabilmente hanno un patrimonio genetico più simile oppure vivono in condizioni ambientali più omogenee. Nelle misure d’inquinamento, una variabilità maggiore porta più facilmente a superare i limiti di legge, se i valori medi sono simili.

 

In un test unilaterale sulle varianze,

-  se si vuole verificare che la varianza del gruppo A sia minore di quella del gruppo B,

 si formula l’ipotesi nulla

H₀:

 contro l’ipotesi alternativa

H₁:

 

-  mentre se si pensa che la varianza del campione A sia maggiore di quella del campione B

 l’ipotesi nulla è

H₀:

 e l’ipotesi alternativa

H₁:

 

Per la procedura, il test F unilaterale si distingue da quello bilaterale perché

-  la varianza che si ipotizza maggiore (in H₁) deve sempre essere posta al numeratore.

 

Il motivo è facilmente comprensibile:

- per la significatività, si utilizza la stessa distribuzione F di Fisher,

-  in cui il valore è sempre superiore a 1.

 

Ovviamente, se i dati sperimentali fornissero risultati opposti a quanto ipotizzato in H₁, il test diventa inutile:.

Ad esempio,

-  se  risultasse maggiore di

-  non sarà mai possibile dimostrare H₁ cioè

 e il test diventa inapplicabile o privo di senso.

 

Per verificare l'ipotesi  H₁ cioè ,  il test assume significato solamente se  risulta minore di .

In tal caso serve per verificare

- se la differenza tra esse è trascurabile oppure troppo grande per poter essere ritenuta casuale.

 

 

B)    Il test di Bartlett proposto appunto da

-  M. S. Bartlett nel 1937  con l’articolo Proporties of sufficiency and statistical test (in Proc. R. Soc., A, 160, pp. 268-282),

-  sviluppato e diffuso in particolare da G. W. Snedecor e W. G. Cochran nel loro testo del 1967 Statistical Methods, (6^th ed., Iowa State University Press, Ames)

 dalla sua presentazione ha goduto di tre vantaggi, che hanno favorito la sua diffusione nelle pubblicazioni di statistica applicata:

-  è stato uno dei primi test a essere proposti,

-  non richiede campioni di dimensioni uguali;

- utilizza la distribuzione , i cui valori critici sono riportati su quasi tutti i testi di statistica, per le numerose e importanti applicazioni dei test fondati su di essa.

Per verificare l’ipotesi di omoschedasticità tra due campioni indipendenti,

H₀: s²_A = s²_B

 con ipotesi alternativa bilaterale

H₁: s²_A ¹ s²_B

 utilizza la tavola sinottica

A partire dalle due serie di dati, il valore del  con 1 grado di libertà

 è fondato sul rapporto

 dove

-  C è il fattore di correzione

 

 è determinato da  (il numero di gruppi, in questo caso sempre 2) e  da  (il numero di dati  in ogni gruppo)

 e risulta quasi sempre prossimo a 1:

-  M è uguale a

 

 e dipende da  (la varianza di ogni gruppo) e da   (la media ponderata delle varianze), stimata

 con

 

L’uso più frequente e generale della formula di Bartlett è per più campioni. Per questo motivo, anche se a volte è utilizzata per il confronto tra le varianze di due campioni indipendenti, in questa lunga esposizione dei metodi statistici la sua illustrazione è stata collocata tra i metodi per k campioni, nel capitolo dell’analisi della varianza ad un criterio (vedi indice).

 

 

C)   Il test di Levene è un metodo alternativo; può essere usato anche per integrare l’analisi condotta con il test F, quando si voglia una valutazione più approfondita sull’omogeneità di due varianze.

Ritenuto da vari statistici più robusto del test F rispetto alla non normalità della distribuzione, deve la sua diffusione soprattutto al suo inserimento in alcuni pacchetti statistici.

Per la sua applicazione è necessario disporre dei dati originari, in quanto

-  utilizza gli scarti di ogni valore campionario dal valore centrale del suo gruppo.

 

Del metodo di Levene esistono molte versioni, ma le più diffuse sono tre.

La caratteristica distintiva fondamentale è la misura della tendenza centrale che utilizzano per calcolare gli scarti entro ogni gruppo:

1 -  la media (mean) del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua media

d_i =

 

2 -  la mediana (median) del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua mediana

d_i =

 

3 -  la media trimmed al dieci per cento (ten percent trimmed mean)  del gruppo (), per cui entro ciascun gruppo al posto di ogni singolo dato () si usa la differenza () dalla sua media trimmed

d_i =

In modo più specifico,  per la ten percent trimmed mean si intende la media del gruppo, ma dopo che da esso sono stati eliminati il 10% dei valori maggiori e il 10% dei valori minori.

La scelta del 10% oppure di un’altra qualsiasi percentuale è puramente arbitraria.

La scelta di una tra queste tre misure di tendenza centrale dipende dalla forma della distribuzione.

Si usa

- la media aritmetica, quando la distribuzione dei dati è ritenuta di forma normale, almeno approssimativamente;

- la mediana, quando la distribuzione dei dati è ritenuta asimmetrica;

- la media trimmed quando nella distribuzione dei dati sono presenti valori ritenuti anomali.

(per i concetti di Trimming e Winsorization vedere i paragrafi su gli outlier in statistica univariata)

 

Ma gli scarti rispetto al valore centrale sono sia positivi sia negativi. Per averle tutti positivi, eliminando i segni negativi,

- si elevano al quadrato

d_i =

- oppure sono prese in valore assoluto

d_i =

Il primo metodo è suggerito da pochissimi autori.

Tutti i programmi informatici e quasi tutti gli autori suggeriscono di utilizzare lo scarto in valore assoluto. Tra i due è ovviamente il metodo più potente, in quanto ha una varianza minore entro i gruppi.

 

Per confrontare la varianza di due gruppi (A  e  B),

con ipotesi nulla

H₀: s²_A = s²_B

ed ipotesi alternativa bilaterale

H₁: s²_A ¹ s²_B

la proposta di Levene consiste

-  nell’applicare alla due serie di scarti (in valore assoluto)

-  il test t di Student, nell’assunzione che,

-  se i loro valori medi risultano significativamente diversi, le due varianze dei dati originali sono diverse.

 

Se, utilizzando gli scarti dalla media, si rifiuta l’ipotesi nulla

H₀: m_A = m_B

 per accettare l’ipotesi alternativa

H₁: m_A ¹ m_B

 implicitamente deriva che

 sui dati originali si rifiuta l’ipotesi nulla

H₀: s²_A = s²_B

 per accettare l’ipotesi alternativa

H₁: s²_A ¹ s²_B

Come il test t di Student per due campioni indipendenti, il metodo di Levene per due varianze

- può essere sia bilaterale, sia unilaterale.

 

ESEMPIO. Utilizzando le due serie di dati (A e B), sulle quali in precedenza è stato applicato il test t di Student per verificare la significatività della differenza tra le due medie e il test F per la omoschedasticità, verificare con il test di Levene se hanno varianze significativamente diverse.

 

 

Risposta. Per verificare sui dati l’ipotesi nulla

H₀: s²_A = s²_B

 contro l’ipotesi alternativa bilaterale

H₁: s²_A ¹ s²_B

- si utilizzano gli scarti in valore assoluto

d_i =

 se ovviamente la distribuzione è approssimativamente normale.

E’ accettato l’uso della mediana, ma per la trimmed mean si richiedono campioni numerosi.

Utilizzando programmi informatici, può essere interessante confrontare i differenti risultati.

 

Con i dati della tabella successiva e ricordando che nei dati originari

 

 = 3,994     e      = 3,295

 

 

 

 

 dai dati si ricavano le due serie di scarti in valore assoluto.

Applicando il test alle differenze in valore assoluto , si devono stimare

- le dimensioni dei due campioni

n_A = 5      e      n_B = 7

- le medie degli scarti

 

 

- le devianze degli scarti

 

 

Da esse si calcolano dapprima

 la varianza associata

ed infine il valore di t

 

 che risulta t =  –1,65 con 10 gradi di libertà.

 

Nella tabella dei valori critici, con 10 gdl e per un test bilaterale,

-  alla probabilità a = 0.05 corrisponde un valore di t uguale a 2,228

-  alla probabilità a = 0.10 corrisponde un valore di t uguale a 1,812

-  alla probabilità a = 0.20 corrisponde un valore di t uguale a 1,372

-  alla probabilità a = 0.40 corrisponde un valore di t uguale a 0,879.

Il  risultato t = -1,65 in modulo corrisponde ad una probabilità compresa tra a = 0.10 e a = 0.20. Con un numero così ridotto di dati, con questa probabilità non è certamente possibile rifiutare l’ipotesi nulla, con sufficiente sicurezza.

 

Anche il test di Levene può servire per verificare l’ipotesi unilaterale, cioè

-  l’ipotesi nulla

H₀:

 contro l’ipotesi alternativa

H₁:

 

-  oppure, nell’altra direzione, l’ipotesi nulla

H₀:

 contro l’ipotesi alternativa

H₁:

 

La metodologia illustrata e quelle indicate con la mediana e la trimmed mean sono quelle utilizzate e ritenute appropriate. Tuttavia, per meglio comprendere la logica statistica dei test d’inferenza, è bene evidenziare alcune “anomalie” in questa particolare applicazione inferenziale.

I test statistici sono generalmente impostati per non rifiutare l’ipotesi nulla.

Si rifiuta l’ipotesi nulla, quando esistono evidenze del suo contrario, quindi solo quando

-  si dimostra che la probabilità di trovare per caso differenze grandi come quella riscontrata (o maggiori di essa) è molto piccola.

Se il ricercatore dispone di pochi dati, le differenze tra i due gruppi devono essere molto grandi, perché il test risulti significativo: un test con pochi dati è poco potente, cioè ha probabilità molto basse di rifiutare l’ipotesi nulla, anche quando è noto che essa è falsa.

Ne consegue che, soprattutto in questi casi,

- quando non si rifiuta l’ipotesi nulla H₀, non si può affermare che essa è vera;

- ma solamente che non si è in grado, per la scarsità delle informazioni raccolte, di sostenere che essa è falsa.

 

Il ragionamento è del tutto analogo a quello per un processo. Un individuo non è colpevole, a meno che non esistano evidenze ragionevoli del suo contrario. Quindi, quando non è possibile portare prove della sua colpevolezza, l’individuo è assolto. Ma effettivamente è innocente? Non è dimostrato; solamente non esistono prove della sua colpevolezza, come può avvenire con un’indagine condotta in modo non accurato.

E un test fondato su pochi dati è un’indagine scientifica poco accurata.

 

In termini operativi, è possibile uscire da questo uso illogico dei test per l’omoschedasticità, con una valutazione più completa e dettagliata della probabilità a stimata.

Se, con pochi dati, la probabilità a è di poco superiore a 0.05 (ad esempio 0.10 oppure 0.15) non si può ovviamente rifiutare l’ipotesi nulla. Si parla quindi di significatività tendenziale: se fosse stato possibile disporre di un numero maggiore di dati, con elevata probabilità si sarebbe potuto rifiutare l’ipotesi nulla.

In pratica, secondo vari autori di testi di statistica,

-  si dovrebbe accettare l’ipotesi nulla solo quando la probabilità a calcolata è alta, superiore al 30 per cento; con un numero di dati maggiore, questa probabilità può essere abbassata al 20 per cento.

Purtroppo, per definire un campione grande o piccolo e per decidere a quale livello di probabilità a si possa affermare che l’ipotesi nulla è vera, non esistono regole precise. La scelta è fondata sul buon senso statistico, che può derivare solo dall’esperienza e dalla conoscenza disciplinare di quanto si sta analizzando secondo la metodologia statistica.

 

Con la disponibilità di tabelle che forniscono i valori critici solo per quattro o cinque valori di a, da 0.05 a 0.001, è difficile fare queste valutazioni più complete. Recentemente, con l’uso di programmi informatici, è possibile ottenere dai computer, che dispongono di memoria molto ampia, una stima meno approssimata, della probabilità: quali a = 0.42 oppure a = 0.085 oppure a = 0.64. Solo con il primo (a = 0.42) ed ancor più con il terzo risultato (a = 0.64) sarebbe possibile affermare che le due varianze sono sostanzialmente simili. Con il secondo risultato (a = 0.085) si dovrebbe parlare di tendenziale significatività della differenza tra le due varianze.

Nel caso dell’esempio, è possibile ragionare sul valore di F ottenuto:

-  rispetto al valore critico di 6,16 per a = 0.05, è stato calcolato un valore molto minore (F = 2,61);

-  seppure non stimata con precisione, la probabilità a ad esso associata è alta (forse intorno a 0.50).

Di conseguenza, si può affermare, senza eccessivi timori di essere contestati, che le due varianze sono tendenzialmente simili.

 

Peter Armitage in Statistica Medica (Metodi statistici per la ricerca in Medicina, quarta edizione, marzo 1981 Feltrinelli, Milano, pp. 493; traduzione italiana di Statistical Methods in Medical Research, Blackwell Scientific Publication, 1971) espone una critica esplicita al metodo di Bartlett, estensibile a tutti i test di verifica dell'omogeneità della varianza. Scrive: (a pag. 212) " Il test di Bartlett è forse meno utile di quanto possa sembrare a prima vista; i motivi sono due: il primo è che come il test F è molto sensibile alla non normalità; il secondo è che con campioni di piccole dimensioni le varianze vere devono differire considerevolmente  prima che vi sia una ragionevole probabilità  di ottenere dei risultati significativi. In altri termini, anche se M/C  è non significativo le varianze stimate  e così pure le varianze vere  possono differire in modo sostanziale. Se eventuali differenze delle  hanno peso ai fini delle ulteriori analisi è più saggio ammettere le differenze, anche se il test da un risultato non significativo".