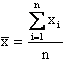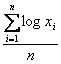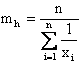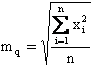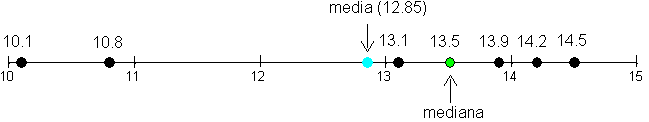elementi di statistica  descrittiva

Per  DISTRIBUZIONI  UNIVARIATe

 

 

1.6.   Le misure di tendenza centrale

 

 

Le rappresentazioni grafiche forniscono una sintesi visiva delle caratteristiche fondamentali delle distribuzioni di frequenza. Rispetto alle cifre, le figure forniscono impressioni che sono percepite con maggiore facilità; ma nel contempo hanno il limite di essere meno precise e meno ricche di particolari.

 

Per i caratteri qualitativi, la tabella e le rappresentazioni grafiche esauriscono quasi completamente gli aspetti descrittivi, quando sia possibile leggere con esattezza le frequenze delle varie classi.

 

Per i caratteri quantitativi, si pone il problema di sintesi oggettive che possano essere elaborate matematicamente e quindi che siano numeriche, al fine di un'analisi obiettiva che deve condurre tutti i ricercatori, con gli stessi dati, alle medesime conclusioni.

 

Una serie di dati numerici è compiutamente descritta da 3 proprietà principali:

1) la tendenza centrale o posizione;

2) la dispersione o variabilità;

3) la forma.

 

Queste misure descrittive sintetiche, riassuntive dei dati tabellari, sono chiamate

-  statistiche, quando sono calcolate su un campione di dati,

-  parametri, quando descrivono la popolazione od universo dei dati.

I ricercatori in ecologia e nelle scienze ambientali molto raramente conoscono tutta la popolazione; di conseguenza, i metodi statistici di norma utilizzati sono riferiti quasi esclusivamente alla descrizione, all’analisi e al confronto di campioni.

 

1.6.1   Le misure di tendenza centrale o posizione servono per individuare il valore intorno al quale i dati sono raggruppati; la tendenza centrale è la misura più appropriata per sintetizzare l'insieme delle osservazioni, se una distribuzione di dati dovesse essere descritta con un solo valore; è la  prima indicazione della dimensione del fenomeno.

Le misure proposte sono essenzialmente 3: la media, la moda e la mediana. Più raramente ed in discipline specifiche si utilizzano altre misure, come l'intervallo medio.

La scelta della misura di tendenza centrale di una serie di dati dipende dalle caratteristiche della distribuzione e dal tipo di scala.

 

La media aritmetica semplice è la misura di tendenza centrale più comunemente utilizzata. Quando si parla solo di media, si intende la media aritmetica semplice. E' definita come la somma del valore di tutte le osservazioni, diviso il numero di unità.

Con simboli, è

 

e, con una notazione più generale, diventa

 dove:

-   = media del campione

-  x_i = i-esima osservazione della variabile X

-  n = numero di osservazioni del campione

-  = sommatoria di tutti gli  x_i  del campione.

 

La media può essere vista come il baricentro della distribuzione campionaria, quando ogni singola osservazione è rappresentata da un peso convenzionale, identico per tutte, lungo l'asse che riporta i valori su una scala di intervalli o di rapporti.

Per dimostrare graficamente che la media aritmetica corrisponde al punto di bilanciamento o di equilibrio dei dati, si supponga di avere 5 misure: 10,9  11,5  12,3  12,8  15,4.

 

La loro media

è uguale a 12,58.

 

La rappresentazione grafica dei dati e della media, riportata nella figura seguente, mostra otticamente come la somma della distanza dalla media dei valori collocati prima sia uguale alla somma della distanza dei valori collocati dopo.

 

 

Figura 15.  Rappresentazione grafica di 5 dati e della loro media aritmetica.

 

In una distribuzione di frequenza raggruppata in classi, come valore rappresentativo di ogni classe è preso il dato centrale, nell’assunzione che, entro ogni classe, i dati siano distribuiti in modo uniforme.

La media aritmetica di distribuzioni di frequenza raggruppate in classi, detta media aritmetica ponderata, è calcolata più rapidamente

 con

 dove:

-     media della distribuzione in classi,

-   x_i =  valore medio della i-esima classe di intervallo,

-   f_i =  numero di osservazioni della classe i-esima classe,

-   n =  numero di classi,                       

-    = sommatoria per tutte le n classi.

 

ESEMPIO.  Da un gruppo di 25 dati, raggruppati nella seguente distribuzione in classi

 

 

 

calcolare la media.

 

Risposta. Con la formula della media ponderata

 

(media)

 

 la media di tutto il campione risulta uguale a 175,4.

 

Le applicazioni della media aritmetica semplice e di quella ponderata sono numerose e derivano da alcune loro proprietà:

- le grandezze additive sono le più frequenti in natura;

- la media aritmetica effettua la correzione degli errori accidentali d'osservazione, per cui essa è la stima più precisa di misure ripetute;

- la media aritmetica è la più semplice delle medie algebriche.

 

Quando le quantità od i fattori causali non sono additivi oppure i dati sono ottenuti da rapporti, si ricorre ad altri tipi di medie; in questi casi, trovano un uso relativamente frequente nelle scienze ambientali la media geometrica, la media armonica e la media quadratica.

 

 

La media geometrica semplice è utilizzata quando le variabili non sono rappresentate da valori lineari, ma ottenuti da prodotti o da rapporti di valori lineari. Serve per il confronto di superfici o volumi, di tassi di accrescimento o di sopravvivenza, per quei valori appunto che sono espressi da rapporti.

Per il calcolo della media geometrica, è condizione necessaria che le quantità siano tutte positive. Se alcune fossero negative, si deve ricorrere al valore assoluto.

La media geometrica di n dati è uguale alla radice di ordine n (solo positiva) del prodotto degli n dati:

con simbologia matematica è

e può essere scritta anche come

 

Una proprietà importante è che

- il logaritmo della media geometrica (log )

 è uguale alla media aritmetica dei logaritmi dei dati   ():

 

 

E’ una proprietà che risulta utile quando si deve ricorrere alla trasformazione dei dati nei loro logaritmi, allo scopo di normalizzare la distribuzione ed applicare in modo corretto i test di inferenza. (Le trasformazioni dei dati sono discusse ampiamente nel capitolo finale dell’analisi della varianza).

 

La media armonica è la stima più corretta della tendenza centrale, per distribuzioni di dati in cui devono essere usati gli inversi. E’ utilizzata quando i valori di X sono espressi come rapporti di un totale costante od in misure di tempi di reazione.

La media armonica è data da

 

 

La media quadratica è la radice quadrata della media aritmetica dei quadrati:

 

 

Sotto l'aspetto matematico può essere calcolata per valori positivi, nulli o negativi; ma essa ha senso come misura di tendenza centrale solamente se i valori sono positivi o nulli. E' un indice che trova applicazioni quando si analizzano superfici.

 

 

1.6.2   La mediana è il valore che occupa la posizione centrale in un insieme ordinato di dati. E’ una misura robusta, in quanto poco influenzata dalla presenza di dati anomali. La sua utilizzazione è indispensabile nel caso di scale ordinali o di ranghi.

La sue caratteristiche più importante sono due:

-  è calcolata sul numero di osservazioni; si ricorre al suo uso quando si vuole attenuare l'effetto di valori estremi o comunque prendere in considerazione solo l’informazione fornita dai ranghi;

-   in una distribuzione o serie di dati, ogni valore estratto a caso ha la stessa probabilità di essere inferiore o superiore alla mediana.

Come la media è la misura di tendenza centrale nella statistica parametrica, la mediana è la misura di posizione o tendenza centrale utilizzata in quasi tutti i test non parametrici.

 

Per calcolare la mediana di un gruppo di dati, occorre

1 - disporre i valori in una fila ordinata in modo crescente oppure decrescente e contare il numero totale n di dati;

2 - se il numero (n) di dati è dispari, la mediana corrisponde al valore numerico del dato centrale, quello che occupa la posizione (n+1)/2;

3 – se il numero (n) di dati è pari, la mediana è stimata utilizzando i due valori centrali che occupano le posizioni n/2 e n/2+1; con poche osservazioni, come mediana viene assunta la media aritmetica di queste due osservazioni intermedie; con molte osservazioni raggruppate in classi, si ricorre talvolta alle proporzioni.

 

ESEMPIO. Calcolare la mediana nella serie di 6 dati: 10,1   10,8   13,1   13,9   14,2   14,5 .

Risposta: Il numero di osservazioni è pari e i due valori centrali sono 13,1 e 13,9; la mediana è individuata dalla loro media aritmetica e quindi è uguale a 13,5.

 

Per meglio comprendere le differenze tra media aritmetica e mediana, con la stessa serie di 6 dati (10,1   10,8   13,1   13,9   14,2   14,5 ) in cui

-  la media è 12,85 e

-  la mediana 13,5 

la rappresentazione grafica evidenzia come la media sia il baricentro della distribuzione e la mediana sia collocata tra i valori più addensati.

 

 

Figura 16.  Rappresentazione grafica della media e della mediana di 6 dati.

 

 

Nella precedente figura 16, il grafico mostra come, nel caso di dati distribuiti in modo non simmetrico, la mediana rappresenti in modo più adeguato della media l’addensamento dei dati, il valore “normale o tipico“ della serie. La media infatti è maggiormente influenzata dalla presenza dei due valori più distanti, che la allontanano dal gruppo dei valori più frequenti e la rendono diversa da essi. Se i due valori anomali fossero più vicini (o più lontani) rispetto agli altri 4, la media cambierebbe mentre la mediana rimarrebbe invariata.

 

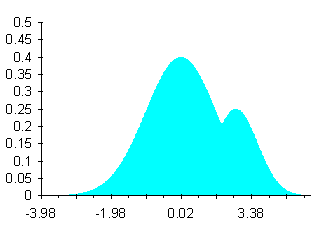
1.6.3   La moda (detta più raramente anche dato prevalente) è il valore più frequente di una distribuzione. Essa non è influenzata dalla presenza di nessun valore estremo; tuttavia viene utilizzata solamente a scopi descrittivi, perché è meno stabile e meno oggettiva delle altre misure di tendenza centrale. Può infatti differire nella stessa serie di dati, quando si formano classi di distribuzione con ampiezza differente. Per individuare la moda entro una classe di frequenza, non conoscendo come i dati sono distribuiti, si ricorre all'ipotesi della uniforme ripartizione.

Oltre alle distribuzioni di frequenza che hanno una sola moda e che si chiamano distribuzioni unimodali, si trovano distribuzioni di frequenza  che presentano due o più mode; sono denominate distribuzioni bimodali o plurimodali.

Le distribuzioni plurimodali possono essere il risultato della scarsità di osservazioni o dell’arrotondamento dei dati; di norma, sono dovute alla sovrapposizione di più distribuzioni con tendenza centrale differente. Per esempio, misurando le altezze di un gruppo di giovani in cui la parte maggiore sia formata da femmine e la minore da maschi si ottiene una distribuzione bimodale, con una moda principale ed una secondaria, come la seguente.

 

 

 

Figura 17.  Distribuzione bimodale

 

 

Quando la distribuzione dei dati evidenzia due o più mode, il ricercatore deve quindi sospettare che i dati non siano omogenei, ma formati da altrettanti gruppi con differenti tendenze centrali. E’ pertanto errato fondare le analisi sulla media generale della distribuzione, poiché non è vera l’assunzione fondamentale che siano dati tratti dallo stesso universo o popolazione con una sola tendenza centrale.

La media di una distribuzione bimodale, formata in quota pari da maschi e da femmine, sarebbe un valore “assurdo” che non descrive né i maschi né le femmine, ma un individuo inesistente, non essendo né maschio né femmina.

 

L'intervallo medio è semplicemente la media aritmetica tra il valore minimo e quello massimo. Ha il grande vantaggio di essere calcolato molto rapidamente, anche con un numero molto elevato di dati. Deve essere utilizzato con estrema cautela e solamente quando non esistono valori erratici o anomali: la presenza di un solo dato che si differenzia sensibilmente da tutti gli altri determina un valore dell'intervallo medio molto distorto, come misura della tendenza centrale.

In questi casi, può essere usata con maggiore correttezza la media interquartile, definita come la media fra il 1° e il 3° quartile, che risente in misura molto più ridotta della presenza di valori estremi.

Nelle scienze che studiano l’ambiente, l'intervallo medio era utilizzato in alcune discipline come la meteorologia. Poteva essere utile nel caso di una serie di dati sulla temperatura, ove non esistono mai valori anomali; infatti supponendo che in una giornata la temperatura minima sia stata di 10 gradi e quella massima di 20 gradi, il calcolo della media è rapidissimo (15) ed il valore si avvicina notevolmente alla media aritmetica, che richiederebbe un numero elevato di osservazioni e un disegno sperimentale accurato.

Per analogia, in meteorologia sovente questo metodo è stato utilizzato anche per il calcolo della precipitazione media mensile. E’ un procedimento criticabile, addirittura errato: in questo caso si tratta di un fenomeno con elevatissima variabilità, con la presenza di valori che possono essere anomali e che influenzano fortemente sia l’intervallo medio che la  media interquartile.

 

Oltre alla media, alla mediana e alla moda, insieme all'intervallo medio e alla media interquartile tra le misure di tendenza centrale può essere ricordata anche la trimedia proposta da Tuckey e calcolata come

T = (Q₁ + 2Q₂+ Q₃)/4

 

dove Q₂ è la mediana, Q₁ e Q₃ sono rispettivamente le mediane della prima metà e della seconda metà dei dati ordinati, detti anche primo e terzo interquartile.

E' un metodo che potrebbe essere utile quando si dispone di materiale molto variabile o con una distribuzione molto asimmetrica. Per esempio, le misure dell'inquinamento atmosferico presentano vari picchi anomali; la tendenza centrale potrebbe essere espressa dalla trimedia di Tuckey. Ma anche questa misura rientra tra le proposte che hanno avuto scarso seguito.

Le misure classiche, presenti in quasi tutte le discipline ed utilizzate senza sollevare obiezioni, sono media (aritmetica), mediana e moda.