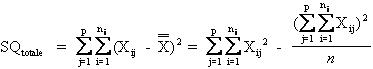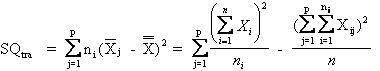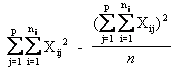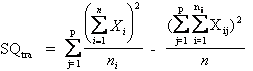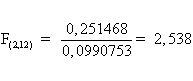|
analisi della varianza (ANOVA I) a un CRITERIO di classificazione E CONFRONTI TRA PIU’ MEDIE
Nella ricerca sperimentale è frequente il confronto simultaneo tra le medie di più di due gruppi, formati da soggetti sottoposti a trattamenti differenti o con dati raccolti in condizioni diverse. Al fine di evidenziare tutte le possibili differenze significative tra le medie, non è corretto ricorrere al test t di Student per ripetere l'analisi tante volte, quanti sono i possibili confronti a coppie tra i singoli gruppi. Con il metodo del t di Student, si utilizza solo una parte dei dati e la probabilità a prescelta per l'accettazione dell'ipotesi nulla, la probabilità di commettere un errore di primo tipo (rifiutare l’ipotesi nulla quando in realtà è vera), - è valida solamente per ogni singolo confronto. Se i confronti sono numerosi, la probabilità complessiva che almeno uno di essi si dimostri significativo solo per effetto del caso è maggiore.
Se è vera l’ipotesi nulla H0, la probabilità che nessun confronto risulti casualmente significativo è (1-a)n dove n è il numero di confronti effettuati. Per esempio, se si effettuano 10 confronti tra le medie di gruppi estratti a caso dalla stessa popolazione e per ognuno di essi a è uguale a 0.05, la probabilità che nessun confronto risulti casualmente significativo diminuisce a circa 0.60 (corrispondente a 0,9510 ). Di conseguenza, la probabilità complessiva che almeno uno risulti significativo solo per effetto di fluttuazioni casuali diventa 0.40. Espresso in termini più formali, effettuando k confronti con il test t di Student ognuno alla probabilità a, la probabilità complessiva a’ di commettere almeno un errore di I tipo (che il test rifiuti l’ipotesi nulla quando in realtà essa è vera) diventa a’ = 1 - (1 -a)k
Nell’analisi della varianza, con apparente paradosso dei termini, il confronto è tra due o più medie. Essa permette il confronto simultaneo tra esse, mantenendo invariata la probabilità a complessiva prefissata.
L'ipotesi nulla H0 e l'ipotesi alternativa H1 assumono una formulazione più generale, rispetto al confronto tra due medie: H0: m1 = m2 = … = mk H1: le mi non sono tutte uguali (oppure almeno una mi è diversa dalle altre; oppure almeno due mi sono tra loro differenti)
La metodologia sviluppata per verificare la significatività delle differenze tra le medie aritmetiche di vari gruppi, chiamata analisi della varianza e indicata con ANOVA dall’acronimo dell'inglese ANalysis Of VAriance, utilizza la distribuzione F. E’ fondata sul rapporto tra varianze, denominato test F in onore di Sir Ronald Aylmer Fisher (1890-1962), giudicato il più eminente statistico contemporaneo e ritenuto il padre della statistica moderna. Nel 1925 Fisher, al quale tra gli argomenti già affrontati si devono la definizione dei gradi di libertà, gli indici di simmetria e curtosi, il metodo esatto per tabelle 2 x 2, completò il metodo di Student per il confronto tra due medie (vedi l’articolo Applications of “Student’s”distribution pubblicato da Metron vol. 5, pp. 90-104). La sua proposta del 1925 (vedi il volume Statistical Methods for Research Workers, 1st ed. Oliver and Boyd, Edinburgh, Scotlnd, pp. 239 + 6 tables) permette di scomporre e misurare l'incidenza delle diverse fonti di variazione sui valori osservati di due o più gruppi. E' la metodologia che sta alla base della statistica moderna; da essa progressivamente sono derivate le analisi più complesse, con le quali si considerano contemporaneamente molti fattori sia indipendenti che correlati. L’evoluzione di questi concetti è descritta anche nella lunga serie del testo di Fisher, fino alla tredicesima edizione del 1958 (Statistical Methods for Research Workers. 13th ed. Hafner, New York, pp. 356).
La metodologia attuale dell’analisi della varianza tuttavia è dovuta a George W. Snedecor (statistico americano, 1881–1974) che con il suo breve testo del 1934 (Calculation and Interpretation of Analysis of Variance and Covariance. Collegiate Press, Ames, Iowa, pp. 96) ne perfezionò il metodo e ne semplificò la forma rispetto alla proposta originale di Fisher. A Snedecor, insieme con W. G. Cochran, è dovuto un altro testo di Statistica che dal 1934 all’ultima edizione del 1980 (vedi Statistical Methods 7th ed. Iowa State University Press, Ames, Iowa, pp. 507) per 50 anni è stato un punto di riferimento fondamentale per tutti gli statistici. La distribuzione F è ricordata anche come distribuzione di Fisher-Snedecor.
La grande rivoluzione introdotta dall’analisi della varianza rispetto al test t consiste nel differente approccio alla programmazione dell’esperimento. L’approccio del test t risente del vecchio assioma che la natura risponde solo a domande semplici. Per organizzare un esperimento, il materiale con il quale formare i gruppi a confronto doveva essere il più omogeneo possibile. Per esempio, per confrontare l’effetto di due tossici su un gruppo di cavie, gli animali dovevano essere dello stesso sesso, della stessa età, della stessa dimensione, ecc., se si riteneva che sesso, età, peso e qualunque altro carattere noto incidessero sulla risposta dell’esperimento. La differenza tra i due gruppi poteva risultare più facilmente significativa, in quanto l’errore standard risultava indubbiamente minore; ma le conclusioni erano ovviamente limitate al gruppo di animali con le caratteristiche prescelte, senza possibilità di estenderle a cavie con caratteristiche differenti. Per rendere più generali le conclusioni, non rimaneva che ripetere l’esperimento, variando un carattere alla volta. Era richiesto un forte aumento della quantità di materiale ed un allungamento dei tempi necessari all’esperimento; alla fine, con tante singole risposte, rimaneva complesso trarre conclusioni generali.
La grande novità introdotta dall’analisi della varianza, come verrà evidenziato progressivamente con analisi sempre più complesse che considerano contemporaneamente un numero sempre più elevato di fattori e le loro interazioni, è la scoperta dei vantaggi offerti all’analisi dall’uso di materiale molto diversificato. Conoscendo le cause ed i diversi fattori, è possibile attribuire ad ognuno di essi il suo effetto e ridurre la variabilità d’errore. Le differenze tra le medie dei gruppi diventano molto più facilmente significative e le conclusioni possono essere immediatamente estese alle varie situazioni. Dall’introduzione dell’analisi della varianza, nella programmazione e realizzazione di un esperimento è vantaggioso usare materiale non omogeneo per tutti i caratteri.
Nell'analisi della varianza, la fonte o causa delle variazioni dei dati viene chiamata fattore sperimentale o trattamento; essa può essere - a più livelli quantitativi, come le dosi crescenti dello stesso farmaco, oppure - a diverse modalità qualitative, come la somministrazione di farmaci differenti.
Ogni unità od osservazione del gruppo sperimentale viene chiamata replicazione o replica; per permettere di calcolare la media e la varianza, ovviamente ogni gruppo deve essere formato da almeno due repliche
10.1. Analisi della varianza ad un criterio di classificazione O A CAMPIONAMENTO COMPLETAMENTE RANDOMIZZATO Il modello più semplice di analisi della varianza, che può essere visto come un’estensione del test t di Student a più campioni indipendenti, è detto ad un criterio di classificazione: ogni dato è classificato solo sulla base del trattamento o del gruppo al quale appartiene. E' chiamato anche modello completamente randomizzato in quanto, soprattutto per analisi di laboratorio, prevede un campionamento in cui gli n individui omogenei sono assegnati casualmente ai vari livelli del fattore. Quando si dispone di un gruppo di soggetti (ad esempio, cavie) da sottoporre a diversi trattamenti per confrontarne gli effetti, l'attribuzione di ogni individuo ad uno specifico trattamento deve avvenire per estrazione casuale da tutto il gruppo. La metodologia di presentazione delle osservazioni, ormai codificata, prevede che i dati sperimentali raccolti siano riportati in modo ordinato secondo la tabella sottostante. Per l'analisi statistica, in questo modello non è richiesto che i vari gruppi abbiano lo stesso numero (ni) di osservazioni o di repliche.
La singola osservazione Xij viene riportata con 2 indici, relativi uno al trattamento o gruppo e l’altro alla posizione occupata entro il gruppo. La media di ogni
gruppo o singolo trattamento La media
generale A partire da queste tre quantità, si stimano le devianze e le varianze utili all’analisi.
L'analisi della varianza è fondata sugli effetti additivi dei vari fattori considerati. Nel modello più semplice, che considera un solo fattore a due o più livelli, ogni singola osservazione Xij può essere scritta come
in quanto determinata - dalla media
generale - dal fattore - da un fattore
casuale (E’ importante ricordare che errore non è sinonimo di sbaglio, ma indica l’effetto di uno o più fattori sconosciuti, comunque non valutati o non controllati nell'esperimento).
Ad esempio, con tre gruppi di persone (A, B, C) alle quali è stata misurata la quantità di una sostanza nel sangue in mg con i seguenti risultati
i dati devono essere letti come se fossero scritti nel seguente modo
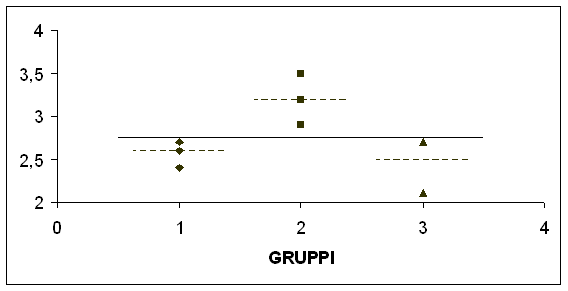
La rappresentazione grafica dei valori osservati illustra con chiarezza ancora maggiore il concetto.
Nella figura, - la riga centrale continua è la media generale, - le tre linee tratteggiate (più brevi) sono le medie dei tre gruppi, - i punti sono le singole osservazioni. I punti riportati appaiono meno numerosi dei dati, perché alcuni valori sono uguali quindi i punti sono sovrapposti. A causa del programma, i gruppi A, B, C nel grafico sono indicati rispettivamente, con 1, 2 e 3.
In tale modello, l'effetto a del trattamento a sua volta è misurato come
dove - mi è la media del
trattamento e Passando dall’enunciazione teorica ai dati sperimentali, si può scrivere che ogni singolo dato Xij di uno specifico trattamento Xij = è determinato - dalla media
generale - dall’effetto del
trattamento ( - da altri fattori non noti, simboleggiati da eij.
Prima dell’applicazione di questo test parametrico, occorre verificare se ne esistono le condizioni. Le assunzioni di validità del test F
dipendono dagli errori - devono essere tra loro indipendenti, - devono essere distribuiti normalmente; inoltre - le varianze dei vari gruppi devono essere omogenee.
L’indipendenza degli errori comporta che la variazione casuale di ogni osservazione non sia influenzata da quella di un'altra: l’errore di una replica, il suo scarto rispetto alla media del gruppo di appartenenza, non deve essere influenzato né dal segno (quando si possono avere valori sia negativi che positivi) né dalle dimensioni del suo valore. A questo fine, la randomizzazione deve essere fondata su elementi obiettivi (effetto random) e non lasciata all’arbitrio o all’intuito dello sperimentatore; ogni dato deve avere la stessa possibilità di essere influenzato dai fattori noti (effetto trattamento) e da quelli ignoti (effetto ambiente statistico). L’attribuzione (che sarà discussa nel capitolo sul campionamento) deve avvenire con modalità indipendenti dal ricercatore.
Gli errori devono essere distribuiti normalmente intorno alla media. Prima dell’applicazione del test deve essere attuato il controllo dell’asimmetria e della curtosi della distribuzione, per verificare che non si discosti eccessivamente dalla normale. Quando lo scostamento è significativo, sovente è possibile ricostruire le condizioni di validità attraverso la trasformazione dei dati (che saranno presentate successivamente).
L’omogeneità della varianza, per cui i diversi gruppi dei quali si confrontano le rispettive medie devono avere tutti la stessa varianza vera (s2), è indispensabile per non determinare perdite nell’informazione sull’effetto dei trattamenti. Anche in questo caso, può essere necessario ricorrere alla trasformazione dei dati. Dopo l’analisi dei dati per la verifica delle condizioni di validità, la metodologia dell'analisi della varianza prevede il calcolo delle seguenti quantità: - la devianza totale, con i suoi gdl; - la devianza tra trattamenti o between, con i suoi gdl e la varianza relativa; - la devianza entro trattamenti o within od errore, con i suoi gdl e la varianza relativa.
Ai fini di una verifica dei risultati e delle successive loro elaborazioni, è utile ricordare che la somma della devianza tra trattamenti e di quella entro trattamenti è uguale alla devianza totale; identica proprietà additiva hanno i rispettivi gradi di libertà.
Devianze, gdl e varianze di un’analisi della varianza abitualmente vengono presentate come nella tabella seguente:
(molti testi riportano la devianza totale e i suoi gdl alla fine, in quanto somma dei precedenti)
La devianza totale o SQ totale (Somma dei Quadrati degli scarti, in inglese SS da Sum of Squares) è calcolato da
La prima è chiamata formula euristica, in quanto definisce il significato della devianza totale: la somma del quadrato degli scarti di ogni valore dalla media generale. La seconda è la formula abbreviata, matematicamente equivalente alla prima, che rende più semplici e rapidi i calcoli necessari. Con essa, la devianza totale è ottenuta come differenza tra la somma dei quadrati di tutti i dati e il quadrato della somma di tutti i dati diviso il numero di dati. La seconda formula ha il vantaggio di richiedere meno operazioni e di non utilizzare la media, che spesso è un valore approssimato; in queste condizioni, consente un calcolo più preciso della formula euristica.
La devianza tra trattamenti ( SQ tra) o between
è per definizione (formula euristica ) la somma dei quadrati degli scarti di ogni media di gruppo dalla media generale, moltiplicato il numero di dati del gruppo relativo. La formula abbreviata utilizza le somme dei gruppi e la somma totale, determinando una maggiore precisione nei risultati.
La devianza entro trattamenti (SQ entro) o within, detta anche errore
è la somma degli scarti al quadrato di ogni valore dalla media del suo gruppo. Per la proprietà additiva delle devianze, può essere ottenuta sottraendo alla devianza totale la devianza tra trattamenti.
I gradi di libertà sono determinati dal numero di somme richieste dal calcolo delle devianze relative, nella formula euristica. - Per la devianza totale, dove la sommatoria è estesa a tutti gli n dati, i gdl sono n-1. - Per la devianza tra trattamenti, dove la sommatoria è estesa ai p gruppi, i gdl sono p-1. - Per la devianza entro od errore, la sommatoria è estesa a tutti i dati entro ogni gruppo. Per calcolare i gdl occorre quindi sottrarre 1 ai dati di ogni gruppo e quindi è determinata da n-p. Per la proprietà additiva dei gdl, può essere scritta anche come (n-1) - (p-1), semplificato in n-p.
Dividendo la devianza tra trattamenti e quella entro trattamenti per i rispettivi gradi di libertà, si ottengono la varianza tra e la varianza entro (la varianza totale è priva d’interesse ai fini di questo test). La varianza fra gruppi misura le differenze esistenti tra un gruppo e l'altro, anche se il calcolo viene attuato rispetto alla media generale. La varianza entro gruppi misura la variabilità esistente attorno alla media aritmetica di ogni gruppo.
Se è vera l'ipotesi nulla, i dati dei vari gruppi sono estratti casualmente dalla stessa popolazione. La varianza tra le medie dei trattamenti e la varianza entro ogni gruppo dipendono dalla variabilità esistente tra i dati: varianza fra (s2F) e varianza entro (s2e) sono due stime indipendenti della stessa varianza vera s2 e quindi dovrebbero avere statisticamente lo stesso valore.
Come indice dell'uguaglianza tra le due varianze, viene utilizzato il test F di Fisher, fondato sul rapporto
varianza-tra / varianza-entro indicato con la simbologia F(p-1,
n-p) =
Se è vera l'ipotesi nulla H0
il rapporto dovrebbe risultare uguale ad 1.
Se è vera l'ipotesi alternativa H1
il rapporto dovrebbe risultare superiore a 1. Il test e la tabella relativa sono unilaterali, appunto perché il valore deve essere maggiore di 1.
Con un numero infinito di trattamenti e di repliche, è sufficiente un rapporto superiore a 1 per rifiutare l'ipotesi nulla (come mostra la tabella dei valori critici di F); con un numero ridotto di dati, il rapporto può essere superiore a 1, per effetto delle variazioni casuali.
I valori critici per i rispettivi gradi di libertà sono forniti dalla distribuzione F. - Se il valore di F calcolato è superiore a quello tabulato, alla probabilità a prefissata, si rifiuta l'ipotesi nulla e si accetta l'ipotesi alternativa: almeno una media è diversa dalle altre. - Se il valore F calcolato è inferiore a quello riportato nella tabella, si accetta l'ipotesi nulla, o almeno non può essere rifiutato che le medie sono tutte uguali.
Valori critici della distribuzione F di Fisher-SnedecorI gradi di libertà del numeratore (o varianza maggiore) sono riportati in orizzontale (prima riga) I gradi di libertà del denominatore (o varianza minore) sono riportati in verticale (prima colonna) a = 0.05 NUMERATORE
Valori critici della distribuzione F di Fisher-SnedecorI gradi di libertà del numeratore (o varianza maggiore) sono riportati in orizzontale (prima riga) I gradi di libertà del denominatore (o varianza minore) sono riportati in verticale (prima colonna) a = 0.025 NUMERATORE
Valori critici della distribuzione F di Fisher-SnedecorI gradi di libertà del numeratore (o varianza maggiore) sono riportati in orizzontale (prima riga) I gradi di libertà del denominatore (o varianza minore) sono riportati in verticale (prima colonna) a = 0.01 NUMERATORE
Valori critici della distribuzione F di Fisher-SnedecorI gradi di libertà del numeratore (o varianza maggiore) sono riportati in orizzontale (prima riga) I gradi di libertà del denominatore (o varianza minore) sono riportati in verticale (prima colonna)
a = 0.005 NUMERATORE
ESEMPIO. Per un controllo della qualità dell'aria, con rilevazioni in tre diverse zone di una città (denominate A, B e C) è stata misurata anche la quantità di ferro (in microgrammi/Nmc a 0°C e 1013 mbar) tra i metalli pesanti in sospensione.
Esiste una differenza significativa tra le tre zone, per la quantità di ferro in sospensione?
Risposta. L’ipotesi nulla H0 è che tra le medie dei tre campioni non esistano differenze significative H0: mA = mB = mC mentre l’ipotesi alternativa H1 H1: le mi non sono tutte uguali.
Attraverso il test F è possibile stimare la probabilità di trovare per caso tra le medie scarti uguali o superiori a quelli sperimentalmente osservati, nell’ipotesi che H0 sia vera.
Come primo passo, dalle tre serie di dati occorre calcolare - il totale di
ogni colonna - il numero di
osservazioni - la media di ogni
colonna
Successivamente, da essi è necessario stimare - la somma totale
- il numero totale di osservazioni n - la media totale
o generale come riportato nella tabella successiva:
A partire da queste quantità, si calcolano le devianze ed i gradi di libertà rispettivi. La devianza totale può essere calcolata dalla somma del quadrato degli scarti di ognuna delle 15 osservazioni rispetto alla media totale, in accordo con la formula euristica
Svolgendo i calcoli e sommando i risultati
si ottiene una devianza totale uguale a 1,691836 con 14 gdl. Questo metodo di procedere al calcolo della devianza totale è lungo e determina stime non precise, quando la media generale è approssimata. Pertanto, per il calcolo manuale è sempre conveniente utilizzare la formula abbreviata SQtotale = che, applicata ai dati dell’esempio,
dalle due diverse somme stima la
devianza totale che risulta uguale a 1,69184.
La corrispondenza tra le due stime è una dimostrazione elementare ed intuitiva dell’equivalenza matematica delle due formule (la differenza tra 1,691836 e 1,69184 è dovuta agli arrotondamenti). La devianza tra trattamenti o between misura la variabilità esistente tra la media aritmetica di ogni gruppo e la media aritmetica generale, ponderata per il numero di osservazioni presenti in ciascun gruppo. Se non esistesse la variabilità casuale ed il valore delle singole osservazioni fosse determinato solamente dal fattore specifico che le raggruppa, le repliche di ogni trattamento dovrebbero avere tutte lo stesso valore ed essere uguali alla media del gruppo, come evidenzia la formula euristica
La devianza tra trattamenti o between è la somma degli scarti di ogni media di gruppo rispetto alla media generale, ponderata per il numero di repliche. Pertanto con la formula euristica il calcolo diventa:
e risulta uguale a 0,503632 con 2 gradi di libertà. Anche in questo caso la formula abbreviata
è più rapida e precisa, non richiedendo le approssimazione determinate dalle medie;
essa risulta uguale a 0,502936. Anche in questo caso le differenze sono minime (0,503632 e 0,502936), imputabili all’uso di un numero diverso di cifre decimali e alle differenti approssimazioni. (Di solito sono sufficienti calcoli con due o tre cifre decimali; il numero più elevato qui utilizzato è motivato dalla necessità contingente di confrontare i risultati dei due metodi).
La devianza entro trattamenti, within od errore
misura la variazione tra il valore di ciascuna replica e la media aritmetica del suo gruppo. Sommando queste differenze elevate al quadrato per ogni gruppo
e sviluppando i calcoli si ottiene
la devianza entro, che risulta uguale a 1,187896 con 12 gdl. La devianza entro od errore può essere ottenuta molto più rapidamente per sottrazione della devianza tra dalla devianza totale, precedentemente calcolate:
Nello stesso modo, per la proprietà additiva, si possono calcolare i gdl: gdl entro = gdl totale - gdl tra = 14 - 2 = 12
Per una presentazione chiara e sintetica, normalmente i valori calcolati sono riassunti in una tabella che riporta le tre devianze, i rispettivi gradi di libertà e le varianze utili al test:
Dividendo la devianza tra e la devianza entro per i rispettivi gradi di libertà, si ottengono la varianza tra e la varianza entro.
Dividendo la
varianza tra per la varianza entro, si calcola il rapporto F, che deve essere
riportato con i rispettivi gradi di libertà
Il valore critico di F con gdl 2 per il numeratore e 12 per il denominatore che è riportato nella tabella per la probabilità a = 0.05 è 3,89. Il valore calcolato (2,538) è inferiore a quello tabulato (3,89): la probabilità che l'ipotesi nulla sia vera è superiore al 5%. Di conseguenza, si accetta l'ipotesi nulla: i tre campioni sono stati estratti dalla stessa popolazione; non esiste una differenza significativa tra le 3 medie campionarie.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||