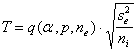ANALISI DELLA VARIANZA a piu’ criteri di classificazione

 

 

11.3.   ANALISI DELLA VARIANZA A TRE O PIU’ CRITERI

 

 

I concetti, le finalità ed i metodi dell’analisi della varianza a due criteri possono essere facilmente estesi a tre o più criteri di classificazione. Con k fattori, è possibile verificare k ipotesi nulle, con altrettante ipotesi alternative bilaterali. A questo scopo occorre calcolare le k varianze, per effettuare  k test F mediante il loro rapporto con la varianza d’errore.

A dimostrazione ed esemplificazione didattica, per facilitare la comprensione dell’analisi della varianza a più criteri di classificazione, vengono di seguito presentati, analizzati e discussi i risultati di un esperimento di genetica ambientale applicata a un problema d’inquinamento, in cui sono stati vagliati contemporaneamente 4 fattori.

 

Per ogni singola osservazione X_ijkp ,  il modello di riferimento diviene

X_ijkp  = m + a_i + b_j + g_k + d_p + R_ijkp

dove

-  m   rappresenta la media generale,

-  a_i ,  b_j ,  g_k ,  d_p   rappresentano gli effetti indipendenti dei 4 fattori, nelle loro varie modalità,

-  R_ijkp   rappresenta tutti gli altri fattori non considerati, sommati alla variazione casuale e agli errori di misura e campionamento, oltre a  tutte le possibili interazioni tra i 4 fattori.

 

Per ognuno dei quattro fattori, si può verificare l’ipotesi nulla

H₀:   tutte le m delle varie modalità dello stesso fattore sono uguali

 contro l’ipotesi alternativa

H₁:   non tutte le m delle varie modalità dello stesso fattore sono uguali

 

Con n osservazioni in ogni modalità, s modalità per ogni fattore ed N osservazioni in totale (N = n×s), la devianza di ogni fattore può essere stimata con la formula euristica o la più rapida formula abbreviata  di seguito riportate

 

 

ESEMPIO.   Si intende verificare se

-          da parte di 4 essenze (medica, plantago, trifoglio, tarassaco),

-          cresciute in 2 località ad alto inquinamento (T₁ e T₂) più un controllo a livelli normali ( C ),

-          esistono differenze nell’assorbimento di 4 metalli (cadmio, nichel, piombo e zinco),

-          considerando anche i 5 sfalci che vengono praticati durante un anno.

Nella pagina successiva sono riportati in tabella i valori unitari per ognuna delle 240 (4 x 3 x 4 x 5) misure campionarie effettuate.

Esistono differenze significative tra le medie di ognuno dei 4 fattori considerati?

 

Risposta.  Per rispondere alle 4 ipotesi nulle che possono essere formulate (una per ognuno dei 4 fattori), applicando le formule già presentate si devono calcolare le devianze, con i rispettivi gdl e le varianze utili ai 4 test F.

I risultati dei calcoli sono riportati nella tabella sottostante, che segue lo schema applicato dai programmi informatici più diffusi.

 

 

 

 

In realtà (come verrà spiegato successivamente nel paragrafo dedicato alla trasformazione dei dati) l’analisi della varianza non può essere applicata direttamente ai valori riportati nella tabella e i risultato dell’analisi precedente è errato. E’ semplice osservare come la distribuzione non sia normale ed esistano grandissime differenze tra le varianze. Ad esempio, risulta del tutto evidente non rispetta le condizioni di validità dell’ANOVA la variabilità presente tra metalli (lo zinco ha valori nettamente superiore agli altri metalli).

L’analisi è effettivamente corretta solamente dopo  la trasformazione di ogni dato (x) nel suo logaritmo naturale o log_e(x).

 

Dopo la trasformazione appena citata, la tabella dell’analisi della varianza risulta

 

 

 

 

- Per valutare la significatività della differenza tra le medie dei 4 metalli contenute nelle 4 essenze, si calcola un rapporto F con gdl 3 e 227

F_(3,227)  =  349,71 / 0,635  =  550,72

 che risulta uguale a 550,7.

 

- Per la differenza tra le medie delle 3 località,

 si calcola un rapporto F con gdl 2 e 227

F_(2,227)  =  1,04 / 0,635  =  1,64

 che risulta uguale a 1,64.

 

- Per la differenza tra le medie delle 4 essenze,

 si calcola un rapporto F con gdl 3 e 227

F_(3,227)  =  3,48 / 0,635  =  5,48

 che risulta uguale 5,48.

 

- Per la differenza tra le medie dei 5 sfalci,

 si calcola un rapporto F con gdl 4 e 227

F_(4,227)  =  1,98 / 0,635  =  3,12

 che risulta uguale a 3,12.

 

Un modo empirico ma corretto (già illustrato in dettaglio nei paragrafi dedicati alle trasformazioni) di valutare l’adeguatezza della trasformazione è dato dal rapporto F, ottenuto per ogni fattore prima e dopo la trasformazione: è migliore la trasformazione che rende complessivamente più significativi i vari test F.

Nelle due tabelle precedenti si può osservare che

-          tra metalli nella prima tabella F risulta uguale a 35,7 contro 550,7 della seconda;

-          tra località nella prima tabella F risulta uguale a 0,777 contro 1,64 della seconda;

-          tra essenze nella prima tabella F  risulta uguale a 1,437 contro 5,48 della seconda;

-          tra sfalci nella prima tabella F risulta uguale a 4,62 contro 3,12 della seconda.

 

E’ evidente la maggiore capacità della trasformazione log_e(x) di ridurre soprattutto la varianza d’errore e quindi di rendere i test F complessivamente molto più significativi (si ha solo una leggera riduzione di F per gli sfalci, contro un aumento grande di quello tra metalli e tra essenze).

 

I calcoli necessari all’esercizio proposto sono lunghi e la probabilità di commettere errori effettuandoli manualmente è alta. E’ quindi necessario ricorrere a programmi informatici. Essi forniscono tutte le informazioni necessarie all’analisi statistica, tra cui il valore di F e la probabilità P relativa, permessa dall’ampia memoria dei calcolatori attuali; nell’analisi dei risultati permettono di superare il limite determinato dal valore approssimato, che si ottiene con il ricorso classico alle tabelle dei valori critici.

Con questa maggiore precisione nelle stima delle probabilità, l’interpretazione può essere più sofisticata.

 

Tra i 4 fattori considerati,

-          due risultano altamente significativi (metalli ed essenze) con probabilità P < 0.001,

-          uno (sfalci) risulta significativo con probabilità P leggermente inferiore al 2% (P = 0.016),

-          il quarto (località) non significativo, avendo una probabilità prossima al 20% (P = 0.196).

 

Insieme con i risultati dell’analisi della varianza, i programmi informatici più sofisticati forniscono anche quelli dei confronti multipli, con vari test relativi ai fattori considerati. Compete al ricercatore scegliere le sole risposte utili al problema. Con i dati dell’esempio, sulla base dell’analisi della varianza che ha permesso di rifiutare l’ipotesi nulla, è interessante verificare tra quali medie dei metalli, delle essenze e degli sfalci la differenza sia significativa: occorre effettuare confronti singoli, per i quali è appropriato il test di Tukey.

 

Nel caso dei metalli, ricordando che si devono effettuare tutti i possibili confronti tra 4 gruppi, nei programmi informatici viene riportato che,

-  alla probabilità a uguale a 0.05, con una varianza d’errore uguale a 0,635 e 60 repliche (n_i) per metallo (dati dal problema),

-  il valore del q studentizzato (Critical Value of Studentized Range) è uguale a 3,660 (fornito dalle tabelle per p = 4 e  gdl =227)

-  applicando la formula già riportata nella presentazione dei confronti multipli a posteriori,

 

 si ottiene

T = 3,660 ×  = 0,3765

 

-          la Differenza Minima Significativa (Minimum Significant Difference), o valore del T, che risulta uguale a 0,3765.

 

I risultati sono riportati sinteticamente in modo grafico nella tabella

 

 

 

 nella quale si evidenzia che alla probabilità a = 0.05

1)  lo Zinco (gruppo A) ha una media significativamente diversa dagli altri 3 metalli,

2)  il Nichel ed il Piombo (gruppo B) hanno medie tra loro uguali ma diverse da quelle degli altri 2,

3)  il Cadmio (gruppo C) ha una media diversa dagli altri 3 metalli.

 

I confronti multipli a posteriori devono essere utilizzati solamente quando l’analisi della varianza permette di rifiutare l’ipotesi nulla alla probabilità prefissata, al fine di non evidenziare con essi differenze significative che non esistono. Tuttavia quasi sempre le conclusioni coincidono.