ANALISI DELLA VARIANZA a piu’ criteri di classificazione
11.5. DATI MANCANTI O ANOMALI IN DISEGNI A PIU’ FATTORI
Nei disegni a blocchi randomizzati e a tre o più fattori, negli esperimenti a quadrati latini e greco - latini, la mancanza anche di una sola osservazione pone vari problemi di elaborazione dei dati. A differenza di quanto avviene nel disegno sperimentale ad un criterio di classificazione o completamente randomizzato, dove l’analisi della varianza non richiede l'eguaglianza del numero di repliche e la perdita di un dato riduce semplicemente il campione di una unità, per cui non è necessario pensare alla sua sostituzione, nei disegni a più criteri è vantaggioso avere un numero rigidamente prefissato e costante di osservazioni, cioè non avere dati mancanti (missing data, missing values), per utilizzare le formule presentate. Nel corso di un esperimento può avvenire che - uno o più dati non possano essere rilevati, come nel caso della morte di una cavia o dell’individuo sul quale il parametro avrebbe dovuto essere misurato, - dopo la rilevazione uno o più dati siano persi, per cancellazione involontaria o smarrimento dell’annotazione, nei vari passaggi richiesti per l’elaborazione statistica, - lo strumento fornisca una o più misure molto approssimate, per le quali non è tarato.
Per sostituire un dato mancante, è fondamentale conoscere la causa della sua non disponibilità, che ai fini statistici può avvenire essenzialmente per 2 motivi: 1) per selezione contro certi valori, che sono troppo grandi o troppo piccoli per essere misurati correttamente dallo strumento a disposizione, 2) per una causa accidentale.
Nella prima situazione (impossibilità di quantificare esattamente uno o più valori, come nella prima e nella terza ipotesi della serie precedente), il campione raccolto è viziato in modo irrimediabile. Non è possibile sostituire in alcun modo le misure mancanti, ma solo indicarle in modo approssimato (superiore a X, inferiore a Y); per la loro analisi è utile ricorrere a test non parametrici. Quando un valore solo è estremamente basso, è accettabile la sua sostituzione con zero oppure la media fra zero e il valore minimo misurabile dallo strumento. Se questi valori sono pochi, rispetto al numero totale di osservazioni, questa procedura è ancora possibile, per l’uso di test parametrici. Ma quando i valori uguali a zero, comunque molto bassi, sono numerosi, la distribuzione dei dati diventa fortemente asimmetrica; quindi per l’inferenza è corretto solo il ricorso a test fondati sul segno o sull’ordine, se la trasformazione dei dati non è in grado di ripristinare le condizioni di validità della statistica parametrica. Quando il valore non è misurabile con precisione perché eccezionalmente alto, sorge una serie di problemi differenti. La distribuzione dei dati diviene asimmetrica e la varianza d’errore molto grande, rendendo i test non più significativi. E’ ovvio che la semplice eliminazione del dato comporti una alterazione dei risultati, in quanto esso è parte effettiva della realtà. Il caso è discusso alla fine del paragrafo.
Nella seconda situazione, quando uno o più valori sono stati perduti o non sono stati rilevati per cause accidentali, è possibile pervenire ad una loro stima. La loro sostituzione è necessaria, per mantenere i campioni bilanciati e quindi utilizzare le formule semplici presentate, pure con correzioni successive. I metodi, le formule e i dati di seguito riportati sono tratti, con alcune integrazioni, dal testo di George W. Snedecor e William G. Cochran del 1967 (Statistical Methods, 6th ed., Iowa State University Press, alle pp. 317-320).
In un disegno a blocchi randomizzati con un solo dato, in cui manchi un valore (single missing observation in a two-way anova without replication), come nella tabella (trattamento D, blocco I)
dopo aver
effettuato le somme (senza il dato mancante), si perviene ad una sua stima (
dove - r = numero di righe o blocchi, - R = totale di riga o blocco senza il dato mancante, - c = numero di colonne o trattamenti, - C = totale di colonna o trattamento senza il dato mancante, - G = totale generale senza il dato mancante.
Per la stima del dato mancante, sono presi in considerazione non solo -
l’effetto
del blocco ( -
l’effetto
del trattamento ( -
media generale ( ma pure il loro numero di osservazioni; inoltre i calcoli sono effettuati sul principio dei minimi quadrati, cioè con lo scopo di ridurre al minimo l’errore. Dai dati della tabella precedente, con r = 5 R = 96,4 c = 4 C = 112,6 G = 627,1 si stima
che risulta uguale a 25,4.
Con questo dato (
ai quali si applicano le formule note dell’analisi della varianza a due criteri di classificazione senza repliche.
Ma l’inserimento di questo valore stimato dagli altri, quindi senza una sua reale informazione, ha indotto alcuni errori sistematici (bias), che devono essere corretti, per un’analisi più precisa. Alle stime dei vari parametri, ottenute con i metodi classici e necessarie per i test di significatività e per il calcolo degli intervalli fiduciali, devono essere apportate le correzioni (in grassetto e con l’asterisco nella tabella successiva), che interessano tre elementi: - i gradi di libertà, - l’errore standard delle medie, - la devianza e la varianza dei trattamenti e dei blocchi.
1) La prima correzione riguarda i gradi di libertà della devianza totale e dell’errore. Poiché il dato inserito è ricavato dagli altri N-1 (19) e quindi non aggiunge un’informazione reale, i gdl della devianza totale sono N-2 (18). Non variano i gdl dei trattamenti e dei blocchi, mentre diminuisce di una unità (11 = 18 –7) il numero di gdl dell’errore, sia perché al dato inserito manca appunto la variabilità casuale o d’errore, sia per la proprietà additiva dei gdl.
2) La seconda correzione concerne il confronto tra le medie di due trattamenti. Quando nessuna delle due medie a confronto è calcolata sul gruppo con il dato mancante, l’errore standard (e.s.) rimane invariato
e.s. = Con -
- r = numero di blocchi (righe) o dati sui quali sono calcolate le medie dei trattamenti (5 nell’esempio) per valutare la significatività della differenza, l’errore standard (e.s.) è 0,795.
Ma quando nel confronto è compresa una media calcolata su un gruppo con il dato stimato, la differenza minima significativa è maggiore di quella precedentemente stimata
e.s. =
e il suo errore standard, con la simbologia precedente e i dati dell’esempio, risulta uguale a 0,859.
3) La terza variazione al metodo generale è la correzione della devianza e/o della varianza sia tra trattamenti sia tra blocchi, per verificare la significatività delle differenze tra le loro medie con il test F. La varianza tra trattamenti e quella tra blocchi, come risultano quando calcolate con il dato inserito (57,12 e 8,85 nella ultima tabella) utilizzando le formule tradizionali, sono maggiori di quelle reali; quindi il test F per la significatività tra le medie dei trattamenti e quello tra le medie dei blocchi in realtà sono meno significativi di quanto risulta da queste stime, ottenute con i valori stimati. Per eliminare questa distorsione (bias), è utile apportare una correzione che, per la varianza tra trattamenti, è data dal valore di A A =
Con i dati dell’esempio, A risulta
uguale a 11,33. Di conseguenza, per la significatività della varianza tra trattamenti con il test F non deve essere utilizzato il valore calcolato (57,12) con le formule generali; ma ad esso occorre sottrarre A, per ottenere il valore corretto (45,79 = 57,12 – 11,33). Il test F tra trattamenti con gdl 3 e 11 è
In altri testi, sempre per la correzione della varianza tra trattamenti, è proposto l’uso non della somma ma della media del blocco, con la formula A = dove -
-
- c è il numero di colonne o trattamenti (4). Ovviamente, essa fornisce risultati identici alla precedente,
A =
come è possibile verificare dal confronto tra le formule e con i dati dell’esempio.
Per la significatività delle differenze tra le medie dei blocchi, alla varianza tra blocchi deve essere sottratta una quantità B B = dove -
-
- r è il numero di righe o blocchi (5).
B =
Pertanto, nella tabella delle devianze e delle varianze, la varianza tra blocchi risulta uguale a 7,34 (8,85 – 1,51) e il test F per la verifica delle differenze tra le medie dei blocchi con gdl 4 e 11 risulta
uguale a 4,645.
Altri testi, quale Biometry di Robert R. Sokal e F. James Rohlf del 1995 (third edition, W. H. Freeman and Company, New York), propongono metodi per correggere le devianze, anche se poi esse perdono la proprietà additiva del modello classico. Per la devianza tra trattamenti si deve stimare un correttore A
A = che con r = 5 R = 96,4 c = 4 C = 112,6 G = 627,1 risulta A = uguale a 35,58 La devianza aggiustata (adjusted) tra trattamenti è quindi uguale a 135,78 (171,36 – 35,58) e la sua varianza è uguale a 45,26 (135,78 / 3), non differente dalla stima precedente (45,79).
Per la devianza tra blocchi si deve stimare un correttore B
B =
Con gli stessi valori usati per il calcolo di A, risulta
B = uguale a 5,86 La devianza aggiustata (adjusted) tra blocchi è quindi uguale a 29,73 (35,59 – 5,86); quindi la varianza aggiustata è uguale a 7,43 (29,73 / 4), non differente dal 7,34 precedente.
Un’altra situazione, riportata con relativa frequenza sui testi, in cui si pone il problema di stimare un valore mancante è il disegno sperimentale a quadrati latini (latin square with one missing value). Il valore mancante
(
dove - k è il numero di dati per fattore o dimensioni del quadrato latino, - R, C, T sono i totali rispettivamente di Riga, di Colonna e del Trattamento (ovviamente, calcolati senza il dato mancante), - G è il totale generale (sempre calcolato senza il dato mancante). Nella tabella a quadrati latini 3 x 3, nella quale in colonna 1 e riga I manca un dato,
dopo aver calcolato i totali di colonna, di riga e dei trattamenti
e quindi con k = 3, R = 1825, C = 1559, T = 1447, G = 6780 il valore stimato
uguale a 511,5 (arrotondato a 512, per avere un valore senza decimali, come gli altri dati).
Con l’inserimento del dato stimato (
(IMPORTANTE: anche se riportato su uno dei testi più classici, l’esempio è finalizzato solamente alla dimostrazione della stima del valore mancante e della correzione della varianza tra trattamenti. In realtà un solo gdl nella varianza d’errore è troppo piccolo, per effettuare un test sufficientemente potente.)
L’errore sistematico (bias), determinato dalla presenza del dato stimato, secondo lo scopo dell’analisi può essere calcolato per la varianza tra righe, la varianza tra colonne e quella tra trattamenti. Limitando la dimostrazione ai soli trattamenti per illustrare i concetti, poiché ora le varianze corrette sono fornite dai programmi informatici, il bias può essere stimato con A =
utilizzando la stessa simbologia e gli stessi dati della formula per il calcolo del dato mancante. Nell’esempio, A risulta A =
uguale a 24.420; di conseguenza, la varianza tra trattamenti corretta risulta uguale a 40.407,5 (64.827,5 – 24.420). Sempre in un quadrato latino di dimensione k x k, l’errore standard della differenza tra le medie di due trattamenti, nei quali non sia compreso il dato mancante, resta e.s. = Quando una delle due medie a confronto (ovviamente, in modo distinto per righe, colonne e trattamenti) è stimata sul gruppo che comprende il dato mancante, l’errore standard della differenza diventa e.s. = Con per due medie calcolate su gruppi diversi da quello del dato sostituito e.s. = l’errore standard risulta uguale a 43,0. L’errore standard della differenza tra due medie delle quali una contenga il dato sostituito, è e.s. = uguale a 56,9.
Quando i dati mancanti sono due o più, la procedura per la loro sostituzione non è più complessa ma più lunga, perché iterativa. Supponendo, per esclusiva comodità di calcolo, di avere un disegno a blocchi randomizzati 3 x 3,
con due valori mancanti (X2,2 e X3,1 ), il metodo richiede alcuni passaggi: 1 – la scelta del primo valore è indifferente, per cui è possibile iniziare a caso da X2,2 ; ad esso si deve attribuire un valore presunto, che non inciderà sul risultato finale, poiché quando è distante dal reale ha il solo effetto di aumentare il numero di iterazioni; 2 – ma poiché è conveniente un valore prossimo a quello che sarà stimato, dato che la media del trattamento al quale appartiene è 11,5 (23/2) e quella del blocco è 10,0 (20/2), in prima approssimazione può essere ragionevole scegliere un valore intermedio tra essi come 10,5; 3 – con l’inserimento di
4 – si calcola il secondo valore mancante (X3,1) con la solita formula
dove r = 3 R = 21 c = 3 C = 27 G = 75,5 ottenendo
un risultato uguale a 17,125;
5 - si inserisce
e quindi con i totali r = 3 R = 20 c = 3 C = 23 G = 82,125 si ritorna a calcolare nuovamente il
valore di
che diventa 11,719;
6 – sostituendo il precedente
e quindi i totali r = 3 R = 21 c = 3 C = 27 G = 76,719 dai quali si perviene a un nuovo valore calcolato per
che risulta uguale a 16,82;
7 – con questo ultimo valore di
e quindi con i totali r = 3 R = 20 c = 3 C = 23 G = 81,82 il nuovo valore calcolato di
diventa 11,795;
8 – questo ultimo valore (X2,2 = 11,795) può essere ritenuto sostanzialmente non differente dalla stima precedente (11,719), data la evidente variabilità dei dati e il loro arrotondamento all’unità; di conseguenza, la tabella definitiva con i due dati calcolati diventa la seguente:
Se l’ultimo valore stimato fosse ritenuto ancora troppo distante dal precedente, si continua l’iterazione che determina valori tra loro sempre più vicini. Per l’inferenza sulle medie dei trattamenti e dei blocchi, alla tabella definitiva è possibile applicare l’analisi della varianza a due criteri di classificazione. Utilizzando, per maggiore semplicità di calcolo, le formula abbreviate,
- la devianza totale (62 + 52 + 42 + 152 + 11,72 + 82 + 16,82 + 152 + 122 ) – (93,52 / 9) = 1.115,84 – 971,36 = 182,77 è uguale a 182,7
- la devianza tra trattamenti (152 / 3) + (34,72 / 3) + (43,82 / 3) – (93,52 / 9) = 75 + 401,36 + 639,48 – 971,36 = 144,48 è uguale a 144,48
- la devianza tra blocchi (37,82 / 3) + (31,72 / 3) + (242 / 3) – (93,52 / 3) = 476,28 + 334,96 + 192 – 971,36 = 31,88 è uguale a 31,88 - la devianza d’errore, ottenuta per differenza 182,77 – (144,48 + 31,88) = 6,41 risulta uguale a 6,41.
Per i test F, la tabella completa con i gdl corretti diventa
Ma, a causa dell’introduzione dei dati stimati, anche in questo caso le devianze tra trattamenti e tra blocchi sono sovrastime del reale; quindi, per un’analisi più precisa, devono essere corrette. Supponendo che il confronto che interessa il ricercatore sia solo quello tra trattamenti, per correggere la sua devianza è necessario:
1 – calcolare la devianza entro blocchi, applicando ai blocchi l’analisi della varianza ad un solo criterio di classificazione, in cui il fattore noto siano i blocchi, con esclusione dei dati inseriti; mediante la formula abbreviata
(6 - 10,5)2 + (15 - 10,5)2 + (5 - 10)2 + (15 - 10)2 + (4 - 8)2 + (8 - 8)2 + (12 – 8)2 = 20,25 + 20,25 + 25 + 25 + 16 + 0 + 16 = 122,5 risulta uguale a 122,5;
2 – essa ha 4 gdl (7 - 3 ) e comprende - sia la devianza tra trattamenti (con 2 gdl) - sia la devianza d’errore (con 2 gdl); di conseguenza, la stima corretta della devianza tra trattamenti è ottenuta sottraendo, a questa ultima devianza entro blocchi (122,5), la devianza d’errore (6,41) calcolata in precedenza nel disegno a due criteri di classificazione; pertanto, la stima corretta della devianza tra trattamenti risulta 122,55 – 6,41 = 116,14 uguale a 116,14 e la sua varianza, avendo 2 gdl, è uguale a 58,07;
3 – il test F con gdl 2 e 2 per la significatività delle differenze tra le medie dei trattamenti è F2,2 =
Ai quadrati latini con due o più dati mancanti sono applicati metodi e concetti simili.
Per i dati anomali, l’approccio è più complesso. Al momento della rilevazione strumentale, dell’annotazione manuale e della sua trascrizione in tabelle o fogli informatici per i calcoli e l’applicazione di test statistici, una misura può essere riportata in modo sbagliato. Ne consegue una varianza d’errore molto grande, che rende il test non significativo e ne pregiudica le condizioni di validità. Occorre quindi verificare attentamente i dati, almeno per comprendere se si tratta di un errore o di un valore effettivo, seppure anomalo o raro rispetto agli altri. Un metodo per individuare questi dati e per valutare la probabilità che il dato appartenga allo stesso gruppo di valori raccolti è fondato sul valore dei loro residui.
Secondo il modello additivo, già presentato per i vari test di
significatività sulle medie, in una analisi della varianza ad un criterio,
con la consueta simbologia il singolo dato ( determinato da
Quindi, l’errore o residuo
In un disegno a blocchi randomizzati senza repliche, la
singola osservazione ( data da
Quindi, il suo errore o residuo
In un quadrato latino senza repliche,
dove la singola osservazione ( data da
e l’errore o
residuo
Snedecor e Cochran nel loro testo citato in precedenza hanno presentato un metodo, proposto da Anscombe e Tukey nel 1963, per valutare se, alla probabilità prefissata, il dato sospetto possa essere ritenuto anomalo nel contesto di tutti quelli raccolti.
Questo metodo è fondato sul valore del residuo R: per definire il dato come anomalo, il residuo deve essere maggiore di una quantità minima
dove -
- C è il risultato di una serie di calcoli, di seguito spiegati nei vari passaggi.
1 – Per il disegno sperimentale in oggetto, è necessario prima calcolare - n = gdl della varianza d’errore - N = numero totale di dati
- Nell’analisi della varianza completamente randomizzata, con gruppi bilanciati, in cui k = numero di gruppi e n = numero di dati per gruppo si ha n = k×(n-1) e N = k×n
- Nell’analisi della varianza a blocchi randomizzati, con r = numero di righe e c = numero di colonne si ha n = (r-1)×(c-1) e N = r×c
- Nell’analisi della varianza a quadrati latini di dimensioni k x k, essi sono n = (k-1)×(k-2) e N = k2
2 – Successivamente stimare a a =
dove P è la probabilità (es.: 0,025 oppure 0,005) alla quale si vuole rifiutare l’ipotesi che il dato in discussione appartenga alla stessa popolazione dalla quale sono stati estratti tutti gli altri
3 - Dal valore di a risalire, con la tabella della distribuzione normale, a quello della deviata normale Z a una coda,
4 – Calcolare H = 1,40 + 0,85×z
5 – Il valore di C è C =
ESEMPIO (per un disegno a blocchi randomizzati). Si supponga che nella tabella a blocchi randomizzati, nella quale in precedenza è stato inserito il valore di 25,4 al posto del dato mancante, successivamente sia stato ritrovato il presunto valore originario e che esso corrisponda a 29,3. La differenza da quello stimato può far sorgere il sospetto che il presunto valore originario sia anomalo. Come stimare la probabilità che esso appartenga effettivamente alla stessa popolazione degli altri 19 dati raccolti?
Risposta 1 - Il primo passo consiste nel calcolare il residuo Rij del dato in discussione. A questo scopo, da tutti i 20 dati della tabella calcolare -
la
media di colonna o trattamento -
la
media di riga o blocco -
la
media generale Attraverso essi, il residuo Rij del valore in discussione (29,3) risulta Rij = 29,3 – 31,425 – 28,38 + 32,82 = 2,315 uguale a 2,315
2 – Sempre dai dati della tabella, si stimano - N = 20 -
la
varianza d’errore
3 – Per rifiutare alla probabilità unilaterale P = 0,025 (perché il residuo più estremo può essere solo dalla stessa parte) l’ipotesi nulla che il dato appartenga alla stessa popolazione delle altre 19 osservazioni, - calcolare a a = che risulta uguale a 0,015.
4 – Ad a = 0,015 in una tabella normale unilaterale corrisponde un valore di Z uguale a 2,17.
5 - Calcolare H che H = 1,40 + (0,85) × (2,17) = 3,24 risulta uguale a 3,24.
6 – Il valore di C C = è uguale a 2,07.
7 – Il residuo minimo significativo alla probabilità P unilaterale prefissata è
uguale a 3,06.
8 – Poiché il residuo di 29,3 è uguale a 2,315 ed esso risulta minore del valore minimo 3,06 calcolato, non è possibile rifiutare l’ipotesi nulla alla probabilità a = 0,05: il valore 29,3 non è significativamente differente dagli altri 19 dati raccolti. Se la verifica delle procedure sperimentali (rilevazione e trascrizione delle misure rilevate) dimostra che il dato indicato come anomalo è effettivamente un errore e non è più possibile risalire al valore reale, è corretto procedere alla sua sostituzione come se fosse un dato mancante. Quando la misura e la trascrizione sono state corrette, è possibile l’uso della statistica parametrica solo se il dato non risulta anomalo, con procedure quale quella indicata; in caso contrario, è bene ricorrere a test non parametrici, che per l’analisi della varianza ad uno e a due criteri di classificazione sono di uso corrente e ormai riportati su tutti i programmi informatici.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
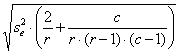 =
= 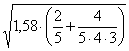 =
= 
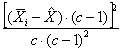
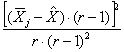
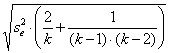
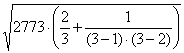 =
= 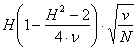
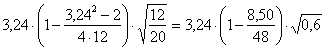 = 2,07
= 2,07