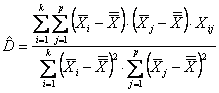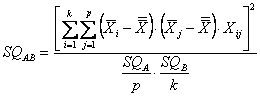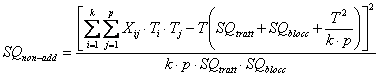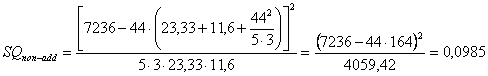analisi FATTORIALE E  disegni complessi

CON FATTORI INCROCIATI

 

 

 

12.8.   TEST DI TUKEY PER LA NON-ADDITIVITA’ CON 1 DF

 

 

Nell’ANOVA a due o a più criteri di classificazione, in varie situazioni non è possibile disporre di repliche, ma di un dato solo per cella. Nel caso più semplice di due soli fattori (A e B), come precedentemente illustrato, il modello additivo o lineare è

X_ij = m + a_i + b_j + R_ij

 dove R_ij ingloba

-          sia la variabilità d’errore vera e propria, comprendente errori di misura, variabilità biologica allo stimolo e soprattutto gli altri fattori non considerati,

-          sia la variabilità d’interazione ab_ij, 

 poiché in questo disegno sperimentale le due diverse quote  non sono tra loro distinguibili mediante i metodi classici, illustrati in precedenza.

Con

-          k livelli dei trattamenti e

-          p livelli dei blocchi,

 la metodologia ANOVA classica permette di scomporre le devianze e i rispettivi gdl secondo lo schema

 

 

Se esiste interazione (), la varianza d’errore () diventa maggiore di quella reale. Ne deriva che più difficilmente con i due test F risultano significative le differenze tra

-          le medie dei trattamenti,

-          le medie dei blocchi.

Soprattutto è in discussione la stessa validità di questi test F, poiché

-          il modello additivo o lineare non è più valido,

-          e/o i residui non sono più distribuiti normalmente.

 

E’ possibile ricostruire le condizioni di validità attraverso la trasformazione dei dati, nella parte finale del capitolo. Ma per una corretta valutazione dei suoi effetti, è necessario quantificare e verificare l’esistenza di questo tipo di interazione prima e dopo la trasformazione effettuata. Si parla perciò di non-additività trasformabile (transformable non-additivity). Se essa persiste anche dopo vari tentativi, eventualmente con l’aiuto del test di Box-Cox per cercare quella più adeguata, è in discussione la validità del test F.

Nel 1949 John W. Tukey (con l’articolo One degree of freedom for non additivity, pubblicato su Biometrics vol. 5, pp. 232-242) propone un metodo che

-          quantifica questa devianza d’interazione,

-          che a 1 df, sottraendolo a quella d’errore.

 

In una ANOVA a due criteri senza repliche, nel caso di interazione il modello diventa

x_ij = m + a_i + b_j + Dab_ij + e_ij

Utilizzando la simbologia consueta, è possibile ottenere una stima dell’interazione , con la formula

 

 

che, seppure nella forma abbreviata, riesce ad evidenziare come l’analisi sia concentrata sugli scarti delle medie di riga e di colonna dalla media generale.

 

Da , si perviene alla devianza d’interazione  con

 

 

Sottraendo alla devianza d’errore  con df (k-1)×(p-1)

-          la devianza d’interazione  con 1 df,

-          si ricava la devianza d’errore rimanente o Residuo  (da Remainder, così chiamata in vari testi; chiamata Balance come da Tukey nell’articolo citato)

I gradi di libertà della  sono (k-1) × (p-1) - 1 = k × p – k - p

 

In questo disegno sperimentale, la tabella completa delle devianze, dei gdl e delle varianze diventa

 

 

(Errore e Remainder sono sinonimi; qui i due termini sono stati distinti, per evidenziare la diversa fonte d’errore che essi indicano,

 

Infine, si verifica se l’interazione è significativa.

In modo più formale, si testa l’ipotesi nulla

H₀: D = 0    (non esiste l’interazione tra i fattori A e B)

 contro l’ipotesi alternativa bilaterale

H₁: D ¹ 0    (esiste interazione tra i fattori A e B)

Con la solita metodologia, avviene con il test F

 cioè il rapporto tra

-          la varianza d’interazione o della non-additivita trasformabile e

-          la varianza remainder o balance,

-          con df che rispettivamente sono 1   e   k×p – k - p

-          per la probabilità a prescelta.

Questa probabilità spesso è superiore a 0.05, potendo ricorre a a = 0.10 oppure a = 0.20.

 

Se il test risulta significativo, è necessario applicare una trasformazione, in modo da annullare o ridurre la devianza d’interazione. Se essa resta significativa, l’ANOVA classica non è valida, comunque ha una potenza molto bassa.

In merito al test di verifica dell’interazione, permangono le perplessità già ripetutamente espresse per i test di omoschedasticità, dove si deve dimostrare che l’ipotesi nulla è vera: non rifiutare l’ipotesi nulla, non significa che essa sia vera.

La scelta conclusiva sulla attendibilità del test è quindi lasciata allo sperimentatore, che meglio conosce l’esistenza o meno della non-additività tra i fattori considerati e quindi sa distinguere tra un risultato accidentale e l’esistenza di un fenomeno reale. Come concetto molto generale, ritorna il problema che non è possibile separare l’analisi statistica dalla conoscenza esatta dello specifico problema ambientale, ecologico o biologico in discussione.

Nel suo articolo del 1949 Tukey ipotizzava che questa tecnica sarebbe stata facilmente estesa ad altri disegni sperimentali più complessi, data l’importanza del concetto di non-additività nelle condizioni di validità dell’ANOVA. In realtà nei testi internazionali a maggior diffusione compare solamente questa applicazione ai blocchi randomizzati; in quasi tutti i programmi informatici neppure questa. E’ quindi una verifica di validità che nella prassi della ricerca è quasi sempre dimenticata, seppure ritenuta importante nelle enunciazioni teoriche.

Gli esempi successivi sono tratti da testi a grande diffusione internazionale. E’ la logica sulla quale è stato costruito questo corso: illustrare in modo semplice ed applicativo le procedure riportate nei testi di riferimento dei rapporti scientifici e delle pubblicazioni internazionali.

 

 

ESEMPIO 1  (CON METODO DI TUKEY).  Nel testo di G. Box, W. Hunter e S. Hunter del 1978 (Statistics for Experimenters. An Introduction to Design, data Analysis and Model Building, John Wiley & Sons, New York, pp. 653) è presentato sinteticamente un esempio che, sviluppato in tutti i suoi passaggi, permette di comprendere la logica del metodo. E’ simile a quello riportato nell’articolo di Tukey, dove sono esposti concetti e metodologia.

 

In un esperimento con 4 trattamenti e 5 blocchi, con i valori osservati  ()

 

 

 

l’ANOVA a due criteri di classificazione ha dato i risultati seguenti

 

 

 

Se non esiste interazione né variabilità casuale, i valori attesi () in ogni casella sono determinati solo dall’effetto dei due fattori considerati; quindi da

 

  e risultano

 

 

 

La differenza tra i precedenti valori osservati () e questi valori attesi  determina i residui

 

 

La somma dei quadrati di questi valori (riportati tra parentesi e in grassetto) corrisponde alla devianza d’errore (), uguale a 226 e con 12 gdl (5-1)×(4-1)

 

La devianza d’errore () è scomponibile in

-          una devianza di non-additività trasformabile () con 1 gdl e

-          una devianza rimanente (remainder o balance) () con 11 gdl.

Per ottenere la devianza della non-additività () si utilizza il quadrato () dei valori attesi () calcolati in precedenza,

 

 

 

 procedendo con essi come è stato fatto con i valori osservati ():

-          prima si calcolano le medie di colonna (), di riga () e totale ()

-          successivamente da esse si ricavano i valori attesi ().

Dalla media di colonna (), di riga () e totale (), attraverso la relazione

 si ottiene una nuova tabella di valori attesi

 

 

Infine quella delle differenze tra le due distribuzioni () e i loro quadrati (tra parentesi)

 

La devianza della non additività è determinata dalle relazioni tra due serie di residui o scarti dai valori medi di riga e di colonna.

La somma di questi ultimi quadrati (tra parentesi e in grassetto) determina il valore Q

Q =  = 3696

La somma del prodotto delle due tabelle dei residui

 

 

 determina il valore di P

P =  = 86

 

Essi permettono di stimare la devianza della non-additività o di interazione SQ_AB attraverso il rapporto

 

La procedura, secondo le parole di Tukey, spiega perché questa devianza abbia solo 1 gdl: è ricavata dal prodotto delle deviazioni dalle medie di riga e dalle medie di colonna, la cui somma deve essere uguale a 0 sia per riga che per colonna, pertanto è 1 gdl ortogonale sia alle righe che alle colonne.

 

La devianza d’errore SQ_e può essere scomposta

-          nella devianza d’interazione o di non additività trasformabile e

-          nella devianza remainder o balance

 

 

 

Infine si deve applicare il test F, per verificare se la varianza della non-additività è significativa

 

In questo caso è inutile, in quanto il rapporto è inferiore a 1 e quindi il suo valore certamente non è significativo.

L’articolo di Tukey illustra anche come la presenza di dati anomali renda significativa la varianza della non-additività e come essa sia nulla quando la distribuzione è perfettamente normale.

 

 

ESEMPIO 2  (FORMULA ABBREVIATA CON MEDIE). Nel testo di John Neter, Michael H. Kutner, Christopher J. Nachtsheim e William Wasserman del 1996 (Applied Linear Statistical Models, 4^th ed. WCB McGraw-Hill, Boston, pp. 1408) è riportato un esempio elementare, più scolastico che reale a causa dei pochi df, ma utile per illustrare la procedura con una formula abbreviata.

In un esperimento con 3 livelli dei trattamenti (A) e 2 livelli dei blocchi (B)

 

 

 l’ANOVA ha dato i seguenti risultati

 

 

In un disegno a due criteri (A e B) aventi k trattamenti e p blocchi, la devianza d’interazione SQ_AB con la formula abbreviata

 

 

 dove con i dati dell’esempio il numeratore è

 

 

 e il denominatore è

SQ_A = 9.300    SQ_B = 1.350    p = 2    k = 3

risulta

uguale a 87,1 con df = 1.

Poiché la devianza d’errore è risultata SQ_e = 100 con df = 2

La devianza remainder SQ_Rem è

100 – 87,1 = 12,9

 uguale a 12,9 con df = 1.

Per verificare l’ipotesi nulla

H₀: D = 0    (non esiste l’interazione tra i fattori A e B)

 contro l’ipotesi alternativa bilaterale

H₁: D ¹ 0    (esiste interazione tra i fattori A e B)

 il testo citato  propone il test F

 che non risulta significativo nemmeno alla probabilità a = 0.10 benché la devianza d’interazione sia quasi 7 volte quella remainder.

Infatti l’esempio riportato in questo testo internazionale ha un numero di gdl troppo ridotto, per una valutazione attendibile dei parametri in gioco.

 

 

ESEMPIO 3 (FORMULA ABBREVIATA CON TOTALE)   Nel testo di Douglas C. Montgomery del 1976 (Design and Analysis of Experiments. John Wiley & Sons, New York, pp. 418) è proposta una formula ancor più rapida, applicata ad un esempio che permette di avere un numero minimo accettabile di df.

 

 

In una rilevazione dei livelli d’inquinamento in 5 località per 3 tempi

 

 

 l’ANOVA ha dato o seguenti risultati

 

 

Per calcolare la devianza della non-additività, con la solita simbologia

 la formula rapida proposta è

 

 

Utilizzando i dati dell’esempio, dopo aver calcolato

 

 si ricava

 

 SQ_non-add = 0,0985

 e infine la devianza remainder

 che risulta SQ_Rem = 1,9015 con df 7.

Per la verifica della significatività della non-additività o interazione, dopo aver calcolato le varianze

 

 

 

 si applica il test F

 che risulta addirittura inferiore a 1. In questo caso, per la verifica della significatività delle differenze tra le medie dei trattamenti e quella dei blocchi è conveniente (avendo una varianza d’errore inferiore e numero di gdl maggiore) , oltre che corretto, utilizzare la procedura classica.