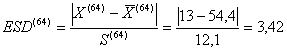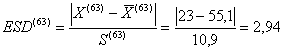trasformazionI dei dati;

test per normalita’ e PER OUTLIER

 

 

 

13.13. la Extreme Studentized Deviate E LA Median Absolute Deviation.

 

 

I  metodi attualmente più diffusi, per identificare gli outliers in un campione di dati, sono

A - un metodo parametrico, la extreme Studentized deviate (ESD) chiamata anche extreme Studentized residuals, che utilizza la media e della deviazione standard del campione,

B - un metodo non parametrico, la median absolute deviation (MAD), che utilizza la mediana e della deviazione mediana assoluta.

 

A - La procedura di statistica parametrica detta Extreme Studentized Deviate (acronomimo ESD) è un altro nome del test di Grubbs, già presentato.

Una dimostrazione elementare di tale corrispondenza è data sia dalle formule, sia dall’uguaglianza dei valori critici, anche se in questo caso il test spesso è presentato come bilaterale bilaterale, mentre in Grubbs era unilaterale. In questo paragrafo sono stati approfonditi i concetti precedenti e il test è stato esteso al caso in cui nello stesso campione siano presenti più outlier.

Il problema della identificazione degli outlier è teoricamente semplice. E’ sufficiente rispondere alla domanda: “Quanto deve distare un valore per essere ritenuto outlier rispetto al campione?”

La risposta deve prendere in considerazione tre fattori:

-  la distanza del dato  dalla media (),

-  la deviazione standard del campione (S),

-  il numero di dati del campione ().

 

Per definizione, la Extreme Studentized Deviate

 è

 considerando che

-  in un campione di  dati,

-  nel quale non siano presenti uno o più outlier,

-  il valore massimo approssimativamente deve corrispondere

 al percentile

Ad esempio,

- in un campione di 60 dati

- estratti da una popolazione distribuita normalmente

-  e quindi senza outlier,

- il valore più alto non dovrebbe distante dalla media più di quanto lo sia

 all’incirca

il percentile 98,36.

Per usare la distribuzione normale, il percentile deve essere tradotto in unità di deviazioni standard  dalla media:

-  in una distribuzione normale bilaterale (vedi tavola della normale bilaterale),

- dal percentile 98,36 si ricava la probabilità dell’area sottesa (0,9836);

- ad essa nelle due code corrisponde  la probabilità bilaterale P = 0,0167 (ricavato da 1 - 0,9836);

- arrotondata a 0.017 determina il valore Z = 2,39.

Pertanto, per essere considerato outlier,

- se è grande deve un dato (X) essere

 maggiore della media di almeno 2,39 volte la deviazione standard.

- mentre se è piccolo un dato (X) deve essere

 minore della media di almeno 2,39 volte la deviazione standard

 

Sempre nell’ipotesi che i dati siano distribuiti in modo normale, per una cautela maggiore e per ottenere una stima più precisa con campioni piccoli, invece della distribuzione Z si può utilizzare la distribuzione t di Student, che tuttavia è specifica solo per la media.

Si ricorrere ai valori critici della tabella successiva (identica alle due precedenti), proposti nel 1961 da C. P. Quesenberry e H. A. David (nell’articolo Some tests for outliers su Biometrika Vol. 48, pp. 379-399) e successivamente modificati.

Le procedure per identificare gli outlier si differenziano sulla base del numero di outlier da verificare:

A₁ -  un singolo outlier,

A₂ -  più outlier.

 

VALORI CRITICI PER

L’EXTREME STUDENTIZED DEVIATE (ESD)

IN OUTLIER STATISTICI PER TEST BILATERALI

 

 

 

A₁ - Per un solo outlier, utilizzando tutto il campione e quindi comprendendo anche il valore sospettato (X), si calcola la media () e la deviazione standard (S).

Successivamente, per verificare l’ipotesi

H₀: non è presente alcun outlier

 contro l’ipotesi

H₁: è presente un valore outlier

 si calcola il valore ESD, che deve essere confrontato con la tabella dei valori critici.

 

ESEMPIO 1.   In un campione di 50 dati ( = 50), la media è  = 56,2 e la deviazione standard è risultata S = 12,3. Il dato più distante dalla media è X = 14,1. Può essere considerato un outlier?

 

Risposta. Per verificare l’ipotesi

H₀: non è presente alcun outlier

 contro l’ipotesi

H₁: è presente un valore outlier

 in un test bilaterale in quanto a priori non era nota in quale coda potesse trovarsi un outlier,

 si calcola il valore di Extreme Studentized Deviate

 

 che risulta ESD = 3,42.

Con N = 50, il valore critico riportato nella tabella

-  alla probabilità a = 0.05 è 3,13

-  alla probabilità a = 0.01 è 3,48.

Poiché il valore calcolato (3,42) è maggiore di 3,13 e minore di 3,48 si può affermare che il valore X è un outlier, con probabilità di sbagliare P < 0.05

 

La procedura illustrata nell’esempio, che non si discosta da quella dei paragrafi precedenti, è corretta quando si ipotizza la presenza di un solo outlier. Ma quando gli outlier sono due o più, la loro presenza amplia notevolmente il valore della deviazione standard  e quindi diventa poco probabile individuare anche un solo valore outlier, poiché con  grande si riduce il valore ESD calcolato.

Questo effetto degli outlier di nascondere la loro presenza è noto come  masking problem.

 

A₂ - In considerazione di questo problema e della probabilità implicata in confronti multipli, nel caso di più outlier, la procedura è più lunga:

-  deve essere applicata quella precedente varie volte, quanti sono gli outlier da verificare,

-  dopo aver prestabilito il loro numero massimo .

Per definire questo numero  di potenziali outlier, il primo problema è che, in rapporto al numero totale di osservazioni del campione, il numero massimo di outlier non deve essere troppo alto, altrimenti si determinano due conseguenze indesiderate:

-  la distribuzione si allontana eccessivamente dalla normalità, quindi il modello utilizzato non è più credibile, 

-  aumenta eccessivamente la varianza, generando il masking effect ricordato.

Una stima giudicata ragionevole (da esperti, ma sempre soggettiva) del numero massimo  di outlier in un campione di  dati deve rispettare due limiti:

1 – è , arrotondando per difetto la parte intera, quando il campione è formato da poche decine;

 ad esempio, con  = 7 sia avrà  quindi

2 – anche se il campione è grande,  non deve mai superare 5, a meno che il campione non sia molto grande, in questo caso superiore almeno a un centinaio di osservazioni;

 ad esempio, con    = 67 sia avrà  quindi .

Come sempre, questi confini non sono definiti in modo preciso, essendo appunto fondati sul “buon senso statistico” o “esperienza statistica”.

 

Nel caso di  outlier (con ), il test serve per verificare

 l’ipotesi nulla

H₀:  non è presente alcun outlier

 contro l’ipotesi alternativa

H₁: sono presenti da  a  outlier

 

La procedura statistica richiede vari passaggi logici, che per comodità didattica sono schematizzati in nove punti.

1 – Dopo aver prestabilito ,

 

2 – sul campione totale di  dati, si calcolano  la media  e la deviazione standard .

Indicando con X⁽ⁿ⁾ il valore più distante dalla media degli  dati, qualunque sia la coda in cui è collocato, si calcola la sua

 Extreme Studentized Deviate con

 

3 – Se si rifiuta l’ipotesi nulla, poiché il valore  calcolato è significativo, dal campione complessivo di  dati, si toglie il valore che è risultato statisticamente un outlier; pertanto il campione diventa di dimensioni .

 

4 - In questo campione successivo di  dati, si calcolano nuovamente

-   la media ^(n-1)

-   e la deviazione standard S^(n-1).

Identificato il nuovo estremo X^(n-1), cioè il valore più distante dalla media in uno dei due estremi della distribuzione, si calcola la sua

Extreme Studentized Deviate con

 

5 – Se anche questo  risulta significativo, dopo aver tolto questo secondo valore, si continua la procedura fino all'ultimo outlier prefissato, che avrà un campione  con  dati;  

 pertanto si ottengono  valori  (al massimo 5)

 che saranno

ESD⁽ⁿ⁾,  ESD^(n-1),  ESD^(n-2), ESD^(n-k+1), ESD^(n-k+1)

 

6 – Successivamente si confronta ESD^(n-k+1), cioè l’ultimo ESD calcolato, con il suo  critico alla probabilità a prefissata e per il numero  di dati del campione.

Se l’ultimo ESD calcolato risulta significativo, tutti i  valori testati sono outlier.

 

7  -  Se  invece questo ESD^(n-k+1)  non risulta significativo,  si confronta il valore  ESD  precedente, cioè ESD^(n-k+2), con lo stesso valore critico precedente per  dati

Se il penultimo ESR risulta significativo, tutti i k-1 valori testati fino a quello (cioè dal primo al penultimo) sono outlier.

 

8 – Se non risulta significativo, si prosegue fino al primo test che risulta significativo. Si dichiareranno outlier sia quel valore, sia tutti i valori precedenti a quello che è risultato significativo.

 

9 – Se anche il primo ESD calcolato, cioè ESD⁽ⁿ⁾, non risultasse significativo, si conclude che nel campione non sono presenti outlier.

 

ESEMPIO 2.   (Tratto, con modifiche, dal testo di Bernard Rosner dell’anno 2000, Fundamentals of Biostatistics, 5^th  ed. Duxbury, Pacific Grove, CA, USA, XIX + 792 p.). 

In campione di 64 dati, ordinati in modo crescente e di cui sono riportati solo gli estremi nelle due code

13,  23,  26,  30,  31,           ,  70,  72,  73,  79,  84

 individuare gli eventuali outliers.

 

Risposta.  Con  = 64, il numero massimo di outlier identificabili sarebbe  = 64/10 = 6.

Ma poiché la parte intera del rapporto  è maggiore di 5, si determina  = 5.

Di conseguenza, supponiamo di voler verificare se nei 64 dati sono compresi 5 outlier, come massimo possibile.

 

Successivamente,

1 – sul campione totale di 64 dati,

-  si calcolano la media  = 54,4 e la deviazione standard  = 12,1 

-  e si individua il valore più estremo X = 13 (in quanto 13 - 54,4 è lo scarto massimo in valore assoluto di tutta la distribuzione).

In questo caso il potenziale outlier è collocato nella coda sinistra della distruzione dei valori, ordinati per rango. Sui 64 dati si calcola la

 prima Deviata Estrema Studentizzata

 

 

2 - Eliminato il valore estremo 13, il campione resta con  = 63 dati. Su di essi

-  si calcolano la nuova media  = 55,1 e la nuova deviazione standard   = 10,9 

-  e si individua il nuovo valore più estremo, che in questo caso è  X = 23 in quanto dista dalla media di questo secondo campione ( = 55,1) più del valore estremo (84) collocato nell'altra coda (ricordare che è un test bilaterale).

Su questi 63 dati, si calcola la

 seconda Deviata Estrema Studentizzata

 

 

3 – Si procede nello stesso modo per gli altri 3 possibili outlier, con il numero  di osservazioni che progressivamente scende da 62 a 60.

I risultati dei vari passaggi, per i = 5 potenziali outlier (), sono riportati nella tabella:

 

 

 

 I 5 valori ESD, nell’ordine con il quale sono stati calcolati, sono:   3,42     2,94     2,90     2,91     2,63.

Si tratta di valutare la loro significativà

 

4 – Nella tabella dei valori critici riportata in precedenza, si individuano i valori teorici massimi per i vari  . Ma sono riportati solamente di valori critici per  = 60  e   = 70; essi sono

- per a = 0.05 con  = 70 il valore ESD critico = 3,26

- per a = 0.05 con  = 60 il valore ESD critico = 3,20.

Mediante interpolazione tra questi due estremi, è possibile calcolare i valori critici per i cinque valori , da 64 a 60.

Per semplicità e come scelta prudenziale, si può assumere come valore critico ESD = 3,26.

Dal confronto emerge che gli ultimi 4 valori ESD sono nettamente minori (anche di 3,20).

Di conseguenza, per essi non si può rifiutare l’ipotesi nulla: nessuno dei 4 valori estremi corrispondenti (79, 84, 26, 23) può essere considerato un outlier.

Risulta significativo solamente il primo valore ESD, quello calcolato per N = 64.

In conclusione, l’unico vero outlier individuato dal test è il valore 13 con probabilità P < 0.05 di commettere un errore di Tipo I.

Nella tabella precedente che sintetizza i risultati, tali concetti sono esposti con P < 0.05 per il primo outlier (X = 13)  e con NS (per Non Significativo) per gli altri 4 valori.

 

 

 B - Una procedura statistica non  parametrica, quindi più robusta della precedente ma meno potente, è la Median Absolute Deviation (acronimo MAD) illustrata anche da P. Sprent nel suo volume del 1998 Data driven statistical methods (London, Chapman & Hall). E’ un metodo che egli giudica semplice e ragionevolmente robusto (a simple and reasonably robust test).

Come il precedente ESD, questo metodo MAD è valido per la scoperta sia di uno solo sia di più outlier.

Per la verifica dell’ipotesi nulla

H₀: non è presente alcun outlier

 contro l’ipotesi alternativa

H₁: sono presenti k valori outlier

 si rifiuta l’ipotesi nulla per ogni specifico outlier

 se

 dove

-   è il valore ritenuto outlier,

-   è la mediana del campione di dati, comprendendo l’outlier,

-   è la deviazione mediana assoluta (in inglese median absolute deviation)

-   è il valore critico, che nella proposta di Sprent è prefissato sempre uguale a 5.

 

MAD è una misura  non parametrica di dispersione o variabilità di una distribuzione di dati, analoga alla deviazione standard . E’ nota da tempo, tanto da essere citata già nell’Ottocento da Johann Karl Friedrich Gauss, il matematico tedesco al quale è attribuita la distribuzione normale. Come caratteristiche statistiche, MAD è ritenuta uno stimatore meno efficiente (sinonimo di meno potente) della deviazione standard . Ma di essa è più robusta, soprattutto con dati distribuiti in modo non normale, benché la sua validità sia crescente all’aumentare della normalità.

Da una distribuzione campionaria di dati, MAD è ricavata calcolando

-  prima la mediana M,

-  successivamente tutte le differenze (D) in valore assoluto di ogni dato (X) dalla loro mediana (M)

- Si ottengono  differenze D.

- A loro volta, esse devono essere ordinate in modo crescente, per ricavare la MAD, che è appunto la mediana di questa serie di differenze.

-  Per la ricerca di  outlier, 

 

 il calcolo di  deve essere ripetuta altrettante volte.

 In questa procedura,

-  varia il valore  che identifica l’outlier,

- mentre restano costanti sia la mediana  sia la , utilizzando sempre quelle calcolate su tutto il campione di  osservazioni.

 

Non esiste una tabella di valori critici, collegati alla probabilità a e al numero  di dati.

Il valore critico di  è uno solo, prefissato uguale a 5 (), secondo l’indicazione di Sprent. Tale scelta deriva

- dalla relazione empirica che esiste tra  e deviazione standard :

- e dal fatto che se una distribuzione dei dati è approssimativamente normale, senza gli outlier, è ragionevole assumere che un dato che dista dalla sua media più di 3 deviazioni standard sia un outlier.

Nel testo di statistica non parametrica del 2001 Applied Nonparametric Statistical  Methods (3^rd ed. Chapman & Hall/CRC, London, XII + 461 ), a pag. 409 P. Sprent e N. C. Smeeton scrivono: The choice of 5 as a critical value is motivated by the reasoning that if the observations other than outliers have an approximately normal distribution, it picks up as an outlier any observations more than about three standard deviations from the means.

 

Quando i dati hanno una distribuzione lontana dalla normalità e di forma ignota, è utile la disuguaglianza di Chebyshev, ripresa nei paragrafi precedenti.

 Con la relazione

 essa permette di stimare

-  la percentuale di osservazioni che cadono entro  deviazioni standard  dalla media.

 

Il confronto tra la percentuale ottenuta con la distribuzione normale e questa percentuale ottenuta per i vari  da 2 a 5 (con 1 non si può calcolare Chebyshev)

 

 

 

 permette di vedere che con  = 5

- quando la distribuzione dei dati è molto lontana dalla normalità, l’errore nel definire un outlier è uguale al 4% (100 - 96);

- mentre se la distribuzione fosse normale, l’errore è minore di 1 uno su centomila.

 

ESEMPIO 3.  (Tratto, con modifiche, dal testo di P. Sprent e N. C. Smeeton del 2001 Applied nonparametric statistical methods,  3^rd ed. Chapman & Hall/CRC, London, IX + 461 p.). 

Nella seguente serie di 11 osservazioni

 

 

 

 verificare se esistono outlier.

 

Risposta. Per verificare l’ipotesi nulla

H₀: non è presente alcun outlier

 contro l’ipotesi alternativa

H₁: sono presenti k valori outlier

 

1 - dapprima si ordinano gli  dati (X) in modo crescente

 

 

 

 per individuare la mediana (M): si ottiene M = 6,9 (in grassetto al centro degli 11 dati ordinati).

 

2 – Successivamente, si calcola la differenza (in valore assoluto) di ognuna delle  osservazioni dalla mediana, cioè D = , ottenendo la seguente serie di  11 differenze

 

 

 

Esempio: la prima D =       e l’ultima  D =  

 

3 - Dopo aver ordinato a sua volta questa serie di D in modo crescente, come nella tabella successiva

 

 

 

 si individua la loro mediana (3,2), definita appunto come la mediana delle differenze, prese in valore assoluto.

E’ il valore della MAD. In questo caso  = 3,2

 

4 – Infine si ritorna all’analisi statistica dei dati originali, per verificare se tra essi esistono outlier.

Poiché l’osservazione più distante dalla mediana ( = 6,9) è X = 29,8 si inizia la ricerca da essa; per tale dato, si stima

 ottenendo un valore  = 7,15.

E’ superiore al valore critico, prefissato in  = 5.

Di conseguenza, si rifiuta l’ipotesi nulla e si conclude che il valore X = 29,8 rappresenta un outlier, con probabilità molto piccola di commettere un errore di Tipo I.

Se il primo valore   calcolato è inferiore a 5, si deve concludere che non esistono outlier.

 

5 – Trovato il primo outlier, si passa a verificare la seconda osservazione più distante dalla mediana ( = 6,9);  nel campione degli  = 11 dati,  risulta X = 22,2.

Utilizzando sempre la mediana e la MAD precedenti, calcolata su tutto il campione di 11 dati,

  questo secondo test

 stima  = 4,78. E’ inferiore a 5.

Se ne deve dedurre che per l’osservazione X = 22,2  non esiste evidenza sufficiente per ritenerla un outlier.

 

6 - La ricerca termina con il primo valore più estremo non significativo.

Con i dati di questo esempio, termina a questo punto e  si traggono le conclusioni generali:

-  il gruppo di 11 osservazioni contiene un solo outlier, esattamente il valore X = 29,8.