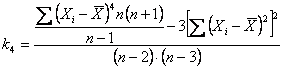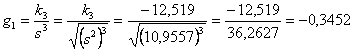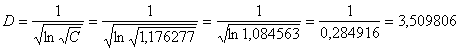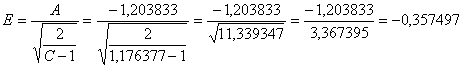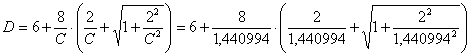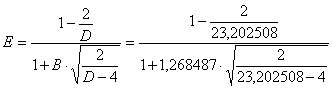|
trasformazionI dei dati; test per normalita’ e PER OUTLIER
13.7. METODI GRAFICI E ALTRI TEST (LILLIEFORS, D’AGOSTINO-PEARSON) PER NORMALITA’, SIMMETRIA E CURTOSI (CENNI DEI TEST DI GEARY E DI SHAPIRO-WILK)
Per analizzare la normalità di una distribuzione, oltre al test c2 i test proposti sono numerosi. Alcuni, ovviamente bilaterali, considerano gli effetti congiunti di asimmetria e curtosi; sono chiamati anche test omnibus (Omnibus test for departure from normality). Attualmente i più utilizzati sono: - il test di Lilliefors, derivato dal test di Kolmogorov-Smirnov chiamato anche distance test, essendo fondato sulla distanza massima tra la distribuzione cumulata osservata e quella cumulata attesa, - il test proposto da R. B. D’Agostino e E. S. Pearson.
Altri test, come già visto nel paragrafo precedente, possono prendere in considerazione solo la simmetria e la curtosi, permettendo anche l’ipotesi unilaterale. Tra questi test possono essere brevemente ricordati - il test di R. C. Geary (vedi gli articoli, entrambi del 1947 e sullo stesso volume, Frequency distribution of Öb1, pubblicato su Biometrika, Vol. 34, pp.: 68-97 e Testing for normality, su Biometrika, Vol. 34, pp.:209-242), - il test di S. S. Shapiro & M. B. Wilks (vedi del 1965 l’articolo An analysis of variance test for normality (complete sample), pubblicato su Biometrika, Vol. 52, pp.: 591-611 e del 1968 l’articolo Approximations for the null distribution of the W statistic, pubblicato su Technometrics, Vol. 10, pp.: 861-866).
Essi non utilizzano i momenti di 3° e 4° ordine, ma un indicatore (U per Geary e W per Shapiro & Wilk) fondato sul rapporto tra le due misure della variabilità. Per Geary U = deviazione media / deviazione standard
Cioè
Calcolato su una popolazione normale, U = 0,7979. Per lo studio delle curtosi, - una curtosi positiva (curva platicurtica) produce valori bassi, inferiori a 0,7979 - una curtosi negativa (curva leptocurtica) produce valori alti, superiori a 0,7979. Il confronto tra i valori di g2 e di U, ovviamente calcolati sugli stessi dati, dimostrano un buon accordo. Il valore U offre due vantaggi - è tabulato anche per campioni di piccole dimensioni, - è più facile e rapido da calcolare. Come quello di Shapiro & Wilk è comunque un test poco diffuso e fondato su una base teorica meno solida.
L’esempio riportato nel paragrafo percedente ha dimostrato che - il test con il c2 ha poca potenza, per verificare la bontà dell’adattamento alla normale di una distribuzione osservata. Questo problema è stato risolto con la richiesta di numero molto alto di osservazioni; ma nella ricerca ambientale e biologica, raramente si raccolgono alcune centinaia di dati. Il test di Kolmogorov-Smirnov, che può essere applicato alla verifica della normalità per un campione, offre il vantaggio di poter essere utilizzato anche con pochi dati. Inoltre, quando la scala è una variabile continua, gli intervalli di classe possono essere molto piccoli e tra loro differenti: ne deriva un’analisi più sensibile, in particolare quando sono importanti le frequenze verso gli estremi.
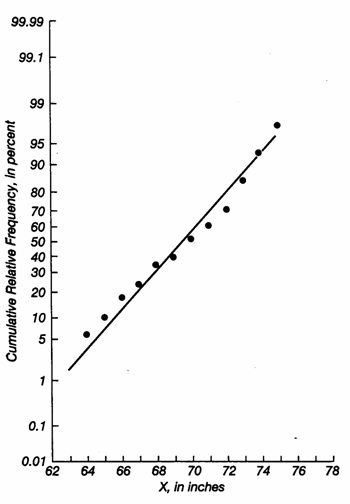
Per analizzare la normalità di una distribuzione, con la diffusione dei computer in questi anni sono stati rilanciati i metodi grafici. Tra essi, è diffuso quello che - sull’asse delle ascisse riporta i valori della scala utilizzata, - sull’asse delle ordinate riporta le frequenza relative cumulate di ogni classe, espresse in percentuale.
Per illustrare questa metodologia, viene riproposta la distribuzione dell’altezza di 70 studenti universitari, misurata in pollici, tratta dal testo di Jerrold Zar del 1999 (Biostatistical Analysis, 4th ed. Prentice Hall, Upper Saddle River, New Jersey):
I valori della X sono distribuiti in modo approssimativamente normale, i punti della percentuale cumulata (Y) sono distribuiti in modo lineare, utilizzando carte specifiche come quella riportata. La pendenza della retta è inifluente, dipendendo solo dalla scala dalla scala delle ascisse.
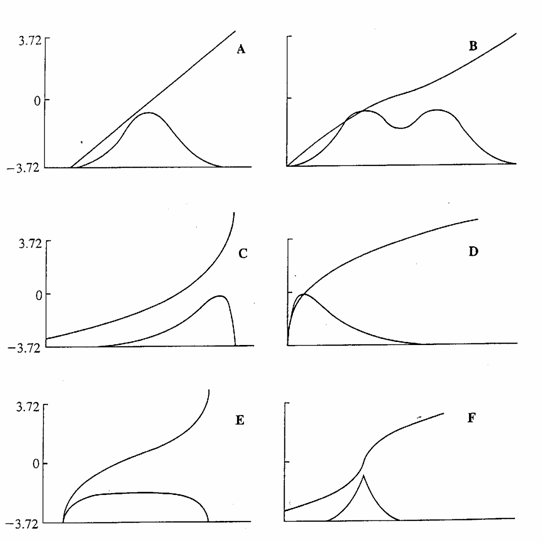
Altri grafici sono più complessi da costruire manualmente perché richiedono il calcolo di Z per tutti i valori campionari di X; ma sono altrettanto semplici da ottenere con il computer. Essi sull’asse delle ordinate riportano il valore di Z, entro un campo di variazione estremamente ampio, che contiene oltre il 99% dei dati. Nelle figure sottostanti, sono riportati schemi grafici in cui il valore di Z varia da –3,72 a +3,72; corrripondono alla percentuali che in ogni coda della distribuzione escludono una frequenza pari a 0.0001 (o 0.01%)
Quando la distribuzione è perfettamente normale (g1 e g2 uguali a 0), la cumulata delle frequenze ha una forma esattamente lineare (Fig. A). I vari tipi di scostamento dalla normalità forniscono curve di forma differente e tipica. Di conseguenza, dalla forma della cumulata è possibile dedurre la probabile forma della distribuzione di frequenza sottostante. Questo metodo risulta più semplice dell’uso della normale, in quanto lo scostamento da una retta risulta visivamente più evidente di quella da una normale, soprattutto quando i dati sono pochi. Nelle altre cinque figure del grafico precedente, sono rappresentate rispettivamente: B) una distribuzione bimodale, C) una distribuzione con asimmetria sinistra (g1 negativo), D) una distribuzione con asimmetria destra (g1 positivo), E) una distribuzione platicurtica (g2 positivo), F) una distribuzione leptocurtica (g2 negativo).
Il test proposto da
H. Lilliefors nel 1967 (vedi l’articolo On the
Kolmogorov-Smirnov test for normality with mean and variance unknown,
pubblicato su Journal of the American Statistical Association Vol. 62,
pp.: 399-402) è particolarmente utile in campioni di dimensioni minime.
I suoi valori critici (vedi tabella nella pagina successiva) iniziano da Come scrive Lilliefors, è una modificazione del test di Kolmogorov-Smirnov: ne segue la procedura, ma utilizza una tavola di valori critici differente. Come in tutti i test di normalità, l’ipotesi nulla è che la popolazione dalla quale è stato estratto il campione non sia troppo differente dalla famiglia di distribuzioni che seguono la legge di Gauss, quindi che sia N (m, s2) con m e s qualsiasi ma g1 = 0 e g2 = 0, contro l’ipotesi alternativa che sia diversa dalla normale a causa di asimmetria e/o curtosi
Dopo aver stimato la funzione di ripartizione della legge normale ridotta N (0, 1), si calcolano - la cumulata delle frequenze attese, nell’ipotesi che la distribuzione sia normale, - la cumulata delle frequenze osservate, - lo scarto massimo tra le due distribuzioni.
La distribuzione dei valori critici è differente da quella di Kolmogorov-Smirnov, poiché la distribuzione normale è calcolata a partire dalla media e dalla varianza campionarie. Oltre al numero di dati, uguale sia nella distribuzione osservata che in quella attesa, sono introdotti due vincoli ulteriori di similarità tra le due distribuzioni a confronto.
Quantili della statistica di Lilliefors per verificare la normalità di una distribuzione campionaria
Si ricorre quindi alla tavola dei quantili di Lilliefors. Se lo scarto massimo calcolato è superiore a quello riportato nella tabella, si rifiuta l’ipotesi nulla: il campione non è stato estratto da una popolazione distribuita secondo la legge di Gauss, ma ha distrosioni dovure ad asimmetria e/o curtosi.
ESEMPIO. Prima di applicare un test inferenziale sulla media delle seguenti 10 misure, si vuole verificare se esse siano state estratte da una popolazione distribuita in modo normale. Per facilitare la procedura, fondata come il test di Kolmogorov-Smirnov (di cui rappresenta una evoluzione) sulla cumulata della distribuzione di frequenza, i valori sono già ordinati per rango
Dopo aver calcolato
la media ( - - per ogni misura
campionaria ( - i valori di Z corrispondenti (riportati nella seconda colonna della tabella successiva)
- la ripartizione delle probabilità della normale ridotta corrispondente
(vedi:
Successivamente, si calcolano - la cumulata
delle probabilità per i valori osservati - e differenze
Per esempio, - la prima D (0,083) è data da 0,083 - 0,000; - la quarta D (-0,037) da 0,363 – 0,400 La differenza massima tra le due distribuzioni è D = 0,137 (nella quinta riga).
Nella tabella dei valori critici di Lilliefors, per n = 10 - alla probabilità a = 0.05 il valore riportato è 0,258 - alla probabilità a = 0.20 è uguale a 0,215. Il valore D calcolato è inferiore anche a questo ultimo. Non è possibile rifiutare l’ipotesi nulla. Inoltre, poiché la probabilità a è maggiore di 0.20, è possibile affermare che lo scostamento della distribuzione campionaria da quella normale; con stessa media e stessa varianza, è trascurabile.
Il test di Lilliefors utilizza la metodologia di Kolgorov-Smirnov. I vincoli, cioè i parametri stimati dal campione sulla base dei quali sono stati calcolati i valori attesi, sono tre - il numero totale di osservazioni, - la media, - la deviazione standard. Non potendo ridurre i gdl come nel c2, si ricorre a valori critici differenti.
Per
Il test proposto da Ralph D’Agostino nel 1971 (vedi articolo An omnibus test of normality for moderate and large size sample, pubblicato su Biometrika, vol. 58, pp.: 341-348), chiamato anche test di D’Agostino–Pearson, per l’articolo di Ralph D’Agostino e E. S. Pearson del 1973 (vedi Test for departure from normality. Empirical results for the distributions of b2 and Öb1, pubblicato su Biometrika, vol. 60, pp. 613-622), appare uno dei test più potenti. (E. S. Perason non deve essere confuso con il più famoso Karl Pearson, che pubblicò nei primi decenni del Novecento) Per l’illustrazione di questo metodo, è stato seguito l’esempio riportato nel volume di Jarrold Zar del 1999 Biostatistical Analysis (4th ed. Prentice Hall, Upper Saddle River, Nee Jersey), uno dei testi classici più diffusi; ad esso si rimanda per approfondimenti. L’ipotesi nulla bilaterale sulla normalità di un campione può essere verificata mediante la statistica
dove - (poiché possono essere sia positivi che negativi, permettono di sommare i diversi tipi di asimmetria e curtosi solo se elevati al quadrato). - K2 è un c2 con 2 gradi di libertà, ricordando la relazione
Il valore di K2 deve quindi essere confrontato con la tabella
che riporta i valori critici del c2 per df = 2 nella coda destra della distribuzione (vedi cap. 3). La procedura di D’Agostino, a partire da una distribuzione di dati, permette di - calcolare g1 e g2, - ricavare da essi Öb1 e b2 - valutare la normalitàsia in complesso, sia indipendentemente gli indici di simmetria e curtosi.
Per illustrare la procedura proposta nel testo di Zar in tutti i suoi passaggi, è stata ripresa la distribuzione di frequenza già utilizzata per la rappresentazione grafica, nella quale non si evidenziava un particolare scostamento dalla normale.
Dai valori delle
classi (
- si ricavano i totali di colonna
Da essi si ottengono: - la devianza (SQ) che con la formula abbreviata
risulta uguale a 755,9429;
- la varianza
(
che risulta uguale a 10,9557;
- il momento
terzo intorno alla media (qui indicato con è
e con la formula abbreviata è calcolato con
risultando con i dati dell’esempio
- il momento
quarto intorno alla media (indicato con è
e con la formula abbreviata diventa
dove
risultando con i dati dell’esempio
Infine si ricavano g1 e g2 con
e
ottenendo
Da queste stime si possono ricavare Öb1 e b2, (che sarebbe stato possibile ricavare direttamente dai dati attraverso m3 e m4). - Da g1 mediante
e con i dati dell’esempio
si ottiene Öb1 = - 0,3378. - Da g2 mediante
e con i dati dell’esempio
si ottiene b2 = 2,2475.
TAVOLA DEI VALORI CRITICI DI
SIMMETRIA APPROSSIMATI ALLA NORMALE PER IL TEST DI D’AGOSTINO
Il test per la simmetria (symmetry) è bilaterale con ipotesi H0: g1 = 0 contro H1: g1 ¹ 0 oppure l’equivalente H0: Öb1 = 0 contro H1: Öb1 ¹ 0 quando di vuole verificare se la distribuzione dei dati raccolti è simmetrica, almeno approssimativamente.
A questo scopo, è sufficiente il semplice confronto del g1 calcolato con i valori critici riportati nella tabella. Con n = 70
e
Ma per - dimensioni campionarie non riportate nella tabella (ma sempre per n ³ 9), sebbene sia possibile un calcolo rapido di interpolazione, e/o - per una stima precisa della probabilità a di ottenere casualmente H0, cioè per non limitarsi a verificare se è maggiore o minore di una probabilità a prefissata, si deve ricavare Zg1, cioè il valore della normale standizzata Z per il valore di g1 calcolato.
A questo scopo, dopo aver ripreso il valore di Öb1 = - 0,337758 già stimato, poiché le formule proposte sono state impostate su di esso, si deve ricorrere a vari passaggi (nei quali è importante avere valori molto precisi, almeno 6 cifre dopo la virgola): - da Öb1 e n si stima A
ottenendo A = 1,203833; - da n si calcola B
ottenendo B = 3,368090; - da B si ricava C
ottenendo C = 1,176277; - da C si ricava D
ottenendo D = 3,509806; - da A e C si ricava E
ottenendo E = -0,357497. Infine da D e E si ottiene Zg1 con
ottenendo Zg1 = -1,2294. Approssimato a Z = -1,23 in una distribuzione normale bilaterale corrisponde ad una probabilità a = 0,219 o 21,9%. E’ una probabilità alta: non solo non permette di rifiutare l’ipotesi nulla, ma autorizza a sostenere ragionevolmente che lo scostamento dalla normale è molto ridotto.
Il test per la simmetria (symmetry) è unilaterale con ipotesi H0: g1 ³ 0 contro H1: g1 < 0 oppure l’equivalente H0: Öb1 ³ 0 contro H1: Öb1 < 0 quando si vuole verificare - se la distribuzione dei dati raccolti ha una asimmetria sinistra o negativa. Il calcolo ha una procedura identica a quella prima illustrata; ma per rifiutare l’ipotesi nulla il valore di g1 deve essere negativo e, in valore assoluto, essere superiore a quello critico.
Si ricorre a un test unilaterale con ipotesi H0: g1 £ 0 contro H1: g1 > 0 oppure l’equivalente H0: Öb1 £ 0 contro H1: Öb1 > 0 quando si vuole verificare - se la distribuzione dei dati raccolti ha una asimmetria destra o positiva. Per rifiutare l’ipotesi nulla, il valore di g1 deve essere positivo e, in valore assoluto, essere superiore a quello critico. Se si ricorre al calcolo di Zg1, per rifiutare l’ipotesi nulla la probabilità a stimata in una distribuzione normale unilaterale deve essere minore di quella prefissata.
Il test per la curtosi (kurtosis) è bilaterale con ipotesi H0: g2 = 0 contro H1: g2 ¹ 0 oppure l’equivalente H0: b2 = 3 contro H1: b2 ¹ 3 quando si vuole verificare - se il campione è stato estratto da una popolazione mesocurtica (normale).
Il metodo più semplice è il confronto con la tabella dei valori critici (pagina successiva). Ad esempio, con n = 70
e
TAVOLA DEI VALORI CRITICI DI CURTOSI
APPROSSIMATI ALLA NORMALE PER IL TEST DI D’AGOSTINO
Anzi, poiché il g2 calcolato è minore, in valore assoluto, di quello riportato nella tabella per la probabilità bilaterale a = 0.20, per quanto rigurda la curtosi si può sostenere che lo scostamento da una perfetta normalità è minimo: la distribuzione è in buon accordo con la normale.
Anche in questo caso, per - dimensioni campionarie non riportate nella tabella (ma sempre per n ³ 20), sebbene sia possibile un calcolo rapido di interpolazione, e/o - per una stima precisa della probabilità a di ottenere casualmente H0, cioè per non limitarsi a verificare se è maggiore o minore di una probabilità prefissata, si deve ricavare Zg2, cioè il valore della normale standizzata Z per il valore di g2 calcolato. A questo scopo,
utilizzando n = 70 e - utilizzando n si calcola A
ottenendo A = 0,277327; - da A e g2 si ricava B
ottenendo B = 1,268487; - utilizzando n si ricava C
ottenendo C = 1,440994; - da C si ricava D
ottenendo D = 23,202508; - da B e da D si ricava E
ottenendo E = 0,648368. Infine da D e da E si ricava Zg2
ottenendo Zg2 = 1,2763. Approssimato a Z = 1,27 in una distribuzione normale bilaterale corrisponde ad una probabilità a = 0,204 o 20,4%. E’ una probabilità alta: non solo non permette di rifiutare l’ipotesi nulla, ma autorizza a sostenere ragionevolmente che lo scostamento dalla normale è molto ridotto. E’ sempre opportuno che l’arrotondamento del valore di Z a due cifre dopo la virgola, come richiesto dalla tabella dei valori critici, avvenga per difetto. Il valore di a è maggiore e il test risulta più cautelativo.
Anche il test per la curtosi può essere unilaterale con ipotesi H0: g2 £ 0 contro H1: g2 > 0 oppure l’equivalente H0: b2 £ 3 contro H1: b2 > 3 quando si vuole verificare specificatamente se la distribuzione dei dati raccolti è platicurtica. Per rifiutare l’ipotesi nulla, il valore di g2 deve essere positivo e, in valore assoluto, essere superiore a quello critico. Con il calcolo di Zg1, per rifiutare l’ipotesi nulla la probabilità a, stimata in una distribuzione normale unilaterale, deve essere minore di quella prefissata.
Per verificare l’ipotesi che la curva sia leptocurtica, cioè con ipotesi unilaterale H0: g2 ³ 0 contro H1: g2 < 0 oppure l’equivalente H0: b2 ³ 3 contro H1: b2 < 3 il valore di g2 deve essere negativo e, in valore assoluto, essere superiore a quello critico. Se si ricorre al calcolo di Zg1 per rifiutare l’ipotesi nulla, la probabilità a calcolata deve essere minore di quella prefissata.
Il test per la normalità, come già presentato all’inizio di questo paragrafo, permette di verificare solo l’ipotesi nulla bilaterale: se il campione è in accordo con la corrispondente distribuzione normale, costruita con stessa media e varianza uguale. Tale test è fondato sulla statistica
e il valore di K2 calcolato deve essere confrontato con la tabella del tabella c2 con df = 2, qui riportata solo nella coda destra della distribuzione:
Con i dati dell’esempio, in cui Zg1 = 1,2294 e Zg2 = 1,2763 mediante
si ottiene K2 = 3,133. Il valore calcolato è nettamente inferiore a quello critico per a = 0.10 (uguale a 4,605). Di conseguenza, la probabilità che l’ipotesi nulla sia vera è alta: c’è sostanziale accordo tra la distribuzione osservata e quella normale corrispondente.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

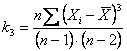
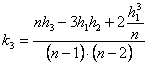
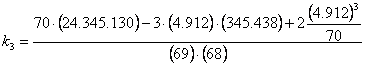 \
\