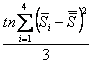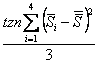L’ANALISI GERARCHICA E

LE COMPONENTI DELLA VARIANZA

 

 

 

14.12.   ANALISI NESTED E PATTERN TEMPORALE

 

 

Lo stesso modello di analisi nested della varianza può essere esteso ai pattern temporali. Apparentemente la programmazione dell’esperimento e l’interpretazione dei risultati sono più facili di quelle per il pattern spaziale e nella ricerca ambientale è utilizzata con frequenza maggiore, per la generalità dello schema delle 4 stagioni; in realtà è più complessa e occorrono maggiori cautele.

Anche su questi argomenti sono stati proposti metodi alternativi, come quello dell’autocorrelazione temporale, che è possibile ritrovare

-  nel volume di J. M. Gottman del 1981 per l’analisi sociale (vedi Time series analysis: a comprehensive introduction for social scientist, edito da Cambridge University Press, Cambridge)

-   e, per un approccio generale, nel testo di G. E. P. Box e G. M. Jenkins del 1976 (vedi Time series analysis: forecasting and control, edito da Holden Day Inc., San Francisco).

 

La maggiore complessità di questa analisi deriva da due fattori: le rilevazioni sono sempre fatte su uno spazio e la misura delle variazioni temporali richiede campionamenti adeguati, che hanno scansioni meno artificiali dello spazio

Non è infrequente il caso in cui un ricercatore effettua alcune rilevazioni nel tempo e raggruppa i dati per stagioni: se con l’anova nested non trova differenze significative tra le loro medie, conclude che non esiste una variabilità temporale. In realtà il ciclo di vita della specie analizzata può essere mensile, settimanale o ancor più breve; all’opposto, una variabilità grande tra periodi è in grado di nascondere l’esistenza di un pattern stagionale che, pure essendo reale, sia meno marcato.

Le repliche spesso sono condotte in località differenti, nelle quali il ciclo di vita della specie studiata ha tempi differenti nelle stagioni. Se nella classificazione per stagioni si sommano i dati delle differenti località, si ottengono valori medi stabili, che non danno risultati significativi, a causa della grande variabilità delle misure entro ogni stagione.

 

Nel volume già citato di A. J. Underwood del 1997 Experiments in Ecology. Their logical design and interpretation using analysis of variance (Cambridge University Press, Cambridge) sono riportati due schemi per l’analisi del pattern temporale dell’abbondanza: il primo quando si utilizza una sola area di campionamento, il secondo quando si vuole tenere in considerazione anche la variabilità spaziale.

 

Nel primo schema di campionamento,

-   per ognuna delle 4 stagioni

-   si effettuano rilevazioni in vari tempi (t), di numero costante per ogni stagione, come può essere una rilevazione mensile o quindicinale,

-  raccogliendo ogni volta un numero costante di repliche (n),

-  per un totale di  osservazioni.

 

Un aspetto importante in questa programmazione dell’esperimento è assicurare che le rilevazioni in tempi successivi nella stessa località non influiscano sulla indipendenza delle osservazioni. In altri termini, non deve succedere che un prelievo, ad esempio di bivalvi, sia così alto da ridurre la densità della popolazione nella rilevazione successiva. Può avvenire in particolare quando la zona di campionamento è troppo piccola rispetto alla quantità del prelievo.

 

Con l’analisi gerarchica della varianza, ovviamente mediante un programma informatico, si ottiene la tabella di risultati

 

 

 

Nei livelli sia tra stagioni sia tra tempi, l’ipotesi nulla è che non vi siano differenze tra le medie delle unità campionate,

H₀: m₁ = m₂ = … = m_k

 rispetto al livello successivo (da I a III),

 mediante il test F,

 ovviamente con i df  relativi.

 

In questo caso, con i dati campionari descritti, iniziando dall’errore le componenti della varianza ai vari livelli sono

(3)     

(2)      +

(1)      +  +

 dove

-    e    indicano rispettivamente la media della stagione e la media generale.

 

Nel secondo schema di campionamento, quando i prelievi sono effettuati in zone differenti

-  per ognuna delle 4 stagioni

-  si effettuano rilevazioni in vari tempi (t) di numero costante per ogni stagione,

-  nelle zone (z) prescelte

-  raccogliendo ogni volta in ogni zona un numero costante di repliche (n),

-  per un totale di  osservazioni.

 

Per una visione complessiva dell’analisi, è utile riportare i risultati in una tabella

 

 

 

La verifica dell’ipotesi nulla sulle medie di ogni livello,

H₀: m₁ = m₂ = … = m_k

 equivalente a quella sulla varianza

H₀ :

 con relativa ipotesi alternativa

H₁:

 è effettuata mediante il solito test F

 

Le componenti della varianza ai vari livelli sono stimati risolvendo

 (4)    

(3)         +

(2)     +  +

 

(1)      +  +  +

 dove, ovviamente, al posto di s deve essere utilizzata la varianza calcolata ai vari livelli.