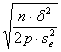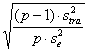L’ANALISI GERARCHICA E

LE COMPONENTI DELLA VARIANZA

 

 

 

14.6.   POTENZA DEL TEST NELL’ANALISI FATTORIALE E IN NESTED ANOVA I

 

 

Nel capito IX è stato presentato il metodo per calcolare la potenza a priori (n) e a posteriori (1-b) in un’ANOVA, con il metodo grafico proposto da E. S. Pearson e H. O. Hartley nel 1951 (vedi l’articolo Charts for the power function for analysis of variance tests, derived from the non-central F-distribution, pubblicato su Biometrika, vol. 38, pp. 112-130).

Sono state presentate le sue applicazioni all’ANOVA a un criterio con vari esempi e le formule per estenderle al disegno sperimentale a due fattori crossed, sia con una sola osservazione sia con più osservazioni per cella. In questo ultimo caso, è stata indicata la metodologia

-   per stimare la potenza dei due test F per gli effetti principali,

-   e la potenza del test F che verifica la significatività delle interazioni.

 

E’ stato presentato come nella programmazione di un esperimento, utilizzando i risultati di uno studio pilota,  si possano stimare

-  la differenza minima (d) che sarà possibile evidenziare;

-  il numero minimo di dati (n) che è necessario raccogliere per ogni gruppo o il numero totale (N) di dati, ovviamente suddiviso in campioni bilanciati poiché fornisce la potenza massima;

-  il numero massimo di gruppi (p) che è utile formare con il numero totale (N) già determinato.

 

 

Con la solita simbologia (p,  ,  n ) e con la procedura precedentemente illustrata in vari esempi, è possibile calcolare la differenza minima significativa (d) attraverso il rapporto

 

d =

 

 dopo avere identificato il valore richiesto di f nel grafico, sulla base dei 4 parametri n₁,  n₂,  a,  1-b.

 

Sono ricavabili

-  sia il numero minimo di dati (n) che è necessario raccogliere

-  sia il numero massimo di gruppi (p) che è possibile formare,

attraverso il grafico, dopo aver calcolato f in modo iterativo secondo la procedura dettagliatamente descritta nel cap. IX. Il valore di f è ottenuto dal rapporto

.

f =

 

Per calcolare la potenza a posteriori (1-b)  di un qualsiasi esperimento, si ricorre alla formula generale

f =

 

 che può essere più operativamente scritta dopo i calcoli dell’ANOVA come

 

f =

 ricordando che

-   è la varianza del fattore che interessa, con p medie a confronto e n₁ gdl (per la scelta del grafico), riportata al numeratore nel test F per la significatività,

-   è la varianza riportata al denominatore e n₂ sono i suoi gdl (per la scelta della curva), nello stesso test F.

 

Nel caso di due criteri di classificazione con n_ij osservazione per cella, occorre distinguere tra

1)       effetti principali

2)       interazione.

 

Per gli effetti principali, il metodo è identico a quello dell’analisi a due criteri con una sola osservazione.

Per l’interazione, il valore di f

è

f =

 

In una Nested ANOVA I o a effetti fissi è possibile applicare le stesse procedure., ponendo attenzione al fatto che i valori cambiano in ogni test F.

In generale,

-   k diviene il numero di gruppi del fattore o livello preso in esame,

-  n è il numero di dati di ogni gruppo (in esperimenti bilanciati; in caso contrario il problema si complica, come discusso nei confronti multipli)

-  al numeratore è riportata la varianza ( ,  ) del fattore oppure quella d’interazione () di cui si vuole verificare la potenza,

-  al denominatore è riportata la varianza (  ) che è stata posta al denominatore anche nel relativo test F, come descritto nei paragrafi precedenti.