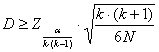TEST NON PARAMETRICI

PER PIU' CAMPIONI

 

 

15.11.   I  CONFRONTI MULTIPLI TRA MEDIE DI RANGHI NELL’Analisi della varianza NON PARAMETRICA, a due criteri di classificazione

 

 

Anche nell’analisi della varianza non parametrica a due criteri di classificazione, dopo aver rifiutato l’ipotesi nulla i confronti multipli permettono di individuare quali sono i trattamenti che risultano tra loro differenti, alla probabilità a prefissata.

In altri termini, per le mediane di due generici gruppi A e B è possibile verificare l’ipotesi nulla

H₀: 

 contro l’ipotesi alternativa bilaterale

H₁: 

 

 

Sulla base dei concetti del Bonferroni già illustrati nelle pagine dedicate ai confronti multipli a posteriori, quando si devono effettuare più confronti mantenendo costante la probabilità complessiva (a_T) o experiment-wise, la singola probabilità (a) di ogni differenza o comparison-wise deve diminuire in rapporto al numero di confronti che si vogliono effettuare.

 

Con k gruppi, i confronti possibili, tra loro non indipendenti,

 sono

Se la probabilità scelta come experiment-wise complessivamente è  a_T = 0.05, per ogni singolo confronto la probabilità a diventa

 

Poiché si considerano le differenze in valore assoluto, questi confronti sono bilaterali. Di conseguenza, la probabilità a per ogni confronto deve essere dimezzata, diventando

 

a  = 

 

Come ampiamente illustrato nel capitolo relativo ai confronti multipli, la stima della probabilità a comparison-wise ha avuto tante soluzioni differenti, che non portano sempre a risultati coincidenti, seppure spesso simili.

 

In questo paragrafo sono riportate le proposte divulgate da Sidney Siegel e N. John Castellan jr. Nel loro volume del 1988 Nonparametric Statistics for the Behavioral Sciences (edito da McGraw-Hill, Inc.) tradotto in italiano nel 1992 con Statistica non parametrica (2° ed., McGraw-Hill Libri Italia, Milano), essi propongono l’uso della distribuzione normale poiché, con i ranghi, sono sufficienti poche decine di osservazioni per ottenerla.

Quando il numero di dati e di gruppi è sufficientemente grande, si può ricorrere alla distribuzione normale applicata alla differenza

-          tra le somme dei ranghi di due gruppi,

-          tra le medie dei ranghi di due gruppi.

 

 

Sono significative le differenze D tra le somme dei ranghi del generico gruppo A (R_A) e del generico gruppo B (R_B)

 quando

 dove:

-  a  è la probabilità complessiva prefissata,

-  k  è il numero di gruppi, tra i quali sono possibili /2 confronti,

-  N  è il numero di righe od osservazioni per ogni campione.

 

 

Sono significative le differenze D tra le medie dei ranghi del generico gruppo A () e del generico gruppo B ()

 quando

 

All’aumentare del numero di confronti, il valore di a per ognuno di essi diventa sempre minore. Ne deriva che non è sempre facile trovare nella distribuzione normale l’esatto valore di Z, quando il numero di confronti è alto: con a molto piccolo, la stima diventa approssimata. In vari testi sono quindi proposte tabelle con stime precise, sulla base del valore della probabilità experiment-wise (a_T) e del numero di confronti (p) che si vogliono effettuare.

 

Nella tabella sono riporti solamente i valori di Z per a_T relativamente grandi.

 

 

VALORI DI Z PER CONFRONTI MULTIPLI

IN FUNZIONE DI a_T E DEL NUMERO P DI CONFRONTI

 

 

Con 4 gruppi tutti i possibili confronti sono 6

Con 5 gruppi tutti i possibili confronti sono 10

Con 6 gruppi tutti i possibili confronti sono 15

Con 7 gruppi tutti i possibili confronti sono 21

Con 8 gruppi tutti i possibili confronti sono 28

 

Esempio 1.   In un esempio precedente, si è dimostrato che esiste una differenza significativa tra le mediane delle emissioni gassose giornaliere di 6 zone di una città, rilevate per 15 giorni.

Nella tabella sottostante, sono state riportate le medie dei ranghi:

 

 

 

Con confronti multipli a posteriori, si vuole verificare tra quali zone esista una differenza significativa, alla probabilità a_T = 0.05.

 

Risposta. Tra le medie dei ranghi delle 6 zone è possibile calcolare 15 differenze (). Per una visone complessiva, esse sono utilmente riportate (in valore assoluto) in una matrice triangolare

 

 

 

 

Per una probabilità complessiva prefissata  a_T = 0.05 in un test a due code, con 15 medie a confronto simultaneo la probabilità a per ogni media è 0.05/(15x2) uguale a 0.00167.

Alla probabilità a = 0.00167 nella distribuzione normale corrisponde un valore di Z uguale a 2,935 (approssimativamente la metà fra Z = 2,93 della probabilità P = 0.0017 e Z = 2,94 della probabilità P = 0.0016).

La tabella dei valori Z riportata in precedenza semplifica la modalità per ottenere questa stima,

- fornendo 2,935 per a_T = 0.05 e P = 15.

 

Applicando la formula

 con N = 15   e   k = 6,

 la differenza minima significativa D  tra le due medie dei ranghi

 

 è uguale a 2,01.

 

Confrontando il valore calcolato con le 15 differenze riportate nella tabella triangolare, risulta significativa solamente la differenza (uguale a 2,27) tra la media dei ranghi del gruppo D (uguale a 4,60) e quella del gruppo E (uguale a 2,33).

 

 

Quando entro i k gruppi esiste un trattamento usato come controllo, per cui i risultati degli altri k-1 trattamenti vengono confrontati solamente con il controllo, la significatività di ognuna delle k-1 differenze possono essere verificate con la stessa metodologia.

Di conseguenza, la probabilità a del confronto di ogni singolo trattamento con il controllo risulta più alta di quella stimata per i confronti precedenti:

-          il numero di confronti diventa k-1, per cui il valore di a_T complessivo deve essere diviso per k-1;

-          inoltre, poiché sono confronti unilaterali, non è richiesto di dimezzare ulteriormente la probabilità;

-          infine, occorre utilizzare la distribuzione Q di Dunnett, qui riportata, che tiene in considerazione anche gli effetti della non indipendenza dei vari confronti.

 

 

 

VALORI DEL Q DI DUNNETT

PER CONFRONTI MULTIPLI TRA P TRATTAMENTI E UN CONTROLLO

IN FUNZIONE DI a_T E DEL NUMERO N DI CONFRONTI

 

 

 

E’ possibile valutare la significatività della differenza tra il controllo ( C ) e un generico trattamento (T) utilizzando la differenza

-          tra le somme dei ranghi,

-          tra le medie dei ranghi.

 

 

Sono significative le differenze D tra le somme dei ranghi del gruppo Controllo (R_C) e di un generico gruppo Trattamento (R_T)

 quando

 

 

Sono significative le differenze D tra le medie dei ranghi del generico gruppo A () e del generico gruppo B ()

 quando

 

 

ESEMPIO 2. Riprendendo i dati dell’esempio precedente (N = 15)

 

 

 

 si assuma che sia noto da tempo che la zona P, periferica e residenziale, caratterizzata da un traffico significativamente minore, abbia i livelli d’inquinamento più bassi della città e sia stata assunta come modello per una politica ambientale.

Verificare quali altre zone hanno un livello significativamente maggiore di essa, alla probabilità complessiva a = 0.05 e alla probabilità a = 0.01.

 

Risposta. Le differenze tra la medie dei ranghi della zona di controllo P (con inquinamento minimo) e quelle delle altre 5 zone (A, B, C, D, E) sono  riportate nella tabella

 

 

 

Utilizzando la formula per le medie e ricavando dalla tabella che, in un test unilaterale di 4 confronti con  N = 15   e   k = 6,  poiché

-          per a = 0.05 il valore di Q è 2,16

-          per a = 0.01 il valore di Q è 2,77

 il valore D per a = 0.05

 è

 uguale a 1,48 (arrotondato in eccesso, come richiesto dal principio di cautela);

 il valore D per a = 0.01

 è

 uguale a 1,90 (arrotondato in eccesso, come richiesto dal principio di cautela).

 

In conclusione, alla probabilità complessiva

-          a_T = 0.05  rispetto all’inquinamento della zona di riferimento P (2,33) risulta maggiore quello rilevato nella zona A (3,86);

-          per a_T = 0.01 sono significativamente maggiori quello rilevato nella zona B (4,26) e quello della zona D (4,60).

 

Questi test che utilizzano i ranghi sollevano obiezioni non banali sulla loro validità. Come affermato nel 1966 da R. G. Miller jr. nel suo testo Simultaneous Statistical Inference (edito da McGraw-Hill, New York) e nel 1969 da K. R. Gabriel con l’articolo Simultaneous test procedures, some theory of multiple comparison (pubblicato Annals of the Mathematical Statistics Vol. 40, pp.224-250), le medie dei ranghi di due gruppi dipendono dai valori presenti in altri gruppi, esclusi dal confronto specifico.

A maggior ragione, l’obiezione è valida per il test di Kruskall-Wallis.