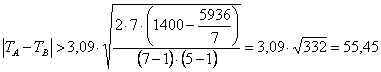TEST NON PARAMETRICI

PER PIU' CAMPIONI

 

 

15.12.  TEST DI QUADE

 

 

La proposta di Friedman del 1937 è la metodologia che si è affermata nell’uso dei ricercatori prima e nei programmi informatici dopo. Ora è riportata in quasi tutti i testi e i programmi di statistica, dai più semplici ai più diffusi. In letteratura esistono test equivalenti, proposti negli anni immediatamente successivi, quali:

-          Wallis W. A., 1939, The correlation ratio for ranked data, pubblicato su Journal of the American Statistical Association Vol. 34, pp. 533-538.

-          Kendall M. G., Babington Smith B., 1939, The problem of m-rankings, pubblicato da Annals of Mathematical Statistics Vol. 10, pp. 275-287.

-          Brown G. W. and Mood A. M., 1951, On Median Test for Linear Hypotheses, in Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, University of California Press, pp. 159-166.

Esistono anche proposte più recenti. Tra esse possono essere ricordate soprattutto quelle che analizzano l’interazione o permettono di valutare l’effetto dei blocchi:

-          Lehmann E. L., 1963, Asymptotically non parametric inference: an alternative approach to linear models, su Annals of Mathematical Statistics, Vol. 34, pp. 1494-1506.

-          Mehra K. L. Sen P. K., 1969, On a class of conditionally distribution-free tests for interaction in factorial experiments, su Annals of Mathematical Statistics, Vol. 40, pp. 658-664.

-          Mehra K. L. Smith G. E. J., 1970, On nonparametric estimation and testing for interactions in factorial experiments, su Journal of the American Statistical Association Vol. 65, pp. 1283-1296.

 

Tra questi sembra emergere il test di Dana Quade del 1979 (vedi l’articolo Using weighted rankings in the analysis of complete blocks with additive block effects su Journal of the American Statistical Association Vol. 74, pp. 680-683), utile nel caso di piccoli campioni e quando le righe hanno una variabilità molto differente. Sviluppa idee già presenti in un articolo di J. W. Tukey del 1957, oltre 20 anni prima “ Sums of Random Partitions of Ranks” (su Annals of Mathematical Statistics, Vol. 28, pp. 987-992).

Nell’articolo di Dana Quade sono presi in considerazione

-          le tabelle con una sola osservazione per trattamento x blocco,

-          la variabilità tra i blocchi, in aggiunta a quella entro i blocchi.

Soprattutto nel caso di pochi dati per trattamento, quindi con pochi blocchi e complessivamente pochi dati, appare intuitivamente ragionevole assumere che abbiano una credibilità maggiore i ranghi assegnati entro i blocchi con variabilità maggiore. Infatti, per semplice ragionamento deduttivo, i blocchi con variabilità piccola,

-          oltre ad avere con probabilità maggiore dei valori identici, che fanno perdere informazioni a tutto il sistema,

-          hanno valori tra loro molto vicini che, per il solo effetto del caso, ne possono modificare l’ordine con probabilità maggiore.

Nell’artico citato, l’autrice scrive :”Suppose the observations on different treatments are more distinct in some blocks than in the others; then it seems intuitively reasonable that the ordering of the treatments that these blocks suggest is more likely to reflect the underlying true ordering”.

 

La procedura

-          utilizza la distribuzione F di Fisher con df (k-1)  e  (k-1)×(N-1)

 e integra il metodo Friedman.

 Per una spiegazione semplice della procedura e un confronto dei risultati, è stato impiegato lo stesso esempio sulle quantità medie delle polveri Pm 10, in 5 zone di una città:

 

 

 

 dove   k = 5   e    N = 7.

Per verificare se esiste una differenza significativa tra le mediane dei valori riportati per le 5 zone, con ipotesi nulla

H₀:      contro     H₁: le me delle 5 zone non sono tutte uguali

 dai dati dapprima si derivano

-          sia la tabella dei ranghi entro i blocchi, con la metodologia di Friedman,

 

 

 

 

-          sia i ranghi dei blocchi (righe), in funzione delle dimensioni del loro campo di variazione, assegnando 1 a quello minore e N a quello maggiore:

 

 

 

 

- Successivamente, mediante

 dove

-            è il rango del campo di variazione della riga (nel confronto delle N righe),

-           è il rango di ogni valore entro riga (con k dati),

 si modifica la tabella dei ranghi e si calcola la somma per colonna, ottenendo

 

 

 

Ad esempio, in essa

-          il rango di A1 (4 in quella di Friedman) diventa  = 4

-          il rango di A2 (5 in quella di Friedman) diventa  = 8

-          il rango di E7 (1 in quella di Friedman) diventa  = -6

 

E’ possibile verificare di non aver commesso errori in questa trasformazione dei ranghi di Friedman, in quanto

-          la somma di ogni riga è uguale a zero

-          la somma dei totali di colonna è uguale a zero.

 

Infine da questa ultima tabella mediante

 

 dove

-          N = 7   e   k = 5

-           = (38)² + (46)² + (-26)² +(-26)² + (-32)² = 1444 + 2116 + 676 + 676 + 1024 = 5936

-           (dato dalla somma dei quadrati di tutti i ranghi modificati) = 1400 come nella tabella

 

 

 si ottiene

 

 

 un valore di W = 9,217 che deve essere confrontato con

- il valore critico di F per gdl (5-1) e (5-1)×(7-1), cioè 4 e 24.

Poiché il valore critico di F con df 4 e 24

-          alla probabilità a = 0.001 è uguale a 7,39

 si rifiuta l’ipotesi nulla di uguaglianza delle mediane dei valori giornalieri riportati, con probabilità di commettere un errore di primo tipo P < 0.001.

Con il test di Friedman si era trovato un valore di Fr = 22,27 ovviamente sempre con df 4 e 24. Con il test di Quade si è ottenuto un valore inferiore, perché le righe con la variabilità maggiore (la 3 e la 6), quindi quelle che logicamente meglio permettono di definire i ranghi entro esse, hanno una distribuzione dei ranghi differente dalle altre 5.

In condizioni sperimentali differenti, può fornire un risultato più significativo del test di Friedman: è una opportunità in più per il ricercatore che vorrebbe dimostrare l’esistenza di differenze significative tra le mediane dei gruppi.

 

Nel suo articolo, Quade propone anche

-          formule che utilizzano la distribuzione c² e

-          altre che utilizzano la distribuzione Z.

In un suo rapporto precedente del 1972, difficile da reperire nelle biblioteche e da lei citato, (Analizing Randomized Blocks by Weighted Rankings, Report SW 18/72 of the Mathematical Center, Amsterdam) Dana Quade ha anche fornito tabelle di valori critici per campioni di piccole dimensioni.

Tra i testi italiani, il test di Quade è riportato da Mario Castino e Ezio Roletto in Statistica Applicata. Metodi di trattamento dei dati per studenti universitari, ricercatori e tecnici (Piccin, Padova, 1991, pp. 494). In esso è illustrato anche un metodo per i confronti multipli a posteriori, che utilizza il principio del Bonferroni e la distribuzione t di Student (qui è modificata solo la simbologia, per mantenerla uguale a quella utilizzata nel test).

 

Per i confronti multipli del test di Friedman, Castino e Roletto riportano che la differenza tra le mediane del generico trattamento A e del generico trattamento B sono significativamente differenti,

 quando

 dove

-          T_A e T_B sono i totali dei ranghi delle colonne (trattamenti) A e B a confronto,

-          t è il  di Student alla probabilità a/2 con gdl n = (N-1)×(k-1).

 

Per i confronti multipli del test di Quade, riportano la stessa formula. Per i valori di r_ij e T_i devono essere utilizzati quelli calcolati nella tabella dei ranghi modificati secondo la metodologia di Quade.

Nella presentazione del metodo, anche in questo caso Castino e Roletto consigliano l’uso del t di Student senza tenere in considerazione i problemi di stima di a derivanti dal principio del Bonferroni, cioè senza valutare la relazione esistente tra comparison-wise e experiment-wise. Il loro metodo è quindi corretto solamente se a priori è stato programmato un solo confronto.

 

ESEMPIO. Poiché il risultato del test di Quade è stato significativo, confrontare tra loro le mediane delle 5 zone alla probabilità complessiva a_T = 0.05.

 

Risposta. La probabilità a di ogni confronto dipende dal numero di confronti che si vogliono effettuare. Se sono tutti quelli possibili a coppie tra le 5 mediane, essi sono 10; di conseguenza, per un probabilità  totale o experiment-wise pari a a_T = 0.05 il valore di comparison-wise è a = 0.005.

 

La differenza minima significativa (metodo favorito dal fatto di avere necessariamente campioni con lo stesso numero di osservazioni) con

-          N = 7   e   k = 5

-            = 5936     e       = 1400

-          gdl = 24 e quindi t = 3,09 in una distribuzione bilaterale

 è

 

 uguale a 55,45

Dalla tabella delle somme dei ranghi di Quade effettuate per colonna (T_i)

 

 

 

 si ricava la matrice delle differenze in valore assoluto

 

 

 

Alla probabilità complessiva a_T = 0.05 sono significative tutte le differenze maggiori di 55,45 (segnate con asterisco).

Tale conclusioni devono essere trasferite alle mediane dei dati originali raccolti.