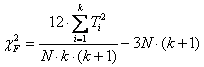TEST NON PARAMETRICI

PER PIU' CAMPIONI

 

   

15.13. L’ESEMPIO DI KOCH: USO DI METODI NON PARAMETRICI, NELL’ANALISI STATISTISTICA DI UN ESPERIMENTO COMPLESSO CON K FATTORI

 

 

Tutti i test non parametrici presentati in questo capitolo e in quelli precedenti sono stati applicati a casi semplici. Anche nella verifica dell’uguaglianza tra k mediane o varianze, le analisi più sofisticate, è sempre stato preso in considerazione un solo fattore.

Per esperimenti più complessi, quali l’ANOVA a due o a più criteri con interazione, è prassi ricorrere alle tecniche parametriche. Tuttavia, è possibile giungere a soluzioni anche mediante l’uso congiunto di alcuni metodi parametrici già presentati, con il vantaggio rilevante di evitare le obiezioni collegate al tipo di scala e alla distribuzione dei dati.

Già nel 1970, Gary G. Koch nel riassunto del suo articolo The use of non-parametric methods in the statistical analysis of a complex split plot experiment (pubblicato su Biometrics Vol. 26, n. 1-4 pp. 105-128) scriveva: “Da tempo gli statistici devono confrontarsi con dati che provengono da dati sperimentali complessi e che non soddisfano alle ipotesi tradizionali di validità dell’analisi della varianza, vale a dire alle ipotesi di indipendenza, d’omogeneità delle varianze e di normalità. Qualche volta lo statistico risolve queste situazioni aggiustando i dati con trasformazioni di variabili o arrivando a scartare certe osservazioni estreme. Benché queste procedure possano condurre spesso a analisi soddisfacenti, i risultati così ottenuti possono essere messi in discussione.

L’oggetto di questo articolo è di mostrare che i metodi non parametrici sono in grado di fornire alternative realiste nell’analisi di questi dati. Le procedure presentate sono fondate sui ranghi. Benché siano valide in condizioni molto generali, esse hanno buone proprietà di potenza”.

 

E’ uno degli esempi didatticamente più completi, che ricorre all’uso congiunto di vari test e che può essere utilizzato come traccia per analisi simili in molti settori della statistica applicata. Questo articolo è riportato, con modifiche, da Giampiero Landenna e Donata Marasini nel loro volume del 1990 Metodi statistici non parametrici (Il Mulino, Bologna, pp. 511, a pp. 278-283). E’ il testo italiano di statistica non parametrica più completo, valido anche in un confronto internazionale: ricchissimo di bibliografia, utilizza un linguaggio statisticamente sempre rigoroso, ma non semplice da comprendere, per “utenti” della statistica che non abbiano già acquisito conoscenze di buon livello.

 

L’esperimento considera tre fattori e le loro interazioni: la quantità di ferro assorbita dal fegato di topo albini, considerando

-          l’effetto della temperatura (a due livelli),

-          l’effetto della dieta (a due livelli),

-          gli effetti del livello di acidità della soluzione (a tre livelli),

-          con le loro interazioni di primo e di secondo livello.

 

 

 

A questo scopo, sono stati presi 34 topi albini di sesso maschile, ognuno con un peso di circa 200 grammi.

Con questi 34 soggetti, sono stati costruiti due campioni dipendenti, formando 17 coppie. Un individuo per ogni coppia, scelto casualmente, ha avuto una dieta contenente etionina, l’altro una dieta di controllo.

Dopo 7 giorni, a questi 34 animali è stato estratto il fegato. Ogni fegato è stato suddiviso in tre parti e, per scelta casuale, posti in tre differenti soluzioni di ferro radioattivo con acidità bassa (pH 7,0 - 7,7), media (pH 4,5 – 5,5), alta (pH 2,0 – 3,0).

Infine sono stati fatti 2 blocchi: il primo, formato dalle tre parti del fegato di 8 coppie, scelte a caso, è stato posto in ambiente a 37° centigradi; il secondo blocco, formato dalle tre parti del fegato delle altre 9 coppie, è stato posto a 25° centigradi.

Conclusi i trattamenti, l’analisi chimica della quantità di ferro radioattivo assorbito dai 102 campioni ha dato i risultati riportati nella tabella precedente.

 

Nell’analisi statistica, che verrà descritta in modo dettagliato, l’autore dell’articolo considera gli individui delle 17 coppie come due campioni dipendenti. In realtà non lo sono, poiché non è stato seguito alcun criterio oggettivo. Infatti l’articolo riporta che esse sono state formate per scelta puramente casuale: “The design was as follows: 34 male albino rats, each weighing approximately 200 grams, were randomly divided into 17 pairs”.

Landenna e Marasini si accorgono di questo errore concettuale e rimediano aggiungendo, nella loro presentazione dell’esperimento, che le coppie sono state costruite in modo tale che la differenza di peso fra i due ratti fosse la minima possibile.

 

E’ un esperimento a struttura gerarchica, in cui

-          le coppia sono nested nella temperatura,

-          gli animali sono nested nelle coppie,

-          le tre parti dello stesso fegato sono nested negli animali.

 

E’ sufficiente la semplice lettura dei dati riportati nella tabella per rilevare la presenza di un numero non trascurabile di valori particolarmente alti, che allontanano la distribuzione dalla normalità facendole assumere forma bimodale. La loro eliminazione determina la perdita di informazioni, circa gli effetti dei fattori su alcuni animali.

L’assunzione di omogeneità della varianza non è corretta. Infatti le varianze () dei due blocchi, distinte per soluzione, sono

 

 

 

Con il test più semplice e tra i meno potenti (il test di Hartley), il rapporto tra la varianza maggiore (10,89) e quella minore (0,15)

  è uguale a 72,6. Nella tabella dei valori critici di Hartley, il valore critico per k = 12 e df = 8 è

-          12,7 alla probabilità a = 0.05

-          21 alla probabilità a = 0.01.

Il test dimostra la non omogeneità delle varianze, con probabilità P nettamente inferiore a 0.01.

Sempre nell’articolo citato, Koch afferma che benché la eterogeneità della varianza possa essere eliminata con una trasformazione, certe inconsistenze potrebbero rimanere. Inoltre, nell’analisi dei risultati, molti ricercatori preferiscono utilizzare i dati non trasformati perché assumono significati più evidenti e semplici per l’interpretazione dei risultati.

 

Un altro aspetto che evidenza come manchino le condizioni di validità per applicare un test parametrico è la relazione significativa tra le serie dei valori entro i due blocchi, in particolare nelle combinazioni temperatura x dieta.

 

 

 

 

La lettura delle due tabelle di correlazione parametrica evidenzia:

-          le risposte delle differenti frazioni di fegato entro lo stesso animale tendono a non essere ugualmente correlate;

-          le risposte degli animali entro la stessa coppia e associate allo stesso livello di acidità tendono ad essere più altamente correlate delle risposte con livelli di acidità differenti.

Per una interpretazione più completa, è utile ricordare che nella tabella per la significatività dei coefficienti di correlazione parametrica (vedi capitolo relativo) è riportato che

-          con df = 6 (come per il Blocco 37° C) il valore critico alla probabilità a = 0.05 è 0,7067 mentre alla probabilità  a = 0.01 è 0,8343

-          con df = 7 (Blocco 25° C) il valore critico alla probabilità a = 0.05 è 0,6664 mentre alla probabilità a = 0.01 è 0,7977.

Nelle due tabelle precedenti, i valori di correlazione segnati con asterisco superano la soglia critica del 5%.

 

Nei capitoli dedicati all’ANOVA, è già stato illustrato come l’analisi statistica parametrica permetta di evidenziare l’effetto dei singoli fattori e delle loro interazioni, in accordo con il modello

 dove

-          m è la media generale,

-          a_i è l’effetto della temperatura,

-          b_j è l’effetto della dieta,

-          g_k è l’effetto del livello di acidità della soluzione,

-          ab_ij, ag_ik, bg_jk sono le rispettive interazione di primo livello,

-          abg_ijk è l’interazione di secondo livello.

 

I risultati dell’ANOVA pubblicati nell’articolo di Koch sono i seguenti:

 

 

 

Trattandosi di un esperimento nested complesso, i diversi valori di F riportati nella tabella sono stati ottenuti da rapporti differenti, qui indicati nei punti fondamentali:

 

-          il valore di F per la significatività delle differenze tra le medie delle due temperature è dato da

  e non è significativo in quanto addirittura inferiore a 1;

 

-          il valore di F per la significatività delle differenze tra le medie delle due diete è dato da

 e risulta  altamente significativo in quanto maggiore del valore critico, che per F_(1,15) e a = 0.001 è 19,5;

 

-          il valore di F per la significatività delle differenze tra le medie dei tre livelli di acidità

 è altamente significativo, in quanto maggiore del valore critico di F_(2,30) e a = 0.001 che  è 9,9.

Le varie interazioni (riportate nella tabella ANOVA) non risultano significative.

Con test di statistica non parametrica è possibile condurre le stesse verifiche, seppure separatamente per ogni fattore; ma alla fine si perviene ugualmente a una visione complessiva come la precedente

 

A) Per valutare l’effetto della temperatura, si aggregano i dati relativi ad ogni coppia di ratti come

 

 

 

 

Per verificare l’ipotesi nulla bilaterale

H₀:        contro      H₁: 

 si ricorre al test U di Mann-Whitney per due campioni indipendenti. L’ipotesi è bilaterale, in quanto all’autore non è apparso logico non assumere a priori il vantaggio di una delle due condizioni sperimentali (temperatura a 35° C oppure a  25° C), nell’assorbimento della quantità di ferro (ricordare che l’ipotesi dipende solo dalla conoscenza a priori dell’effetto della temperatura).

 

In modo più dettagliato, in funzione della temperatura (colonna 1), si raggruppano i dati di tutte le coppie (colonna 2), separatamente per il Controllo (colonna 3) e il Farmaco (colonna 4), calcolandone la somma (colonna 5).

Il gruppo delle 8 coppie collocate a 37° C e quello delle  9 coppie a 25° C formano due campioni indipendenti.

 

Pure volendo utilizzare il test U di Mann-Whitney, in quanto più diffuso anche nei programmi informatici, la organizzazione dei dati nella tabella rende più semplice utilizzare il conteggio dei ranghi, secondo il metodo T di Wilcoxon-Mann-Whitney.

Si ottiene

T(37°) = 8 + 2 + 17 + 9 + 4 + 6 + 10 + 15 = 71

T(25°) = 14 + 12 + 7 + 1 + 13 + 16 + 5 + 3 + 11 = 82

 

Successivamente, sulla base della relazione

 si ricavano i corrispondenti valori di U e U’

 

 

 

La relazione

 permette di verificare con facilità di non avere commesso errori nel calcolo dei ranghi e nella loro trasformazione in precedenze.

Poiché il valore critico (vedi tabella relativa al test U di Mann-Whitney nel capitolo dedicato ai test non parametrici per 2 campioni indipendenti) alla probabilità a = 0.05 per un test bilaterale è 13 (molto minore del valore 35 calcolato), non si può rifiutare l’ipotesi nulla: le due differenti temperature non producono differenze nella quantità media di ferro assorbito.

Inoltre è utile osservare che il valore di U calcolato (35) non solo è maggiore di quello critico, ma è molto vicino alla media attesa (36)

m_U =

E’ quindi possibile concludere non solo che non è possibile rifiutare l’ipotesi nulla, ma che con altissima probabilità essa è vera.

 

 

B) Per valutare l’effetto della dieta (a_i) contenente etionina rispetto al controllo, sempre partendo dalla tabella dei dati presentati, si formano due campioni dipendenti, in cui la quantità per ogni ratto è dato dalla somma delle quantità misurate nelle tre soluzioni:

 

 

 

Considerando le coppie di ratti, si confrontano le due mediane (quella del Farmaco e quella del Controllo) con ipotesi unilaterale

H₀:       contro      H₁:

 attraverso il test T di Wilcoxon per due campioni dipendenti.

 

In questo caso, è stata scelta un’ipotesi unilaterale,  in quanto ritenuto logico che il farmaco possa determinare un aumento reale della quantità di ferro assorbita dal fegato.

 

La descrizione dettagliata della procedura riportata nella tabella prevede: per ogni coppia (colonna 1), si sommano le quantità del Controllo (colonna 2) e del Farmaco (colonna 3), calcolandone l’incremento con il segno (colonna 4); con questi ultimi dati presi in valore assoluto, si stima il rango (colonna 5) e a ognuno si attribuisce il segno dell’incremento (colonna 6).

La somma minore dei valori con lo stesso segno (il negativo) risulta T = 2.

Poiché il valore critico (vedi tabella relativa al test T di Wilcoxon nel capitolo dedicato ai test non parametrici per 2 campioni dipendenti) alla probabilità a = 0.0005 per un test unilaterale è 11, si rifiuta l’ipotesi nulla: il farmaco determina un aumento altamente significativo della quantità mediana di ferro.

 

 

C) Per valutare l’effetto della acidità, si aggregano i dati relativi ad ogni coppia di ratti come nella tabella seguente:

 

 

 

Per verificare l’ipotesi nulla sulle mediane dei tre livelli di acidità con

H₀:        contro      H₁: le me non sono tutte uguali

 si ricorre al test di Friedman per campioni dipendenti.

Per semplificare i calcoli, si può utilizzare la formula abbreviata che ricorre ai totali dei ranghi

 

 

 dove:

-          N  è il numero di righe od osservazioni in ogni campione  (17),

-          k  è il numero di colonne o campioni a confronto (3),

-           è il totale dei ranghi di ogni colonna (24,  36,  42)

 ottenendo

 

 un valore uguale 9,88 da verificare nella distribuzione chi-quadrato con 2 gdl.

Poiché la tabella dei valori critici

-          alla probabilità a = 0.01 riporta 9,21

-          alla probabilità a = 0.001 riporta 13,82

 si rifiuta l’ipotesi nulla con probabilità P < 0.01.

I tre livelli di acidità determino una differenza significativa nelle quantità mediane di ferro assorbito.

Per verificare se la quantità aumenta in modo significativo al crescere del livello di acidità, si dovrebbe applicare il test di Page, che è presentato nel capitolo successivo. Si tratta di un test unilaterale; applicato agli stessi dati, darebbe una probabilità dimezzata rispetto a quella ora calcolata, se effettivamente esiste un gradiente in crescita della quantità mediana di ferro assorbito nei tre livelli crescenti di acidità. (Ma Koch ha applicato il test di Friedman, forse perché test non parametrico analogo all’ANOVA a due criteri).

 

 

Nello stesso modo con il quale sono stati analizzati gli effetti dei tre fattori principali e possibile analizzare le loro interazioni. Si tratta di riorganizzare ogni volta la tabella dei dati originali in modo adeguato, applicando il metodo richiesto

-          dall’ipotesi da verificare e

-          dalla impostazione tabellare dei dati.

 

 

D) Per verificare se esiste interazione Temperatura x Dieta, i dati devono essere separati nei 4 gruppi:

-          temperatura 37° C  e farmaco (8 dati),

-          temperatura 37° C  e controllo (8 dati),

-          temperatura 25° C  e farmaco (9 dati),

-          temperatura 25° C  e controllo (9 dati),

 

 

 

 

Separatamente per temperatura (colonna 1), per le 17 coppie (colonna 2) formate dal totale del Farmaco (colonna 3) e dal totale del Controllo (colonna 4) si determinano le differenze (colonna 5) e si attribuiscono ad esse i ranghi considerando tutta la colonna (colonna 6).

Infatti, il concetto di base è che, se non esiste interazione fra Temperatura e Dieta, la mediana delle differenze tra i totali delle coppie con temperatura di 37° C non differisce significativamente dalla mediana delle differenze  tra i totali delle coppie con temperatura 25°C.

Diventa il confronto tra le mediane di due campioni indipendenti, che può essere verificata con il test U di Mann-Whitney. Anche in questo caso, a causa della disposizione tabellare dei dati, risulta più semplice utilizzare la somma dei ranghi per ricorrere al test T di Wilcoxon-Mann-Whitney o, mediante trasformazione, ricavare il valore di U.

 

T(37°) = 8 + 5 + 14 + 13 + 3 + 9 + 7 + 10 = 69

T(25°) = 12 + 16 + 11 + 1 + 6 + 15 + 2 + 4 + 17 = 84

 

Successivamente, sulla base della relazione utilizzata anche in precedenza si ricavano i corrispondenti valori di U e U’ (preferito nei programmi informatici e nelle indicazioni di molti testi)

 

 

 

La relazione

 permette di verificare con facilità di non avere commesso errori nel calcolo dei ranghi e nella loro trasformazione in precedenze.

Poiché il valore critico (vedi tabella relativa al test U di Mann-Whitney nel capitolo dedicato ai test non parametrici per 2 campioni indipendenti) alla probabilità a = 0.05 per un test bilaterale è 13 (molto minore del valore 33 calcolato), non è possibile rifiutare l’ipotesi nulla: non esiste una interazione significativa tra Temperatura e Dieta.

Ancora una volta si può osservare, che il valore di U calcolato (39) non solo è maggiore di quello critico, ma è molto vicino alla media attesa (36)

m_U =

E’ quindi possibile concludere non solo che non è possibile rifiutare l’ipotesi nulla, ma che probabilmente essa è vera: l’interazione tra Temperatura e Dieta è nulla.

 

 

E) Per verificare la significatività delle interazioni nelle quali si prende in considerazione l’Acidità, l’analisi diventa più complessa, poiché essa è a tre livelli. Di conseguenza, il modello di analisi applicato in precedenza alla dieta deve considerare le differenze tra tutte le possibili coppie di acidità, che per tre livelli sono tre: Bassa – Media, Bassa – Alta, Media – Alta.

Ne deriva una matrice di ranghi delle 17 coppie di ratti, distinti nei due livelli di temperatura, con i tre ranghi delle differenze tra le coppie dei livelli di acidità.

 

E’ un’analisi con ricorre con poca frequenza e che pertanto non viene illustrata. È riportata solamente la tabella dei dati che dovrebbero essere analizzati:

 

 

L’articolo di Gary G. Koch chiarisce che anche le tecniche non parametriche dimostrano la non significatività sia di tutte le interazioni di primo livello, sia di quella di secondo livello.

Nelle conclusioni presenta una tabella riassuntiva di tutte le analisi (leggermente modificata).

Per rendere i confronti omogenei e di facile lettura, i risultati di tutti i test non parametrici effettuati sono stati trasformati nei valori c² corrispondenti,

 

 

Il confronto con i valori critici mostra che si è giunti globalmente alle stesse conclusioni permesse dall’ANOVA parametrica a due fattori con interazione.

Questi test non parametrici non solamente sono applicabili in condizioni molto più generali, ma hanno esattamente la stessa potenza nell’evidenziare effetti significativi.

 

 

L’articolo di Koch evidenzia anche un ultimo aspetto, che sottolinea concetti già presentati in questo corso, nel paragrafo introduttivo ai test non parametrici. Per la sua importanza viene riportata in modo integrale (modificando solo la grafica, per mettere in risalto alcuni concetti):

 Finally, some remarks should be made about a paradoxical aspect of the analysis given here. Namely, we claim that because its underlying assumptions do not hold, the analysis of variance is not appropriate. However, it is performed anyway and then is used as a standard to which the results of the non-parametric tests are compared. This has been done for two reasons:

1.       The analysis of variance plays a sacred role in statistical analysis because of its robustness properties.

2.       For this set of data, the results of the parametric and non-parametric analysis are similar.

 

To avoid the confusions created, we recommend that three cases be delineated as follows:

   I .   The assumptions of the analysis of variance definitely hold.

   II.  The assumptions of the analysis of variance are not drastically violated.

   III. The assumptions of the analysis of variance are drastically violated

 

If Case I applies, only the analysis of variance need be performed.

If Case III applies, only the non-parametric analysis should be performed.

If Case II applies, both the analysis of variance and the non-parametric analysis should be performed, and hopefully they will lead to the same conclusions.

 

The data considered in this paper represent a Case II situation.