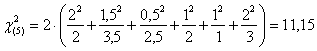TEST NON PARAMETRICI

PER PIU' CAMPIONI

 

 

15.2.   ESTENSIONE DEL TEST DELLA MEDIANA

 

 

L'estensione a k campioni (con k > 2) del test della mediana (the median test for several samples) serve per verificare l’ipotesi se le tendenze centrali sono significativamente differenti. Anche questo è concettualmente molto semplice e non ha un autore definito, in quanto diffuso fin dalle prime proposte sul chi quadrato.

 

L’ipotesi nulla, che prende in considerazione le mediane (me) delle popolazioni dalle quali sono state estratti i vari campioni (A, B, …, K), è che esse siano tutte uguali

H₀: me_A = me_B = … = me_K

 mentre l’ipotesi alternativa, solo bilaterale come in tutti i confronti multipli effettuati simultaneamente, è

H₁: le mediane dei k gruppi non sono tutte uguali

 

E’ fondato sulle tecniche di analisi di una tabella k x 2 con il c² o il test G quando il numero di osservazioni è sufficientemente grande; ricorre alla distribuzione ipergeometrica quando il numero di osservazioni è limitato o quando, come ora, è possibile disporre di un computer che svolga la rilevante quantità di calcoli richiesta in un campione grande. 

Rispetto ai vari test sulla tendenza centrale, è utilizzato in modo appropriato quando le misure sono approssimate e possono essere ordinate per rango solo in modo parziale, con molti valori identici, in particolare se collocati agli estremi.. In altri termini, quando la distribuzione è lontana dalla normalità e presenta molti ties.

 

Nella raccolta dei dati ambientali, biologici e medici, può succedere di utilizzare strumenti tarati con alta precisione per i valori centrali, più frequenti; ma che non siano in grado di valutare le misure collocate verso gli estremi, più rare, troppo piccole per essere rilevate o troppo grandi per essere determinate con la stessa precisione di quelle intorno alla norma.

Si deve ricorrere necessariamente al test della mediana anche nell'analisi di distribuzioni in cui le misure estreme siano state raggruppate in classi aperte, formate da valori minori (< X) e/o maggiori (> X) di una quantità determinata.

 

Per i calcoli manuali, il fattore limitante all’uso del test della mediana per k campioni indipendenti è quello del c² o del test G; il numero di osservazioni deve essere sufficientemente elevato.

Nel caso di k campioni con un numero di osservazioni molto ridotto, si può utilizzare il metodo esatto, fondato sulla distribuzione ipergeometrica, analogo al metodo esatto di Fisher in tabelle 2x2; ma richiede molti calcoli e quindi è praticamente applicabile solo con programmi informatici.

 

Il metodo dell'estensione del test della mediana per il confronto tra le tendenze centrali di più campioni può essere schematizzato in alcuni punti fondamentali, seguendo la sua applicazione ad un esempio.

 

1 – Dopo aver raccolto i dati di k campioni indipendenti, con un numero r di osservazioni che può essere diverso, come nell’analisi della varianza ad un criterio di classificazione,

 

 

 

2 - ordinare per ranghi tutte le osservazioni dei k gruppi a confronto, come se fossero un gruppo unico, mantenendo per ogni valore l'informazione del gruppo di appartenenza

 

 

 

3- Identificare la mediana di questa distribuzione unica,

 che con  dati dell’esempio è l’8° valore, il 2,5 del gruppo B (in grassetto).

Poiché il dato successivo ha un valore identico, collocare la mediana tra il 7° e l’8° valore.

 

4 - Contare quante sono le osservazioni di ogni gruppo che hanno valore inferiore (n₁) e quante quelle che hanno valore superiore (od uguale, in questo caso) (n₂) alla mediana:

 

 

 

L'eventuale valore corrispondente alla mediana può essere classificato in uno dei due sottogruppi indifferentemente (in questo caso è stato contato con quelli superiori alla mediana).

Con k gruppi si ottiene una distribuzione di frequenza in una tabella k x 2, come quella appena  riportata.

 

 

5 - Se è vera l'ipotesi nulla (H₀: i vari gruppi a confronto sono estratti dalla stessa popolazione o da campioni con la stessa tendenza centrale), ogni gruppo dovrebbe avere lo stesso numero di osservazioni prima e dopo la mediana; se i due gruppi non hanno la stessa frequenza, la stima delle frequenze attese può essere fatta come nella tabella riportata

 

 

 

 

Se l’ipotesi nulla è falsa, almeno un gruppo dovrebbe avere una prevalenza significativa di osservazioni con valore minore o maggiore della mediana.

 

 

6 - Nel caso di campioni grandi, l’accordo tra la distribuzione osservata e la distribuzione attesa può essere analizzata con il test  corrispondente (o il test G), con gdl uguali a k – 1 (k = numero di gruppi).

 

 

7- Se i campioni sono piccoli si ricorre al metodo esatto, disponendo di un programma informatico adeguato.

Indicando con

 

 

 

 

dove

-          a, b, c, d, e, f,  sono le frequenze inferiori e superiori alla mediana nei k gruppi,

-          n₁, n₂ , n₃ , n₄ , n₅ , N   sono rispettivamente i totali marginali e il totale generale

 la formula generale per calcolare la probabilità esatta della risposta specifica ottenuta, derivata dalla distribuzione ipergeometrica è

Pe =

 nel caso di tre gruppi;

 è facilmente estensibile a k gruppi mediante

 

Pe =

 

Con questa formula, si stima la probabilità di avere solo la risposta sperimentale.

Come nel metodo esatto di Fisher, la probabilità calcolata deve essere sommata con quelle di tutte le risposte più estreme. Poiché in questo caso si tratta di un test bilaterale (come sempre con k campioni), le risposte più estreme possono essere individuate con facilità dal valore della loro probabilità esatta: sono risposte più estreme tutte quelle che hanno una probabilità inferiore a quella calcolata per la risposta sperimentale.

 

 

ESEMPIO 1.   Si intende verificare se esiste una differenza significativa nella densità (numero di individui entro una superficie unitaria) di 5 specie vegetali (A, B, C, D, E). A questo scopo è stato raccolto un numero variabile di campioni, in aree di dimensione diversa, stimandone la concentrazione media in modo approssimato.

 

 

 

 

Le 5 aree hanno una concentrazione mediana significativamente differente?

 

Risposta.

1 - I rapporti sono stati calcolati su k (con k > 2) campioni di superficie non costanti e sono espressi con misure approssimate, che forniscono solo la dimensione del fenomeno, non una misura di una scala ad intervalli o di rapporti; di conseguenza, il test appropriato è l’estensione della mediana per k campioni.

 

L’ipotesi nulla è che tutti i campioni abbiano la stessa mediana

H₀: me_A = me_B = me_C = me_D = me_E

con ipotesi alternativa che almeno una sia differente o

H₁: non tutte le mediane sono uguali

 

2 - Come prima elaborazione dei dati, è utile costruire una distribuzione ordinata di tutti i valori, conservando per ognuno l'informazione del gruppo di appartenenza, allo scopo di

- determinare la mediana comune,

- contare per ognuno dei 5 gruppi a confronto quanti sono i valori inferiori e quelli superiori

 

<1	<1	<1	1	1	2	2	2	2	3	3	3	3	4	4	4	4	5	5	5	5
A	A	C	A	A	A	B	C	C	A	A	C	C	A	C	C	E	C	E	E	E
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	Segue

 

 

 

Nell'esempio, i dati sono 35: la mediana è il 18° valore e quindi 5. Poiché i valori identici alla mediana sono più di uno ed appartengono a vari gruppi, risulta utile aggregare il valore della mediana al gruppo dei valori maggiori di essa (>).

 

3 - Per ognuno dei 5 gruppi a confronto, si contano quanti sono i valori minori e quanti sono uguali o maggiori alla mediana. Si ottiene la tabella (5 x 2) seguente.

 

 

 

4 - Se è vera l'ipotesi nulla che tutti i gruppi hanno la stessa tendenza centrale, la distribuzione attesa è facilmente intuibile: ogni gruppo dovrebbe avere metà (nell'esempio esattamente 17/35) dei suoi valori prima della mediana e l'altra metà (esattamente 18/35) dei suoi valori dopo la mediana.

La significatività delle differente distribuzione dei 5 gruppi è verificata con un test  con 4 df.

Con i dati dell’esempio, il numero di dati potrebbe essere ritenuto insufficiente per una sua applicazione valida per il test c² o il test G, poiché tutte le 10 caselle delle frequenze attese hanno valori inferiori a 5. Sarebbe quindi più corretto l’uso della distribuzione ipergeometrica.

E’ una ulteriore conferma del fatto che, quando si utilizza in modo ridotto la quantità d’informazione contenuta nei dati raccolti, per raggiungere con il test la potenza sufficiente è necessario disporre di campioni di dimensioni relativamente grandi.

Nel caso del test chi quadrato, quando si hanno gruppi con un numero di osservazioni particolarmente ridotto è utile procedere ad una aggregazione delle classi; con i dati dell’esempio, sarebbe conveniente unire i 4 gruppi minori B e C, D e E in due soli gruppi secondo le loro affinità. Si ricostruiscono le condizioni di validità, che nella distribuzione attesa richiedono almeno 5 osservazioni per casella, anche se tale operazione comporta un’ulteriore perdita di informazione e non permette l’analisi dettagliata per ogni singola specie.

 

I programmi di computer di norma forniscono  almeno tre risultati, tra loro non identici:

- il valore del c² con gdl 4, (sovente, un secondo c² con la correzione di Yates),

- il valore del test G sempre con 4 gdl, (sovente, una seconda versione con la correzione di Williams o di Mantel-Haenzel),

- la probabilità esatta, stimata con la distribuzione ipergeometrica.

 

ESEMPIO 2. Tra i testi internazionali, il test della mediana per k campioni indipendenti è riportato nel volume di P. Sprent del 1993 (Applied Nonparametric Statistical Methods, 2^nd ed., Chapman & Hall, London), dal quale sono tratti l’esempio successivo e i commenti.

Sono stati raccolti 6 campioni di dati, contenenti rispettivamente  4,  7,  5,  4,  2,  6, osservazioni.

Il confronto con la mediana comune a tutti i dati ha fornito il seguente risultato

 

 

 

Verificare alla probabilità a = 0.05  l’ipotesi nulla

H₀: i sei campioni sono tutti estratti da popolazioni con la stessa mediana

 contro l’ipotesi alternativa bilaterale

H₁: le sei mediane non sono tutte uguali

 

Risposta. E’ possibile utilizzare il metodo classico

 

 

 per il quale è necessario stimare la distribuzione attesa, nella condizione che H₀ sia vera.

Poiché ogni gruppo dovrebbe avere metà delle osservazioni prima e metà dopo la mediana, la distribuzione attesa è

 

 

 

Il valore del chi quadrato risulta

 

 

 uguale a 11,15 con 5 df, mentre il valore critico alla probabilità a = 0.05 è 11,07.

Si rifiuta l’ipotesi nulla, con probabilità P < 0.05.

 

Secondo vari autori, i sei campioni dell’esempio sono piccoli e quindi sarebbe corretto utilizzare la distribuzione ipergeometica, invece di quella chi quadrato. Sprent osserva che

-          la probabilità calcolata con il  è esattamente P = 0.048,

-          mentre con un test esatto risulta P = 0.046.

Un risultato molto vicino., tale da confutare eventuali obiezioni di validità nonostante il non rispetto delle condizioni di validità, in totale (N < 30) per casella nella distribuzione attesa (n_i <5).