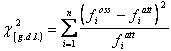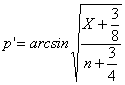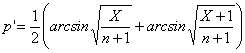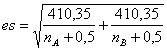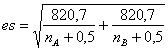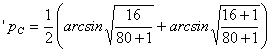TEST NON PARAMETRICI

PER PIU' CAMPIONI

 

 

15.7.  CONFRONTI TRA PIU' PROPORZIONI E CONFRONTI MULTIPLI RELATIVI.

 

 

Il confronto simultaneo tra più proporzioni è già stato illustrato nel capitolo III, presentando i metodi dei test c² e G in  tabelle di contingenza 2 x N.

E' già stato spiegato come in esperimenti che danno risposte binarie, ad esempio in un esperimento di ecotossicologia nel quale si confrontano gli effetti letali di 4 sostanze tossiche (A, B, C, D), per facilitare i calcoli successivi e meglio comprendere i risultati del test, i dati devono essere riportati in una tabella come la seguente

 

 

 

Successivamente si stimano le frequenze attese, nella condizione che l'ipotesi nulla sia vera.

Per ogni casella, la frequenza attesa è stimata facilmente con

Freq. attesa = Totale di riga  x  Totale di colonna  / Totale generale

 ottenendo

 

 

 

Infine si possono calcolare

-          il valore del c²  con 3 gdl mediante

 

 

-          il valore del G  con gli stessi gdl mediante

 

G_(gdl) =

 oppure mediante

 

 

Con gli stessi dati, per verificare l'ipotesi nulla

H₀: p_A = p_B = p_C = p_D

 contro l'ipotesi alternativa

H₁: non tutte le p sono uguali

 oppure

H₁: almeno due p sono tra loro diverse

 quando il campione è grande e le proporzioni non sono prossime a 1 oppure a 0 è possibile utilizzare il c² con una modalità che offre altre opportunità di analisi.

 

A questo scopo, è vantaggioso presentare gli stessi in una tabella differente, che meglio evidenzia

 

 

 

 

-          le varie proporzioni (p_i) di deceduti (o di sopravvissuti) a confronto,

-          le dimensioni di ogni campione,

-          la proporzione media complessiva () delle k classi.

 

Per verificare se le 4 proporzioni sono tra loro simili, si può ricorrere alla formula

 

 dove

-          X_i è la frequenza osservata per ogni classe o campione,

-           è il numero di dati rilevati per ogni classe  o dimensione di ogni campione,

-           può essere la media generale (nel caso dell'esempio è 0,317) ponderata oppure una proporzione  attesa qualsiasi con la quale si vuole effettuare il confronto. Si ricorre alla media generale se essa rappresenta la stima migliore dell'effetto dei k gruppi, supposti tutti uguali; si utilizza una frequenza attesa per verificare se essa globalmente può essere il vero effetto medio dei k gruppi.

 

Per comprendere la formula precedente, è utile

-          osservare come essa sia il quadrato di quella utilizzata per la distribuzione normale

 

 estesa a k proporzioni,

-          ricordare che .

 

 

ESEMPIO 1. Verificare se le proporzioni (p_i) dei decessi nei 4 esperimenti sono uguali, utilizzando i dati dell'ultima tabella.

 

Risposta. Per verificare l'ipotesi nulla

H₀: p_A = p_B = p_C = p_D

 si calcola il valore del c² con 3 gdl mediante

 

 ottenendo

 

 

  c²  = 6,79 con 3 gdl.

Poiché i valori critici con 3 gdl sono

-          7,815 per a = 0.05

-           6,231 per a = 0.01

 al valore calcolato corrisponde una probabilità P compresa tra 0.10  e  0.05.

In conclusione, con i dati raccolti non si può rifiutare l'ipotesi nulla, anche se è possibile affermare che l'esperimento è tendenzialmente significativo. Probabilmente, campioni con un numero maggiore di osservazioni avrebbero permesso di rifiutare l'ipotesi nulla.

 

Se l'informazione sui risultati è limitata alla sola conoscenza delle proporzioni (p_i), senza le dimensioni di ogni campione (n_i) o l'equivalente frequenza assoluta di casi postivi (X_i), quando si disponga di misure ripetute per ogni sostanza a confronto, è possibile utilizzare

-          l'ANOVA dopo trasformazione angolare per omogeneizzare le varianze, se le proporzioni sono calcolate su campioni di dimensioni simili,

-          l'analisi della varianza non parametrica (test di Kruskal-Wallis) come test più robusto, soprattutto se le dimensioni (n_i) di ogni campione sono diverse.

In entrambi i casi, dopo il rifiuto dell'ipotesi nulla, è possibile ricorrere ai confronti multipli, come già illustrato nei paragrafi dedicati all’ANOVA.

 

Anche nel caso del c², se e solo se il test risulta significativo, è utile chiedersi tra quali proporzioni la differenza sia significativa.

Limitando la presentazione alle metodologie più diffuse e più semplici dei confronti a posteriori, è possibile ricorrere a

-          la procedura SNK (Student-Newman-Keuls) o di Tukey per confronti singoli,

-          il test di Dunnett per il confronto di ogni trattamento con il controllo.

 

I metodi sono simili a quelli già presentati nell'analisi della varianza. Tuttavia, trattandosi di proporzioni (p_i), si presentano due problemi.

Il primo è come rendere le varianze omogenee, poiché esse dipendono strettamente dal valore delle proporzioni (s² = npq) e sono indubbiamente differenti se il test sulle proporzioni è risultato significativo. Si ottengono varianze omogenee attraverso la trasformazione angolare, cioè delle proporzioni in gradi. Anche in questo caso, le proposte sono numerose.

La trasformazione più diffusa è quella classica in

 

 

Nel 1948 F. J. Anscombe per risposte binarie come sono le proporzioni (vedi The trasformation of Poisson, binomial and negative binomial data pubblicato su Biometrika vol. 70, pp.: 227-234) ha proposto

 

Nel 1950 M. F. Freeman e J. W. Tukey (vedi Transformations related to the angular and the square root pubblicato su Ann. Math. Statist. vol. 21 pp.: 607-611) hanno proposto

 

 

Per calcolare la significatività del confronto tra la frequenza (trasformata in gradi) del generico gruppo A con quella del generico gruppo B si utilizza una formula analoga al test t per due campioni indipendenti, utilizzando la distribuzione del q studentizzato

 

 dove

-          a/2 è la probabilità prefissata in una distribuzione bilaterale (per il test di Tukey),

-          ¥ è il numero di osservazioni in campioni grandi,

-          k è il numero di gruppi a confronto (differente tra Tukey e Dunnett, dipendendo dal numero di confronti da effettuare).

 

Il secondo problema è come stimare l'errore standard (es), avendo un solo dato (la proporzione p_i) per ogni campione. In questo caso, la relazione tra proporzione e varianza diventa un vantaggio poiché, dopo la trasformazione angolare o in gradi, la varianza è una costante e quindi l'errore standard si diversifica solo sulla base del numero n di osservazioni.

 

Per la stima dell'errore standard,  espresso in gradi,

A) per il test di Tukey

-          nel caso di campioni bilanciati di dimensioni n la formula è

 

 

-          nel confronto tra due generici campioni A e B di dimensioni n_A e n_B è

 

 

 dove 820,7 è ricavato da (180° / 2p)².

 

B) per il test di Dunnett, trattandosi di un test unilaterale

-          nel caso di campioni bilanciati di dimensioni n la formula è

 

 

-          nel confronto tra due generici campioni A e B di dimensioni n_A e n_B è

 

 

ESEMPIO 2 (i dati e lo sviluppo dell'esempio, applicati all'analisi di un ambientalista, sono tratti dal volume di J. Zar del 1999 (Biostatistical Analysis, 4^th ed. Prentice Hall, New Jersey, a pag. 564).  Rilevatori di inquinamento atmosferico per varie sostanze, collocati in quattro zone ritenute rappresentative della situazione generale di una città, hanno permesso di stimare quanto volte le misure effettuate hanno superato i livelli di attenzione

 

 

 

Valutare

-          se tra le quattro aree esiste una differenza significativa nella proporzione delle misure che hanno superato il livelli di attenzione,

-          tra quali aree esiste differenza significativa.

 

Risposta. Dapprima si deve stimare la significatività delle differenze tra le quattro proporzioni.

Con

 

 

 

 si ottiene un c²  = 8,91 con 3 gdl. Poiché i valori critici corrispondenti sono 7,815 per a = 0.05 e 9,348 per a = 0.025, al valore calcolato corrisponde una probabilità compresa tra 0.05 e 0.025.

Si rifiuta l'ipotesi nulla ed è possibile chiedersi tra quali proporzioni la differenza sia significativa.

 

A questo scopo,

1 - dapprima si ordinano le proporzioni in ordine crescente

 

 

 

2 -  successivamente le proporzioni devono essere trasformate in gradi.

E' possibile utilizzare la formula che ricorre a X e n

 

 

 ottenendo i risultati riportati nell'ultima riga della tabella successiva

 

 

 

Ad esempio, applicata al campione C

 

la proporzione p = 0,200 trasformata in gradi diventa 'p = 26,85.

 

3 -  Per avere una visione generale delle analisi, è conveniente costruire un'altra tabella. In essa, si elencano tutti i possibili confronti (prima colonna della tabella successiva) in gradi, iniziando da quello che determina la differenza maggiore; per ogni confronto si riporta anche

-          la differenza (in valore assoluto) espressa in gradi (seconda colonna),

-          l'errore standard della differenza espressa in gradi (terza colonna),

-          il valore di Q calcolato (quarta colonna),

-          il valore critico di Q_{a/2, n, k} con la probabilità a bilaterale, i gdl del test (n) e il numero di gruppi (k) (quinta colonna),

-          la significatività della differenza (sesta colonna)

 

 

 

4 - Per i confronti che si effettuano, si stima l'errore standard con

 

 

Ad esempio, nel caso del 1° confronto C vs. B

 si ottiene 2,98

 

5 - Con

 si stima il valore di Q; nel caso del 1° confronto C vs. B

 

Q risulta uguale a 4,137.

 

6 - Il valore critico corrispondente della distribuzione Q alla probabilità a = 0.05 bilaterale, con un numero di osservazioni molto alto (¥) e per 4 gruppi (fornito dalla tabella relativa), è uguale a 3,833. E' possibile rifiutare l'ipotesi nulla; la differenza tra la proporzioni minore e quella maggiore risulta significativo

 

7 - Si passa al confronto successivo, cioè tra due proporzioni che determinano una differenza minore

-          la differenza tra la proporzione prima (C = 26,85) per rango rispetto alla terza (A = 37,42) determinano un valore di Q = 3,378: non risulta significativa;

-          la differenza tra la proporzione seconda (D = 37,18) per rango rispetto alla quarta (B = 39,18) determinano un valore di Q = 0,448: non risulta significativa;

 

8 - Per il principio di cautela, tutte le differenze successive (minori di queste due, con i ranghi compresi nell'intervallo precedente) non potranno essere significative.

In conclusione il test tra le 4 proporzioni è risultato significativo. Tra tutti i possibili confronti singoli, solo quello tra la proporzione minore (C = 200) e quella maggiore (B = 0,398) è significativo.