LA REGRESSIONE LINEARE SEMPLICE

 

 

16.16.   LA PREDIZIONE INVERSA O PROBLEMA DELLA CALIBRATURA: STIMARE IL VALORE MEDIO E L’INTERVALLO DI CONFIDENZA DI X PARTENDO DA Y.

 

 

Stimata la retta sulla base la relazione logica tra causa ed effetto, come può essere la dose (X) di un farmaco e la risposta (Y) biologica indotta, non è rara la richiesta di ricorrere alla stima inversa o predizione inversa. Soprattutto quando si valuta l’effetto di un qualsiasi principio attivo, in varie situazioni si vuole

-  determinare quale sia la dose da somministrare per ottenere l’effetto desiderato.

Si parte quindi da un valore  dell’effetto o della variabile dipendente, per stimare la dose  della variabile indipendente, che mediamente lo determina (come nella figura successiva, anche se utilizza   ripetute per ogni , che è presentato in un paragrafo successivo)

 

E’ la predizione inversa (inverse prediction) o problema della calibratura (calibration).

La formula di tale relazione tra X e Y può essere ricavata facilmente dalla formula generale della retta ricavata a partire da

 per iniziare al contrario dall’effetto

 e da esso stimare la dose  che lo causa.

Più frequentemente si parte dalle relazione che utilizza i valori medi (, ), più facili da ricavare direttamente dai dati di quanto sia possibile per l’intercetta ,

 quindi da

 per ricavare con

 il valore di  dal valore prescelto di .

 

ESEMPIO 1 (DATI BIOLOGICI).  La regressione lineare tra peso ed altezza su un campione di giovani donne ha determinato la retta

 che può essere scritta anche come

Stimare l’altezza (teorica o media) di una giovane donna, con peso uguale a 60 Kg.

 

Risposta.

A)  Mediante la relazione

 dove

 = 60,0        = -73,35         = 0,796

si ottiene

 

un’altezza media di 167,5 cm.

 

B) Mediante la relazione

 dove

 = 0,796        = 172,0        = 60,0         = 63,57

si ottiene

 lo stesso risultato di 167,5 cm.

(In cm. perché è la scala con la quale è stata stimata la relazione con il peso, espresso in Kg.).

 

ESEMPIO 2 (DATI CHIMICI). La regressione inversa è utile soprattutto con dati chimici quando, ad esempio, si voglia misurare la concentrazione di una sostanza a partire dalla sua luminescenza e in analisi cliniche o farmacologiche, quando si voglia stimare la quantità di principio attivo da somministrare, partendo dall’effetto desiderato.

Dai dati della regressione tra concentrazione e fluorescenza

 

 

 

 

 dai quali sono state ricavate le statistiche

 = 1,5         = 1,93          = 6,0            = 13,1

mediante la regressione inversa stimare

- il valore della concentrazione  corrispondente al valore di fluorescenza  = 22,0.

 

Risposta.

A)  Mediante la relazione

si ottiene

 una concentrazione media  = 10,6.

 

B) Mediante la relazione

si ottiene

 sempre una concentrazione stimata  =  10,6.

 

Di questo valore medio o stimato  è possibile calcolare i limiti dell’intervallo di confidenza.

Ma non sempre questi limiti esistono.

La condizione di esistenza dei limiti di calibratura

 è

 dove

-  è il valore critico con gdl = n-2.

 

Per il calcolo dell’intervallo di confidenza della calibratura, i testi propongono formule differenti.

Nei testi di livello internazionale più reventi, l’argomento è riportato nel volume di Robert R. Sokal e F. James Rohlf del 2003 BIOMETRY. The Principles and Practice of Statistics in Biological Research (3^rd ed., eighth printing, Freeman and Company, New York, XIX + 887 p.) nelle pagine 491 - 493.

E’ illustrato anche nel testo Biostatistical Analysis di Jerrold H. Zar (4^th ed. 1999, Prentice Hall, New Jersey. In questo ultimo volume, l’intervallo di confidenza di  non è simmetrico, diversamente dall’intervallo di  ottenuto a partire da X.

 

I estremi L₁ e L₂ dell’intervallo di confidenza di  sono ricavati dalla formula

 

 dove

-   oltre alla simbologia consueta,

-    è un valore che dipende dalla probabilità a e dai df della varianza d’errore; può essere stimato con il valore critico t alla probabilità a bilaterale e con df n= n-2.

 

 

 oppure con il valore critico F alla stessa probabilità a e con df  n₁ = 1  e  n= n-2

 

 dove

 

ESEMPIO 3.  (DATI BIOLOGICI)  Calcolare alla probabilità del 95% l’intervallo di confidenza del valore  = 167,5 precedentemente stimato per Y_h = 60 Kg.

 

Risposta.  Con i dati del problema  = 167,5      = 60      a= 0.05

-   si devono dapprima calcolare i dati richiesti dalla formula

n = 7          = 63,57       = 172        = 16,42      = 510          = 0,1794

-  e ricavare dalle tabelle quelle dei valori critici, dove

 per a = 0.05 in una distribuzione bilaterale con df n = 5 il valore di t = 2,571

 e/o per a = 0.05  con df  n₁ = 1  e  n₂ = 5 il valore di F = 6,61 (ricordando che 2,571² = 6,61)

 

Successivamente si calcola K

 ed infine l’intervallo di confidenza

 dove

- L₁ risulta

 

 

 

 

 uguale a 147,65

 

-  L₂ risulta

 

 

 

 

 

 uguale a 182,85.

 

Rispetto al valore medio di 167,5 cm., l’intervallo di confidenza al 95% di probabilità è compreso tra

-  il limite inferiore L₁ = 147,65

-  il limite superiore L₂ = 182,85.

 

Per comprendere esattamente l’uso della predizione inversa e del suo intervallo di confidenza, è importante evidenziare i due aspetti fondamentali di questo risultato.

 

1 – La sua dimensione talmente grande da annullare l’informazione contenuta nella media  = 167,5 stimata. La risposta che il peso 60 Kg  può essere (al 95% di probabilità) quello di giovani donne che variano da una altezza di 147,65 a 182,85 cm è un intervallo così grande che comprende la quasi totalità delle donne e quindi così è vago o generico da essere inutile, privo di indicazioni effettive.

E’ l’aspetto che limita l’applicazione di questo metodo, in tutti i settori di ricerca (da quelli biologici a quelli ambientali),

-  nei quali la variabilità delle risposte e la dispersione dei dati dalla retta è grande.

 

2 – L’intervallo non è simmetrico rispetto al valore centrale (174,25):

-  il limite inferiore (147,65) dista  -26,60

-  il limite superiore (182,85) dista  + 8,60.

Nella predizione classica da X a Y gli intervalli erano tutti simmetrici, rispetto al valore .

 

ESEMPIO 4. (DATI CHIMICI) Dai seguenti dati su concentrazione e fluorescenza

 

 

 

 

 mediante la regressione inversa è stato ricavato il valore stimato della concentrazione  per il valore di fluorescenza  = 22,0 ottenendo

 

 

 una concentrazione media  = 10,6.

Calcolare il suo intervallo di confidenza alla probabilità del 95%.

 

Risposta. Dapprima

- dai dati  si devono ottenere i valori richiesti dalla formula

n = 7       = 1,93        = 13,1        = 6,0        = 0,188        = 112

 =

-  e  dalle tabelle ricavare il valore critico di :

 per a = 0.05 in una distribuzione bilaterale con df n = 5 il valore di t = 2,571

 

Successivamente, mediante

 si ottiene

e con

 

 

 si ottiene

 

 

 

 dove

- il limite inferiore è L₁ = 9,97

- il limite superiore è L₂ =11,29

 rispetto al valore medio  = 10,60.

L’intervallo risulta abbastanza piccolo, tale da essere utile per indicazioni operative sul valore ricavato con la regressione inversa. E’ la dimostrazione empirica di come

- nelle discipline chimiche e fisiche, dove gli scarti dei punti dalla retta sono piccoli, questa tecnica dimostri una utilità effettiva.

 

In alcune condizioni, il valore di partenza della regressione inversa non è un singolo valore, ma la media di  valori.

In questo caso, la stima del valore predetto  non viene praticamente modificata, anche

se la formula diventa

 

E’ invece modificata, in alcuni punti, la stima del suo intervallo di confidenza, i cui limiti sono determinati mediante

 

 

 dove, rispetto alla formula precedente per un solo dato,

1- al posto del singolo  è utilizzata la media  degli  dati

 

2 - al posto di  è utilizzata la quantità, minore, data da

 

3 - il nuovo valore   è dato da

 con  che resta alla probabilità , ma con gradi di libertà che diventano gdl =  

 

4 - il nuovo valore  è dato da

 

Tale argomento è presentato in modo più dettagliato

- nel testo di B. Ostle e R. W. Mensing del 1975 Statistics in Research (3^rd ed. Iowa State University Press, Ames Iowa, 596 p.) a pagg. 180-181;

- nel testo di G. A. F. Seber del 1977 Linear Regression Analysis (John Wiley, New York, 465 p.) a pagg. 190-191.

Ad essi si rimanda per approfondimenti.

 

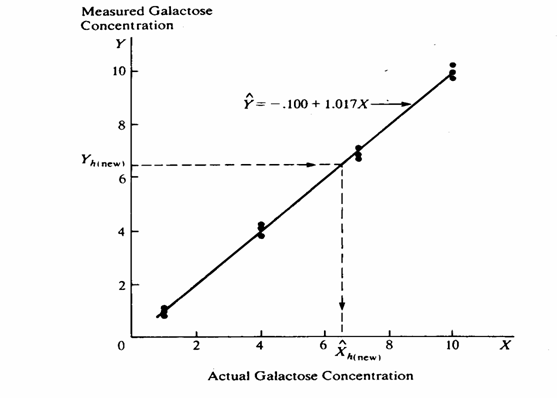
ESEMPIO 5.  (ESEMPIO DI ALTRA STIMA DELL’INTERVALLO DI CONFIDENZA DELLA REGERSSIONE INVERSA, TRATTO DA TESTO INTERNAZIONALE).  Tra i testi internazionali a maggior diffusione, la regressione inversa è presentata anche nel volume di John Neter, Michael H. Kutner, Chistopher J. Nachtsheim, William Wasserman del 1996 (Applied Linear Regression Models 4^rd ed. WBC McGraw-Hill, XV + 1408 pp.) al quale si rimanda per approfondimenti. L’esempio in esso riportato è rivolto espressamente all’analisi chimica o farmacologica; soprattutto utilizza una formula più semplice e che determina un risultato simmetrico.

 

Nell’esempio, sono stati preparati 4 campioni di farmaco, diluendo una quantità pesata esattamente (X) di principio attivo (nella figura Actual Galactose Concentration); per ognuno di essi, sono state effettuate 3 analisi chimiche (Y, nella figura Measured Galactose Concentration).

Il grafico evidenzia i 12 dati e la relazione lineare

Con essa,

-  a partire da un valore reale () di principio attivo introdotto,

-   è possibile ricavare la quantità media fornita dalle analisi ().

 

 

I risultati delle elaborazioni statistiche delle 12 misure, utili anche per i calcoli successivi sulla predizione inversa, sono:

 = 12         = -0,10         = 1,017         = 0,0272         = 135

 

 = 5,500                  = 5,492                   = 0,0142

 

Un ricercatore, che dall’analisi chimica ha ottenuto una concentrazione di 6,52 (), vuole ritornare al suo valore di partenza (),

-  per verificare se la misura ottenuta si discosta dal reale.

In questo modo, egli intende fornire una dimostrazione empirica della correttezza del metodo impiegato.

A partire dalla relazione

 ricava

 un valore stimato  = 6,51.

 

Per una analisi più dettagliata, vuole conoscere

-  l’intervallo di confidenza di questa sua stima, alla probabilità del 95%.

 

Risposta. Il testo citato, per calcolare i due valori estremi dell’intervallo di confidenza,

 propone la relazione

 

 dove

 

Con i dati dell’esempio,

 si ricava

 

 un valore  = 0,0287.

 

Poiché il valore critico della distribuzione di  di Student

- con 10 gdl e alla probabilità a = 0.05 in una distribuzione bilaterale è  = 2,228

 per l’intervallo di confidenza del valore medio = 6,51 si arriva alla stima

 

6,509 ± 2,228 ×  = 6,509 ± 0,377

 

-  del limite inferiore L₁ = 6,132 (da 6,509 – 0,377)

-  del limite superiore L₂ = 6,886 (da 6,509 + 0,377).

 

Soprattutto in queste analisi, dalla valutazione statistica è sempre importante

- passare alla interpretazione biologica e chimica del risultato.

L’errore relativo che è possibile commettere alla probabilità bilaterale del 5%

 

 

 è pari a 0,058 (5,8% se espresso in percentuale).

 Appare un valore piccolo, come in molti casi di analisi chimiche.

Ma è’ solamente l’esperto di farmacologia che a questo punto deve

-  decidere se questo errore è accettabile oppure no, se è importante oppure trascurabile per gli effetti che la differenza nelle dosi, che rientrano nell’intervallo di confidenza, può produrre sui pazienti.

E’ la stessa logica illustrata nel caso della significatività del coefficiente di determinazione R²:

- non esiste solo una significatività statistica, ma occorre porre molta attenzione agli effetti biologico o clinici della scelta.

 

Metodi statistici recenti cercano di rispondere a questa domanda di accettabilità dell’errore nelle misure, quando si confrontano due metodi per le stesse analisi chimiche e farmacologiche; è chiamato problema di calibratura (calibration).

Il quesito è:

-  “E’ possibile sostituire una stima ottenuta con un metodo classico (X), ritenuto corretto ma costoso e/o che richiede molto tempo,

-  con un metodo rapido, poco costoso, ma approssimato (Y)?”

Dopo aver stimato la regressione nella direzione classica, dalla misura precisa X a quella approssimata Y, si ritiene che il risultato sia soddisfacente se

 

 

Nell’esempio precedente

 

 si ottiene un valore inferiore a 0.001.

Secondo tale indicazione, l’intervallo di confidenza approssimato può essere ritenuto appropriato: il metodo approssimato fornisce una stima più che accettabile del metodo tradizionale.

 

Quando le stime di predizione inversa sono numerose, ognuna con il suo intervallo di confidenza, è possibile valutare se i risultati sono significativamente differenti, ricorrendo a analisi più complesse, fondate su gli stessi principi dei confronti multipli tra le medie (Bonferroni, Tukey, Scheffé, ecc.).

La regressione inversa è uno degli argomenti in cui la ricerca è ancora in una fase di sviluppo. In letteratura sono proposti svariati metodi e non esiste accordo su quale possa essere ritenuto il migliore o comunque indicato come preferibile nelle varie situazioni sperimentali.

 

Le tecniche statistiche per confrontare due metodi di misura hanno avuto uno sviluppo recente, durante gli anni ’90, soprattutto per merito di Bland e Altman. Queste tecniche, insieme con il problema della regressione least-products, ritenuta più corretta della classica regressione least-squares qui impiegata, sono presentate dettagliatamente in un capitolo successivo.