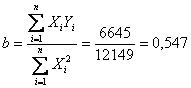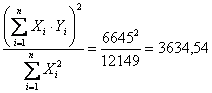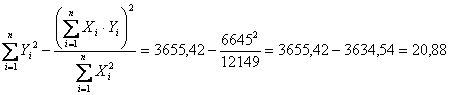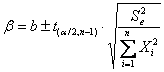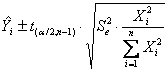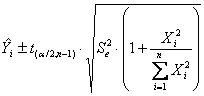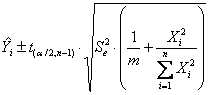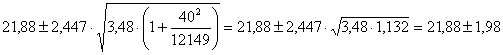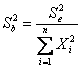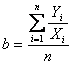LA REGRESSIONE LINEARE SEMPLICE

 

 

16.17.  LA REGRESSIONE PER L’ORIGINE: retta, INTERVALLo DI CONFIDENZA E PREDIZIONE INVERSA; VANTAGGI, LIMITI E ALTERNATiVe.

 

 

Nella ricerca applicata si presentano situazioni nelle quali

-  la relazione tra due variabili è lineare, almeno in modo approssimato, e

-  è logicamente atteso che la retta passi per l’origine,

-  cioè per il punto di coordinate  = 0   e    = 0, detto appunto origine.

 

In biologia e in medicina, è di scarsa utilità e pertanto è usata molto raramente. Negli esempi precedenti, che riguardano la relazione tra altezza e peso in giovani donne, addirittura è priva di significato reale anche il valore dell’intercetta . Come è stato banalmente evidenziato, non può esistere nessun caso in cui l’altezza sia  = 0.

Piùin generale, una retta che passa per l’origine non sempre ha un significato disciplinare. A. F. Bissel nel 1992 (con l’articolo Lines through the origin-isNO INT the answer?, pubblicato su Journal of Applied Statistics, Vol. 19, No. 2, pp. 193 – 210) ha presentato in grafico alcuni casi in cui essa è priva di senso logico e altri nei quali può essere utile.

In chimica, in fisica e in ingegneria, in molti casi in cui si confrontano due quantità e la prima è un indicatore della seconda, può appunto succedere che la retta debba logicamente passare attraverso l’origine. In altre situazioni, tale presunzione è ritenuta logica, anche quando sperimentalmente non potrà mai essere osservata: è il caso di due metodi equivalenti per la stessa analisi, quando il valore non può mai raggiungere lo zero, come in medicina il confronto tra due metodologie per determinare il livello di colesterolo o dei trigliceridi nel sangue.

 

La regressione attraverso l’origine (regression through the origin) è utile pure nel confronto tra indici o misure differenti, entrambi dipendenti dallo stesso fenomeno, come in chimica la quantità assoluta (X) di sostanza sciolta e una misura (Y) della sua concentrazione, in economia il numero di oggetti (X) e il loro costo totale (Y).

 

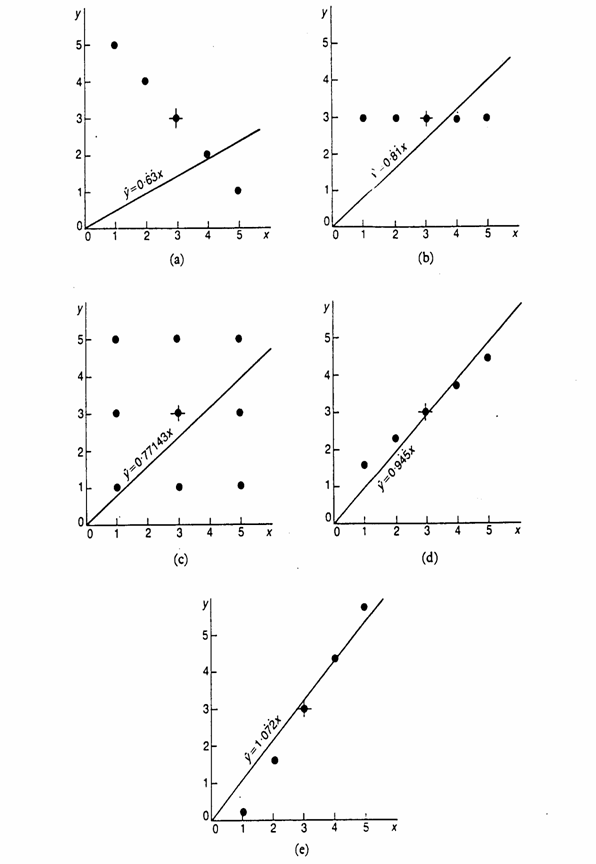
Nella pagina successiva, le cinque figure evidenziano come nelle prime tre situazioni (a, b, c) imporre alla retta di passare per l’origine determini una forte distorsione della relazione reale che intuitivamente esiste tra la variabile X e la variabile Y.

In queste figure, l’imposizione di passare per l’origine può essere adeguata per le relazioni lineari rappresentate negli ultimi due diagrammi cartesiani (figure d, e), anche se in esse si evidenzia per la collocazione della retta una leggera forzatura, rispetto alla disposizione sperimentale dei dati.

 

 

Il vantaggio di una retta passante per l’origine spesso è solo pratico:  semplifica e riduce i calcoli per

-  stimare la retta,

-  valutare la sua significatività,

-  calcolare gli intervalli di confidenza,

-  ricavare la regressione inversa.

 

Nella regressione attraverso l’origine, quindi con  = 0,

 l’equazione della retta diventa

 dove, con un campione di  coppie di dati,

-   è ottenuto dalla relazione

 

Nella successiva analisi per la significatività del coefficiente angolare (),

 con ipotesi

H₀: b = 0         contro            H₁: b ¹ 0

 si deve stimare

-   la Devianza Totale =  che ha gdl =  

 (non è misurata come al solito mediante gli scarti degli Y_i dalla loro media),

 

-   la Devianza dovuta alla regressione =    che ha gdl = 1

 

-   la Devianza d’errore ()  che concettualmente è  e ha gdl = n-1

 ma che, con formula abbreviata, è calcolata

 con

 

 

La perdita di un solo gdl (n-1) nella devianza e varianza d’errore è importante.

Essa è dovuta al fatto che il valore dell’intercetta  non è stimato dai dati, ma imposto (uguale a 0) dalle caratteristiche (vere o supposte) della popolazione.

 

Dalla devianza d’errore si ricava la varianza d’errore =

 

ESEMPIO 1. Filtrando i metri cubi di acqua () riportata nella colonna 1, sono stati estratti i Kg di deposito () riportati nella colonna 2:

 

 

 

Calcolare la retta passante per l’origine e la sua significatività.

 

Risposta. Per calcolare la retta passante per l’origine

 

 il valore di  è ricavato (vedi colonna 3 e colonna 4)

 con

 

 

 e risulta = 0,547.

 

Per la verifica della sua significatività, cioè dell’ipotesi

H₀: b = 0         contro            H₁: b ¹ 0

 si calcolano

-   la Devianza dovuta alla regressione =   

  che risulta   = 3634,54 e ha gdl = 1

 

-   la Devianza d’errore ()  che concettualmente è

 ma che con formula abbreviata (vedi colonne 3, 4 e 5) è calcolata

con

 

 e risulta  = 20,88  con ha gdl = 6

 

Riportati in tabella con la stima del rapporto F e della probabilità P ad esso associata

 

 

 

 evidenziano la altissima significatività della regressione lineare.

 

La retta di regressione passante per l’origine ha alcune caratteristiche distintive:

-   è obbligata a passare dal punto  = 0   e    = 0

-   ma non necessariamente passa per il baricentro della distribuzione (, );

-   i residui () abitualmente non sono bilanciati intorno allo zero;

-  la somma dei quadrati dei residui  può essere maggiore

 della devianza totale ;

-  di conseguenza, il coefficiente di determinazione  può essere negativo;

-  da tale osservazione deriva anche che in questo modello statistico il coefficiente di determinazione  non ha un significato chiaro.

 

Sono una serie di conseguenze che

-  la rendono molto diversa dalla retta least-squares classica,

-  ne riducono la possibilità di fornire la stessa interpretazione.

Pertanto è da evitare, quando è possibile.

 

L’intervallo di confidenza della retta di regressione passante per l’origine può essere stimato

-  sia per tutta la retta b

 

 

-   sia per il valore medio di un  determinato da un  prescelto

 

 

-   sia per un singolo valore di un determinato da un  aggiuntivo

 

 

-   sia per un singolo valore di un determinato a partire dalla media  di  valori aggiuntivo

 

 

ricordando

-  che serve il valore del t di Student alla probabilità a/2 prestabilita, per un test bilaterale,

- e che esso ha gdl  uguali a n-1.

 

 

ESEMPIO 2. Stimare i tre intervalli di confidenza alla probabilità del 95% con retta passante per l’origine calcolata nell’esempio precedente.

 

Risposta. Poiché

-   con gdl = 6 e alla probabilità a = 0.05 bilaterale il t di Student è uguale a 2,447

 = 0,547       = 3,48       = 12149

 si stimano i seguenti intervalli di confidenza:

 

1 -   per tutta la retta b

 

 dove

-  il limite inferiore è L₁ = 0,506 (0,547 – 0,041)

-  il limite superiore è L₂ = 0,588 (0,547 + 0,041)

 

2 -   per il valore medio  determinato da = 40 (scelto entro il campo di variazione sperimentale) dopo aver stimato

 

 che risulta uguale a 21,88

 

 

 si ottengono

- il limite inferiore L₁ = 20,22 (21,88 – 1,66)

 - il limite superiore L₂ = 23,55 (21,88 + 1,66)

 

3 -    per un singolo valore di determinato per= 40

 

 

 si ottengono

-  il limite inferiore L₁ = 19,90 (21,88 – 1,98)

-  il limite superiore L₂ = 23,86 (21,88 + 1,98).

 

 

In molti casi in cui si stima la retta di regressione attraverso l’origine, può essere utile anche

-  la predizione inversa.

Nel caso di un farmaco, si parte dall’effetto Y_h.

 

 

 e da esso si stima la dose  che lo causa.

L’intervallo di confidenza di tale valore  ha come limiti L₁ e L₂ determinati

 

 mediante

 

 

dove

-   oltre alla simbologia consueta,

-   è il valore predetto o stimato per un dato prescelto,

-   è un valore che dipende dalla probabilità a e dai df della varianza d’errore.

Pertanto, L’intervallo di confidenza di tale valore   può essere stimato con il valore critico t alla probabilità a bilaterale e con df n= n-1

 

 

     oppure con il valore critico F alla stessa probabilità a e con df  n₁ = 1  e  n= n-1

 

 

 dove

 

 

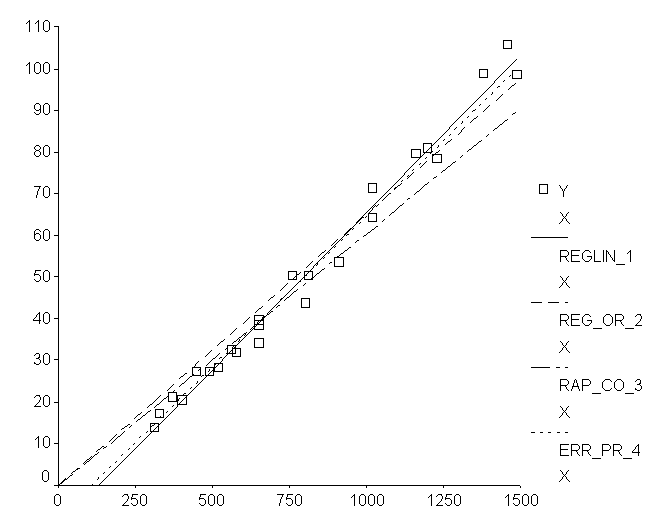
Per valutare se

-  il metodo della regressione per l’origine offre vantaggi effettivi

rispetto ad altri metodi che

-  rappresentano approssimativamente tale relazione lineare passante per l’origine o almeno vicino a essa,

 A. F. Bissel nel 1992 (con l’articolo Lines through the origin-isNO INT the answer?, pubblicato su Journal of Applied Statistics, Vol. 19, No. 2, pp. 193 – 210) ha presentato il confronto tra 4 metodi riportato nella tabella successiva

 

 

 

 dove

-   X sono i Kg di liquido che passa sopra un letto di assorbimento e

-   Y sono i Kg della quantità assorbita.

In questo esperimento è ovvio che per X = 0 necessariamente anche Y = 0.

 

Per predire i valori di Y, l’autore utilizza 4 metodi:

 

1 - la regressione lineare

 

2 – la regressione lineare attraverso l’origine

 

3 – il rapporto costante (Y/X = b)

 

 

4 – l’errore proporzionale (Y/X = a/X + b)

 

 

 

La semplice osservazione evidenzia l’accordo esistente tra i 4 metodi: ad occhio, le differenze risultano minime. Per una interpretazione corretta, è tuttavia importante fornire sia una risposta disciplinare sul significato reale delle differenze, sia una risposta statistic.

 

Criteri più oggettivi possono essere

-   l’indice di correlazione r di Pearson tra  osservato e  stimato (r(,))

-  l’errore proporzionale determinato come la radice del quadrato medio (root mean square  o rms)

 di

 

I risultati sono stati

 

 

 

 

 

 

Nel grafico,

-   la linea continua rappresenta la retta di regressione, che non passa per l’origine;

-   il tratteggio di due linee lunghe e una breve rappresenta la retta attraverso l’origine;

-  il tratteggio di due linee brevi e una lunga rappresenta la retta ottenuta con il metodo del rapporto costante; essa passa per l’origine;

-   il tratteggio con linee brevi rappresenta la retta calcolata con il metodo dell’errore proporzionale;  essa non passa per l’origine.

 

L’autore conclude affermando che ovviamente esistono altri metodi

-  sia per predire il valore di Y (coefficienti polinomiali di ordine superiore, curva di Gompertz, ecc.) con la possibilità di utilizzare i valori o loro trasformazioni, tra cui è frequente il log della dose o la duplice trasformazione log X e log Y,

-   sia per stimare l’accordo tra  gli Y osservati e quelli Y attesi (plots dei residui, studi delle differenze per valori spaziati con regolarità, ecc.).

 

Tuttavia, a suo parere, si può affermare che il valore della correlazione, che resta costante a causa della collocazione lineare dei valori, non è di alcun aiuto nella scelta. Inoltre, poiché l’errore cresce in valore assoluto all’aumentare del valore dei dati,

- l’errore proporzionale sembra essere non solo la misura più logica, ma anche quella che complessivamente riesce a prevedere in modo più accurato i valori osservati.

 

Il criterio di scelta tra i differenti metodi, come in quasi tutti i problemi di statistica, è la

-   interpretabilità entro la disciplina.

Si ritorna al problema generale: la scelta dei metodi non è solo questione di tecnica statistica, a causa della inscindibilità tra la logica statistica e la conoscenza del campo scientifico al quale viene applicata.

 

Il dibattito sui vantaggi dell’uso della retta attraverso l’origine e di eventuali metodi alternativi è sintetizzato nel testo di Peter Armitage e Geoffry Berry del 1996 (vedi la traduzione italiana curata da Mario Bolzan Statistica Medica. Metodi statistici per la ricerca in Medicina, terza ed. McGraw-Hill Libri Italia, Milano).

 

Anche nella retta attraverso l’origine, come in tutti i metodi fondati sui minimi quadrati, è condizione essenziale di validità che

-  la variabilità dell’errore sia indipendente dal valore della variabile X.

 

Ma, in particolare quando la Y assume solamente valori positivi, avviene che essa abbia varianza crescente all’aumentare della X: le soluzioni alternative più frequenti sono due.

1)  Stimare  con il rapporto tra i due totali o le due medie

 

 

 appare la stima migliore, quando la varianza () d’errore (ovviamente calcolata sulla Y) è proporzionale al valore di X.

 

Di solito avviene in conteggi, in cui X è il tempo (di durate differenti) e Y le quantità (come la radioattività) corrispondenti. I valori di Y seguono la legge di distribuzione di Poisson: a tempi (X) maggiori corrispondono quantità (Y) maggiori, che hanno varianze maggiori poiché spesso non sono costanti ma proporzionali al valore medio.

Con il rapporto indicato, si ottiene il conteggio medio per unità di tempo che elimina l’effetto evidenziato.

 

2)  Stimare  come media dei rapporti tra tutte le coppie Y/X

 

 

 appare la stima migliore, quando è

- la deviazione standard () dell’errore (ovviamente calcolata sulla Y) ad essere proporzionale al valore di X.

 

A causa dei problemi evidenziati in questa ultima parte e in precedenza, prima di utilizzare la retta attraverso l’origine è sempre utile chiedersi se essa sia realmente necessaria e se non sia possibile ricorrere a altre relazioni funzionali. Il suo uso appare ragionevole e motivato solo quando si confrontano due metodi, in campioni ripetuti, con una relazione chiara:

-   Y_i è la misura ottenuta il metodo storico o classico, attendibile ma più costoso,

-   X_i è la misura ottenuta con il metodo nuovo, meno attendibile ma rapido e economico.

(Tuttavia per affrontare il problema del confronto tra due metodi analitici sono stati proposti recentemente altri metodi, come quelli di Bland e Altman, che sono illustrati in un capitolo successivo).

Quando invece si vogliano analizzare solamente le discrepanze tra due metodi di misurazione, non vi è motivo di preferire la regressione di Y su X piuttosto che quella di X su Y e spesso è vantaggioso ricorrere a altri tipi di relazione o a trasformazione dei dati,

 quale

 

Sono approfondimenti ulteriori, per i quali si rimanda a pubblicazioni specialistiche.