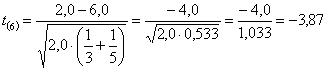LA REGRESSIONE LINEARE SEMPLICE

 

 

 

16.19.  LA REGRESSIONE PER IL CONFRONTO TRA LE MEDIE DI DUE O PIU’ GRUPPI, CON VARIABILE DUMMY; REGRESSIONE, TEST t DI STUDENT E ANOVA I.

 

 

In queste dispense, come nella quasi totalità dei testi di statistica anche di livello internazionale,

-  l’analisi della varianza e la regressione lineare sono presentati come metodi statistici distinti.

Proseguendo nell’apprendimento della statistica (vedi capitoli successivi), si impara che essi si integrano e convergono nella analisi della covarianza. Ma, leggendo i programmi dei corsi di statistica universitari anche più completi e scorrendo gli indici dei testi di statistica applicata più ampi, si ha sempre l’impressione che i due metodi servano solamente per rispondere a domande di tipo totalmente differente:

- l’analisi della varianza (e il test t di Student, nel caso di due soli gruppi) è presentata come un tecnica per testare la significatività delle differenze tra valori medi, in presenza di due o più trattamenti tra loro distinti;

- la regressione lineare è proposta come la metodologia per calcolare la relazione lineare continua che esiste tra una variabile dipendente e una variabile indipendente.

 

Pertanto, a molti ricercatori e professionisti appare strana e non facilmente comprensibile l’affermazione che

-  i problemi che possono essere affrontati con l’ANOVA possono essere risolti anche con la sola regressione lineare.

 

E’ il concetto che sta alla base del Modello Generale Linearizzato, (GLM da General Linear Model) e del suo amplio uso nell’analisi della varianza con la regressione: in molti programmi informatici, l’analisi della varianza non ha programmi specifici ma è diventata una delle possibili applicazioni dell’analisi della regressione.

Infatti, attraverso una variabile dummy,

-   per ogni individuo è possibile codificare il trattamento o gruppo di appartenenza, che quasi sempre è una variabile qualitativa,

-  in modo da renderla artificialmente quantitativa.

Quindi, con un espediente semplice ed elementare, per ogni individuo del quale

-  si possieda una misura quantitativa e l’informazione sul gruppo di appartenenza,

diventa possibile utilizzare questo ultimo dato come se fosse una variabile indipendente e così ricavare coppie di dati, utili per una equazione di regressione lineare.

Nella sua formula più semplice, una variabile dummy (dummy variable) può essere definita

- una variabile qualitativa binaria che diventa una finta variabile quantitativa, con la trasformazione dell’informazione sull’appartenenza al gruppo di controllo oppure al gruppo degli esposti in numeri, mediante la loro codifica binaria in  0  oppure  1.

 

Per dimostrare la corrispondenza dei risultati tra ANOVA a un criterio e la regressione lineare semplice, più di una lunga e complessa dimostrazione teorica è utile lo sviluppo completo di un esempio. La conseguenza più importante di questa esposizione è che la regressione lineare è uno strumento molto duttile per le analisi statistiche. Soprattutto quando si disponga di più variabili, di cui almeno una a più livelli, e si passa alla regressione multipla, che rappresenta la base della statistica multivariata.

 

L’esempio, sviluppato in tutti i suoi passaggi logici, è tratto dal testo di Stanton A. Glanz e Bryan K. Slinker del 2001 Primer of Applied Regression and Analysis of Variance (2^nd ed. Mc Graw-Hill, Inc., New York, 27 + 949).

 

I dati sono totalmente inventati e rappresentano le caratteristiche di alcuni marziani giunti sulla terra. Le numerose analisi statistiche, applicate ad alcuni parametri misurati su un campione di essi, servono appunto per scoprire le caratteristiche di questi esseri strani.

E’ un tipo di esempio che, soprattutto in passato, ha sempre suscitato la netta contrarietà dei molti statistici applicati, che avessero anche conoscenze approfondite in almeno una disciplina. Essi mai avrebbero utilizzato un esempio di pura fantasia. Impiegare esclusivamente dati reali, per essi assumeva il significato di un comportamento etico, con precise finalità didattiche, che derivava direttamente dalla costante scelta di indicare lo scopo principale della statistica: dedurre leggi scientifiche generali, a carattere biologico, ambientale, ecc.   , a partire da pochi dati campionari.

Tale approccio discende logicamente dalla convinzione che l’ipotesi da testare e l’interpretazione dei risultati statistici derivano direttamente e esclusivamente dalla conoscenza disciplinare. Ne consegue che un esempio didattico ha sempre bisogno di essere fondato sulla realtà scientifica. Inoltre è tecnicamente più credibile, poiché i dati inventati difficilmente possono avere le stesse caratteristiche di quelli reali. E come adattare la realtà dei dati al modello statistico scelto per una inferenza corretta è un altro passaggio fondamentale nell’applicazione dei metodi statistici.

Ma Glanz e Slinker, con il testo citato, hanno voluto soprattutto presentare le metodologie nel contesto di uno sviluppo logico delle potenzialità tecniche della regressione. Ed è praticamente impossibile disporre di una serie coordinata di esempi, ricorrendo a dati reali.

 

ESEMPIO con test t di Student e con ANOVA

Si assuma di voler verificare se il livello di nausea, valutato con una misura convenzionale (urp), è statisticamente differente tra un gruppo di tre marziani presi come controllo e un gruppo di cinque sottoposti a fumo passivo di sigarette.

 

I dati sono più facilmente leggibili in una tabella, uno dei metodi tradizionali di presentazione dei dati campionari, quando sono poco numerosi:

 

 

 

L’altro metodo, frequente quando i dati sono numerosi, è la rappresentazione grafica:

che meglio descrive visivamente le caratteristiche della loro distribuzione. In questo caso, per una informazione più completa, oltre ai dati sono evidenziati anche le medie e i loro intervalli di confidenza, alla probabilità a = 0.05

 

 

Per valutare l’ipotesi

H₀:         contro        H₁:

 

 mediante il test t di Student

 

 dopo aver

- calcolato le medie e il numero di osservazioni

          con  

 

          con  

 

-  calcolato le due devianze

 

 

- e ricavato la varianza comune

 

 

- si ottiene il valore del t di Student

 

 

 che risulta  -3,87 con 6

Il valore critico nella distribuzione t di Student bilaterale per a = 0.01 è t = 3.707.

Ne deriva che la probabilità è P < 0.01.

In conclusione, è possibile rifiutare l’ipotesi nulla, con un rischio a < 0.01.

 

La risposta di un programma informatico al test t di Student è:

 

 

 

I parametri riportati sono del tutto identici a quelli prima calcolati manualmente.

L’unica differenza è la probabilità P, calcolata dal computer con una precisione maggiore.

 

Applicando, agli stessi dati, per la verifica della stessa ipotesi

H₀:         contro        H₁:

un programma di analisi della varianza a un criterio, la risposta del programma informatico è:

 

 

 

 

Se confrontati quelli del test precedente, in questo ultimo risultato i parametri da considerare sono i gradi di libertà e il valore F ottenuto, vale a dire

      e      

 per la relazione

 

Inoltre è importante rilevare che il valore di P = 0.008  risulta, ovviamente, coincidente.

Per questa corrispondenza sulla probabilità P, il test t di Student deve essere bilaterale.

 

 

ESEMPIO con la regressione lineare semplice

Gli stessi dati utilizzati nell’esempio precedente possono essere interpretati e rappresentati diversamente, per applicare a essi la regressione lineare semplice,

 per la verifica dell’ipotesi

H₀: b = 0          contro          H₁: b ¹ 0

 

Per ogni individuo, la variabile classificatoria o qualitativa del gruppo di appartenenza, di tipo binario come Controlli o Esposti al fumo,

-  diventa la variabile indipendente (X) dummy: 0 oppure 1

 

 

 

 mentre la misura del livello di nausea (in urp) diventa la variabile dipendente (Y).

 

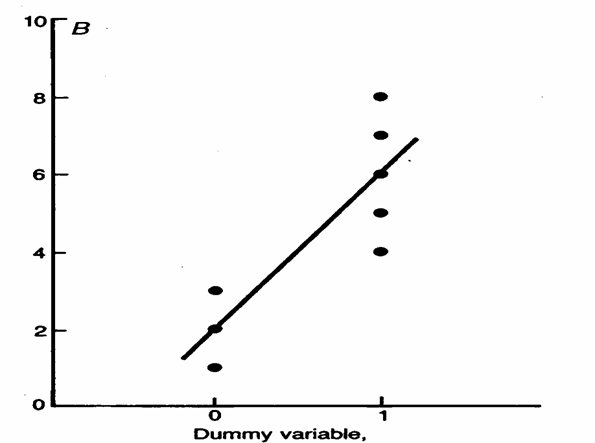
La sua rappresentazione grafica

mostra i 7 punti e come la retta di regressione

-  passi per la media delle tre osservazioni con  X = 0

-  e per la media delle cinque osservazioni con  X = 1,

 quindi attraversi la media del gruppo di controllo e quella del gruppo degli esposti

 

Con un programma informatico, l’analisi statistica dei dati per la regressione lineare

-  tra la variabile dipendente rappresentata dal livello di nausea (N da nausea)

-  e variabile indipendente rappresentata dalla quantità convenzionale di esposizione al rischio (D da dummy)

 fornisce il seguente output

 

 

 

 

E’ mostrata, con semplicità ed evidenza, la esatta coincidenza dei risultati ottenuti con le tre analisi.

 

A)   Tra i due test t di Student:

-  il primo dei dati originali dei due gruppi, per il confronto tra le due medie,

-  il secondo sulla significatività del coefficiente angolare .

 

A)   Tra le due analisi della varianza:

-  la prima sui dati dei due gruppi, per il confronto tra le due medie

-  la seconda sul linearità della regressione.

 

Pure se riferiti a parametri diversi, le conclusioni sono identiche e trasferibili da un’ipotesi all’altra per i due differenti parametri considerati:

- le due medie, in una statistica univariata;

- il coefficiente angolare, in una statistica bivariata.

E’ ovvio che, con questi dati, non conviene ricorrere alla regressione lineare per il confronto tra due medie, in quanto richiede un numero maggiore di calcoli. Ma è possibile e fornisce risultati identici

 

La generalizzazione di questa idea con un numero maggiore di trattamenti, che possono essere elaborati con più variabili dummy, porta alla regressione multipla. Per ulteriori sviluppi di questi metodi si rinvia al testo di Stanton A. Glanz e Bryan K. Slinker del 2001 Primer of Applied Regression and Analysis of Variance (2^nd ed. Mc Graw-Hill, Inc., New York, 27 + 949).