LA REGRESSIONE LINEARE SEMPLICE

 

 

16.2.   Descrizione di UNA DISTRIBUZIONE BIVARIATA

 

 

Quando per ciascuna unità di un campione o di una popolazione si rilevano due caratteri, si ha una distribuzione che è detta doppia o bivariata. I dati possono essere riportati

-  in forma tabellare,

-  in forma grafica.

 

Se il numero di dati è piccolo, la distribuzione doppia può essere rappresentata in una tabella che riporta in modo dettagliato tutti i valori delle due variabili. Esse sono indicate con

-   X e Y nel caso della regressione,

-   X₁ e X₂  nel caso della correlazione,

come nella tabella seguente:

 

 

 

Come nel caso di una distribuzione univariata, se il numero di osservazioni è grande, non è più possibile, né conveniente, fornire un lungo elenco nominativo. La sua lettura sarebbe troppo dispersiva e renderebbe impossibile evidenziare le tendenze fondamentali che caratterizzano il campione raccolto.

Si ricorre quindi ad una sintesi tabellare, chiamata distribuzione doppia di frequenze, come quella successiva.

 

Dapprima, si suddividono le unità del collettivo in modalità, livelli o classi  per entrambi i caratteri ( e ). (Modalità, livelli o classi spesso sono usati come sinonimi, anche se le modalità sono qualitative, i livelli sono quantitativi e le classi possono indicarli entrambi).

Poi si riportano

-   quelle del primo carattere (X oppure X₁) nella testata e

-   quelle del secondo carattere (Y oppure X₂) nella colonna madre

 evidenziando, nelle caselle collocate al loro incrocio,

-  il numero di misure che appartengono contestualmente ad entrambe le classi ().

 

 

 

 

I totali delle righe (N_j ) e delle colonne (M_j ) rappresentano due distribuzioni semplici e sono dette distribuzioni marginali della distribuzione doppia. E' ovvio che i due collettivi (i totali di riga e i totali di colonna) devono avere complessivamente lo stesso numero di unità, coincidente con il totale generale T.

Le frequenze riportate in una colonna o in una riga qualsiasi, come le frequenze nella colonna delle varie Y con X₂ o quelle nella riga delle varie X con Y₃, sono dette distribuzioni parziali della distribuzione doppia.

 

Quando il numero di modalità è molto grande, si può ricorrere al raggruppamento in classi. E’ effettuato in modo indipendente per le due variabili, con i metodi già descritti per una sola variabile nel I capitolo sulla statistica descrittiva. Non è assolutamente richiesto che il numero di classi o il passo siano uguali sia per la testata che per la colonna madre: le due variabili sono trattate in modo simultaneo, ma come due distribuzioni indipendenti.

 

Una distribuzione doppia di quantità può essere rappresentata graficamente in vari modi.

I metodi più frequentemente utilizzati sono due:

1 -   gli istogrammi, quando si riportano le frequenze dei raggruppamenti in classi; il metodo è uguale a quello utilizzato anche nelle distribuzioni di conteggi con dati qualitativi, come già dimostrato nelle tabelle  del test ;

2 -   il diagramma di dispersione (chiamato anche scatter plot) quando le singole coppie di misure osservate sono rappresentate come punti in un piano cartesiano. Si ottiene una nuvola di punti, che descrive in modo visivo la relazione tra le due variabili. E' particolarmente utile con valori continui, quando i dati sono misurati in scale d'intervalli o di rapporti.

 

 

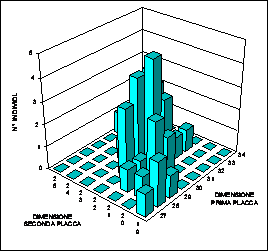
ESEMPIO 1  (TABELLA E ISTOGRAMMA).

Lo studio e la classificazione tassonomica di varie specie di Macrobiotidi si fonda sia su aspetti qualitativi sia sui rapporti tra gli arti ed i loro segmenti. Di norma, si ha una bassa variabilità entro la stessa specie e una forte variabilità tra le specie.

Per 45 animali presumibilmente della stesso gruppo Macrobiotus hufelandi, ma con forti dubbi sull'attribuzione alla specie per le difficoltà di classificazione dovute alla compresenza di giovani ed adulti difficilmente distinguibili, sono state misurate al microscopio le dimensioni (in m) di varie parti dello scheletro; tra esse le dimensioni della prima e della seconda placca, che sono state riportate nella tabella seguente.

 

 

 

 

Prima di analizzare la relazione esistente tra le due misure con i metodi dell'inferenza, è utile fornire una descrizione tabellare o grafica dei valori rilevati.

Per evitare una o più pagine di numeri di difficile interpretazione, l'elevato numero di osservazioni impone il ricorso ad una rappresentazione più sintetica, che può essere ottenuta con una tabella. Per la suddivisione in classi

-  dei valori della prima variabile (riportata in testata)

-  e dei valori della seconda (riportata nella colonna madre),

 si formano le distribuzioni di frequenza, con modalità analoghe a quelle della statistica univariata.

 

Quando le caselle sono eccessivamente numerose per essere riportate in una tabella di dimensioni unitarie, come quella successiva, si ricorre al raggruppamento in classi di una sola variabile o di entrambe.

 

 

 

Per esempio,

-  se le misure in mm della prima placca avessero avuto un campo di variazione da 26 a 60 (quindi con un intervallo di 35 mm)

-  e quelle della seconda placca da 15 a 49 (quindi con un intervallo di 35 mm),

 non sarebbe stato conveniente formare una tabella con 1225 caselle, di dimensioni 35 x 35.

Il numero di caselle sarebbe stato di gran lunga più alto del numero di individui che formano il campione, con il risultato che la quasi totalità delle caselle sarebbero state vuote e solamente alcune avrebbero avuto frequenze molto ridotte, spesso una sola osservazione.

Per ottenere un effetto di raggruppamento dei dati ed una distribuzione tendenzialmente normale, si devono formare 4 o 5 raggruppamenti, sia per una variabile che per l’altra, con 16-25 caselle in totale.

 

La tabella fornisce una prima serie di informazioni elementari, presentate nel capitolo sulla statistica descrittiva. Con le misure riportate nell'esempio, la semplice lettura della tabella evidenzia come a valori crescenti della prima variabile corrispondano valori in aumento anche nella seconda. I dati risultano concentrati lungo la diagonale, sottolineando come la distribuzione facilmente non sia casuale.

Se le due variabili fossero state totalmente indipendenti, le 45 misure sarebbero risultate disperse in tutta la tabella, con un addensamento a forma circolare od ellissoidale verso il centro.

La forma circolare o ellissoidale sarebbe dipesa dalle loro varianze, se uguali oppure differenti.

 

Gli istogrammi di una distribuzione bivariata, di semplice realizzazione con programmi informatici, presentano alcuni inconvenienti rispetto a quelli che sono utilizzati per una sola variabile (vedi la Statistica descrittiva per le distribuzioni univariate).

 

 

     

 

 

Le figure evidenziano le caratteristiche fondamentali, che appaiono di lettura più facile e immediata rispetto alla tabella, con le altezze che sono proporzionali alle frequenze riportate nelle caselle.

In realtà, come la foto di un quartiere formato da grattacieli ripresi da una strada diversa, non è una rappresentazione oggettiva: si deve scegliere un angolo di visuale, che mostra i dati in prima linea, ma nasconde quelli collocati dietro gli istogrammi più alti.

I due istogrammi bidimensionali riportati nella figura precedente sono stati costruiti utilizzando gli stessi valori tabellari.

Gli istogrammi appaiono diversi e sarebbe possibile costruirne altri ancora, visivamente differenti da questi e tra loro, partendo da angolazioni differenti della tabella (in questo caso, è stata invertita la scala per la I placca).

E’ quindi una rappresentazione da evitare se, partendo dagli stessi dati, è possibile fornire impressioni differenti sulle loro caratteristiche statistiche.

 

 

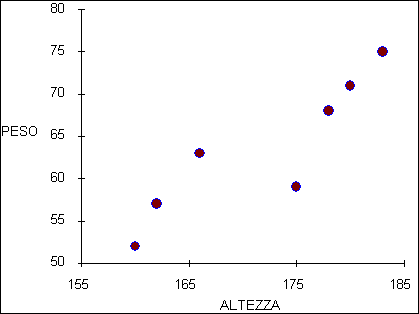
ESEMPIO 2  (DIAGRAMMA DI DISPERSIONE).

Quando i dati sono espressi in una scala continua, è conveniente una rappresentazione grafica mediante diagramma di dispersione.

La coppia di dati riferiti ad ogni individuo

- sono riportati su un grafico bidimensionale ed indicati da un punto,

- le cui coordinate corrispondono al valore di X sull'asse delle ascisse e di Y su quella delle ordinate.

Con le misure di peso (in Kg.) e di altezza (in cm.) di 7 giovani, come riportato nella tabella,

 

 

 

 

 è possibile costruire il diagramma, detto diagramma di dispersione:

 

 

 

 

Esso evidenzia, con chiarezza ed immediatezza maggiore di quanto permetta la sola lettura dei dati, la relazione esistente tra le due variabili,

-  sia nella sua tendenza generale, indicata da una retta (al crescere di una variabile aumenta linearmente anche l’altra),

-   sia nella individuazione dei dati che se ne distaccano (come l’individuo 6 di altezza 175 cm. e 59 Kg. di peso).

 

La retta che viene in essa rappresentata ha 3 scopi:

1 -  descrivere la relazione complessiva tra X e Y,

2 -  controllare i valori anomali, che diventano più facilmente individuabili,

3 -  predire la variabile Y, corrispondente a un valore X_i specifico.

 

Il grafico può essere costruito anche con centinaia o migliaia di punti.

La chiarezza del grafico dipende solamente dalla dimensione dei punti, che ovviamente deve essere inversamente proporzionale al loro numero. Il disegno risulta ugualmente chiaro e il grafico leggibile, sia quando i dati sono pochi, sia quando sono numerosi.

 

Nel caso di rappresentazione di dati riportati originariamente in tabella di frequenza, nel diagramma di dispersione il diverso numero di ricorrenze può essere indicato da simboli convenzionali. Una modalità usata con frequenza è la costruzione di più cerchi concentrici o con superfici differenti, in cui il numero di cerchi e/o le loro dimensioni sono proporzionali al numero di dati che si vuole rappresentare.