LA REGRESSIONE LINEARE SEMPLICE

 

 

16.6.   VALORE PREDITTIVO DELLA RETTA DI REGRESSIONE: ESTRAPOLAZIONE O INTERPOLAZIONE?

 

 

La retta di regressione è usata a scopi predittivi:

-  stimare i valori medi di una variabile , corrispondente a uno specifico valore dell’altra .

Ma si pongono almeno due problemi, in merito alla attendibilità o precisione della risposta.

 

1 -  I punti più vicini alla media delle , quindi al baricentro della distribuzione (), determinano stime di  che sono più precise di quelle collocate più lontano. L’intervallo di confidenza dei valori predetti, discussa in un paragrafo successivo,  fornisce una misura quantitativa di questa diversa attendibilità. Seppure in una ottica differente, il problema è approfondito in un altro capitolo, discutendo sulla individuazione dei valori anomali nella statistica bivariata e del leverage.

 

2 – Il secondo problema è rappresentato dall’individuazione dei limiti entro i quali la risposta può essere considerata tecnicamente corretta e accettabile. In altri termini, se si deve fare solo l’interpolazione oppure se è possibile anche utilizzare anche l’estrapolazione.

Interpolazione è la predizione di  entro i valori della  che sono serviti a calcolare la retta di regressione. Se la significatività della retta è dimostrata, l’interpolazione è sempre corretta.

Estrapolazione è la predizione di  fuori dai valori della . Questi risultati devono essere considerati statisticamente inattendibili, poiché non esiste alcun modo per verificare se la retta calcolata sia valida in un campo esterno ai valori osservati.

 

Nella ricerca applicata, spesso viene dimenticato che,

-  sotto l’aspetto statistico, qualsiasi previsione o stima di Y è valida solamente entro il campo di variazione sperimentale della variabile indipendente X.

 

L'ipotesi che la relazione stimata si mantenga costante anche per valori esterni al campo d’osservazione è totalmente arbitraria. Pertanto estrapolare i dati all’esterno del reale campo d’osservazione è un errore di tecnica statistica, accettabile solamente nel contesto specifico della disciplina studiata, a condizione che siagiustificato da una maggiore conoscenza del fenomeno.

In alcuni casi, questo metodo è utilizzato appunto per dimostrare come la legge lineare trovata non possa essere valida per valori inferiori o superiori, stante l’assurdità della risposta.

 

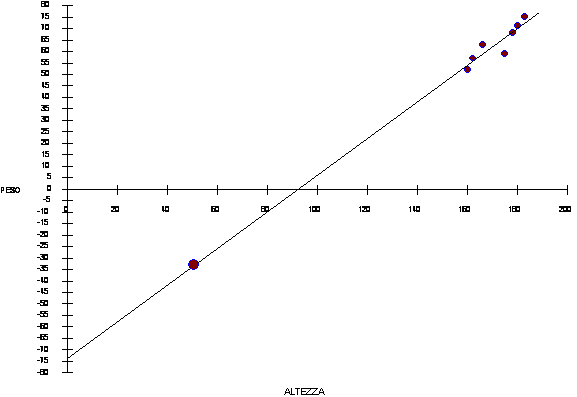
Nell'esempio 1 del paragrafo precedente, la relazione trovata tra Y e X con la retta di regressione è valida solamente per ragazze con un'altezza compresa tra 160 e 183 centimetri. E' da ritenere statisticamente errato usare la retta stimata per predire valori di Y in funzione di valori di X che siano minori di 160 o maggiori di 183 centimetri.

 

Utilizzando la retta calcolata nell’esempio 1 sulla relazione tra peso e altezza in giovani donne,

_i = -73,354 + 0,796 × X_i

 si supponga di voler stimare il peso di una bambina alla nascita.

Poiché di norma ha un'altezza (lunghezza) di circa 50 centimetri,

si ricaverebbe

-73,354 + 0,796×50 = -33,6

 che dovrebbe avere un peso medio  = -33,6 Kg. 

E’ una risposta chiaramente assurda, evidenziata nella figura successiva.

 

Infatti

-   la relazione lineare calcolata per giovani da 160 a 183 cm. di altezza non può essere estesa a dimensioni diverse.

E’ intuitivo che gli effetti saranno tanto più distorti, quanto maggiore è la distanza dai limiti sperimentali utilizzati per il calcolo della regressione.

 

Tuttavia, in alcuni settori della ricerca come in ingegneria, in chimica e in fisica, dove la dispersione dei punti intorno alla retta è molto ridotta, è diventata prassi

-  accettare una estrapolazione oltre il limite di osservazione della , che si limiti a un massimo del 10% del suo campo di variazione.

Non ha giustificazioni teoriche. E’ semplicemente supposto, sulla base dell’esperienza, che la linearità sia ugualmente mantenuta.

 

Nonostante questi limiti teorici, anche in settori caratterizzati da una variabilità molto grande, l’uso della estrapolazione è frequente, anche lontano dal campo di variazione dei valori osservati.

Nelle discipline ambientali e biologiche, l’evoluzione temporale e la diffusione spaziale di un fenomeno rappresentano casi ricorrenti di uso della regressione lineare a fini predittivi, per valori di  fuori dal campo di osservazione. Sono analisi che assumono una importanza rilevante ai fini amministrativi, per proiettare (ad esempio) l’aumento o la diminuzione dei tassi di inquinamento ad iniziare da un certo momento oppure per analizzare la diffusione geografica di un inquinante a partire da una sorgente.

Anche in questi casi, può essere corretto utilizzare ugualmente la regressione. Ma la sua linearità fuori dal campo di osservazione deve essere dimostrata, mediante altre analisi disciplinari oppure solamente ipotizzata.

 

 

 

 

L’ipotesi classica è :

-  se la linearità della regressione è mantenuta oltre il campo ristretto dell’osservazione,

-  allora, per un valore della  uguale a , il valore previsto  diventa pari a …

 

In questi anni, nelle discipline ambientali una applicazione classica è la proiezione delle dimensioni del buco dell’ozono, della temperatura media mondiale, della velocità di scioglimento dei ghiacciai, dell’aumento della quantità di anidride carbonica. Dati i valori in crescita dal 1990 ai giorni nostri, si stimano la loro dimensioni future, con proiezioni lineari fino all’anno 2050 o 2100. I risultati formano la base per scenari possibili dei loro effetti.

E’ accettabile, poiché l’interesse reale è rivolto non tanto sulla precisione nella stima, quanto a dimostrare gli effetti possibili di certi comportamenti attuali.

 

Come accennato nella parte conclusiva del paragrafo precedente, soprattutto nelle discipline dove la distanza dei punti osservati dalla retta calcolata è piccola,

-  la regressione lineare è utilizzata per la regressione inversa o calibrazione.

 

In essa la variabilità della risposta aumenta sensibilmente. Ne consegue che, pure mantenendosi sempre entro il campo di variazione delle X, gli errori commessi verso il limite di osservazione delle X è molto grande, maggiore della concentrazione standard che l’analista è interessato a misurare. E’ quindi conveniente suddividere l’analisi effettuata in tante singole regressioni, costruendo campi di variazione delle X molto minori e tra loro sovrapponibili.