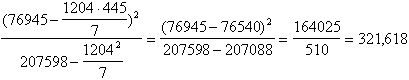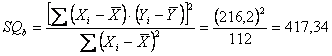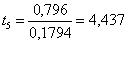LA REGRESSIONE LINEARE SEMPLICE

 

 

16.7.  Significatività' DEl coeffIciente angolare  o TEST PER la linearita’, mediante il test  e il test

 

 

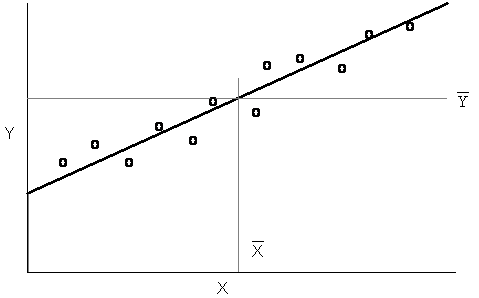
Impiegando le formule presentate, è sempre possibile ottenere una retta, con qualunque forma di dispersione dei punti.

Tuttavia, il semplice calcolo della retta non è sufficiente, per lo statistico. Infatti essa potrebbe indicare

-   una relazione reale tra le due variabili, che è realizzata quando la dispersione dei punti intorno alla retta è ridotta e pertanto i punti sono collocati molto più vicino alla retta che non alla loro media ;

-   una relazione casuale o non significativa, che è concretizzata quando la dispersione dei punti intorno alla retta non è sostanzialmente differente da quella intorno alla media  .

 

Le tre figure successive (A, B, C) rappresentano schematicamente le situazioni sperimentali tipiche.

Il concetto di significatività della retta di regressione  può essere dedotto con semplicità e chiarezza da esse.

 

La figura A riporta un diagramma di dispersione, nel quale i punti () hanno distanze dalla retta di regressione che sono sensibilmente minori di quelle dalla media (). Conoscendo , il valore stimato  mediante la retta di regressione si avvicina molto all’osservazione reale, rappresentato dal punto (). Appare logico pensare che, raccogliendo altri punti campionari, la retta calcolata resti praticamente immutata. Sono tutte affermazioni che conducono alla conclusione che

- la retta di regressione esprime la relazione reale che esiste tra i valori  e i corrispondi valori .

 

Figura A

 

 

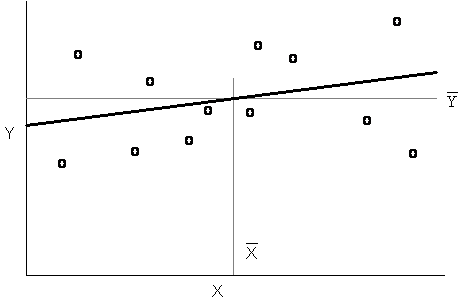
Figura  B

 

 

La figura B evidenzia una situazione opposta.

 La retta calcolata non rappresenta un miglioramento effettivo della distribuzione dei punti, rispetto alla loro media (). Ad esempio, in questo caso la retta calcolata ha una pendenza positiva. Ma sarebbe sufficiente raccogliere un'altra osservazione o estrarre un altro campione dalla stessa popolazione, per ottenere una retta differente, che potrebbe addirittura avere un coefficiente angolare  di segno opposto.

Da questa figura si può dedurre che, facilmente,

- la retta calcolata non è rappresentativa di una relazione reale tra i valori  e i corrispondi valori .

 

Il caso C raffigura una situazione intermedia tra le due presentate. Esiste incertezza sulla significatività della retta calcolata: la semplice rappresentazione grafica risulta insufficiente, per decidere in modo ragionevole se all’aumento della variabile  X i valori della Y tendano realmente a crescere.

 

 

Figura  C

 

 

Non solo in questo ultimo caso ma in tutte le situazioni, dopo aver calcolato la retta è sempre necessario ricorrere a metodi statistici che, a partire dagli stessi dati, conducano tutti alle stesse conclusioni. Sono i test di inferenza.

Per rispondere alle domande poste in precedenza, occorre valutare la significatività della retta:

-  se il coefficiente angolare  si discosta da zero in modo significativo.

Il test può essere effettuato sia mediante il test  di Fisher, sia con il test  di Student.

 

TEST  DI FISHER

Nei calcoli effettuati nei paragrafi precedenti, il coefficiente angolare  è relativo al campione.

La sua generalizzazione, quindi il valore del coefficiente angolare vero o della popolazione, è indicato con b (beta). 

 

La sua significatività è saggiata mediante la verifica dell'ipotesi nulla

 

Senza altre indicazioni più precise sulla segno della retta, rifiutando l'ipotesi nulla implicitamente si accetta l'ipotesi alternativa bilaterale H₁

 

Accettare l’ipotesi nulla e affermare che b è uguale a zero, nella regressione lineare significa che

-  al variare di X,

-  Y resta costante, uguale al valore dell'intercetta .

 

Di conseguenza, non esiste alcun legame di regressione o valore predittivo di X su Y, poiché la prima cambia mentre la seconda resta costante.

Rifiutando l'ipotesi nulla, implicitamente si accetta l'ipotesi alternativa H₁ che b sia diverso da zero: si afferma che la regressione esiste, perché conoscendo X si ha informazione non nulla sul valore di Y.

Come si vedrà successivamente presentando il test t di Student, l’ipotesi alternativa H₁ può essere anche  unilaterale. Avviene, come nell’esempio della relazione tra altezza e peso, quando è dato per scontato che all’aumentare dell’altezza il peso medio non possa diminuire e si vuole valutare se esso effettivamente cresce.

 

Per la verifica della significatività del coefficiente angolare della retta calcolata, un metodo semplice e didatticamente utile alla comprensione del significato statistico della regressione è il test F.  Esso è fondato sulla scomposizione delle devianze e dei relativi gdl, come nell’ANOVA a un criterio.

 

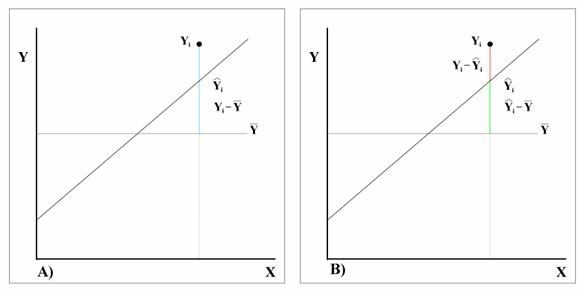
Nelle figure sottostanti A e B,

indicando con

-    il punto sperimentale,

-   _i la sua proiezione (parallela all’asse delle ordinate) sulla retta,

-    la media,

 a partire dalla somma dei quadrati delle distanze tra i tre punti ( e ) si definiscono tre devianze, come nell’analisi della varianza ad un criterio:

-  la devianza totale,  con gdl n-1,

-  la devianza della regressione o devianza dovuta alla regressione,   con gdl 1,

-  la devianza d'errore o devianza dalla regressione o residuo,  con gdl n-2.

 

Il concetto di base è che il valore stimato o predetto ,

mediante la retta

 

si avvicina sufficientemente al valore osservato .

In queste analisi sono prese in considerazione solamente i valori della variabile Y.

 

 

 

Le formule delle devianze, con i relativi gdl, sono:

- Devianza totale                                 con gdl  n-1         (Fig. A)

- Devianza della regressione               con gdl      1         (Fig. B, parte inferiore)

- Devianza d’errore                              con gdl   n-2        (Fig. B, parte superiore)

 

Queste formule definiscono il significato delle 3 devianze.

Potrebbero essere usate per stimare effettivamente i valori. Ma richiedono calcoli lunghi e forniscono risultati approssimati, poiché fondati sulle medie e sui valori della retta, che non sono quasi mai valori esatti.

Per effettuare in modo più rapido e preciso i calcoli, si utilizzano le formule abbreviate:

- Devianza totale                                con gdl  n-1

 

- Devianza della regressione                             con gdl      1

 

 ricordando che, sempre con le formule abbreviate,

 

e

 

Successivamente, per differenza, si calcola la devianza d'errore:

 

- Devianza d’errore = (Devianza totale – Devianza della regressione )      con gdl   n-2

 

Dal rapporto

-  della devianza della regressione con i suoi gdl si stima la varianza della regressione;

-  della devianza d'errore con i suoi gdl si ottiene la varianza d'errore.

 

Se l’ipotesi nulla H₀ è vera, la varianza d’errore e la varianza della regressione stimano le stesse grandezze e quindi dovrebbero essere simili.

Se invece esiste regressione, quindi  H₀ falsa, la varianza della regressione è maggiore di quella d’errore.

Il rapporto tra queste due varianze determina il valore

del test F  con gdl 1   e   n-2

F _{(1, n-2)}

 

Teoricamente, l’ipotesi nulla può essere rifiutata quando  F > 1.

In pratica, poiché in punti sono pochi, se il valore di F calcolato è inferiore al valore tabulato, relativo alla probabilità prefissata e ai gdl corrispondenti, si accetta l'ipotesi nulla:

-  la regressione lineare calcolata non è statisticamente significativa.

Al contrario, se il valore calcolato di F supera il valore tabulato, si rifiuta l'ipotesi nulla e pertanto si accetta l'ipotesi alternativa:

- tra le due variabili esiste una regressione lineare significativa.

 

Gli stessi concetti possono essere espressi con termini più tecnici.

-  Se b = 0, la varianza dovuta alla regressione e quella d'errore sono stime indipendenti e non viziate della variabilità dei dati.

-  Se b ¹ 0, la varianza d'errore è una stima non viziata della variabilità dei dati, mentre la varianza dovuta alla regressione è stima di una grandezza maggiore.

Di conseguenza,

-  il rapporto tra le varianze (varianza d'errore/varianza della regressione) con d.f. 1 e n-2 verifica l'ipotesi b = 0.

 

Il test applicato è detto anche test di linearità.

Infatti, rifiutare l'ipotesi nulla non significa affermare che tra X e Y non esista alcuna relazione, ma solamente che

-  non esiste una relazione di tipo lineare tra le due variabili.

Potrebbe esistere una relazione di tipo differente, come quella curvilinea, di secondo grado o di grado superiore.

 

ESEMPIO 1.   Con le misure di peso ed altezza rilevati su 7 giovani donne

 

 

 

è stata calcolata la retta di regressione

Valutare la sua significatività, mediante il test F.

 

Risposta. Valutare se esiste regressione tra le due variabili con il test F equivale a verificare l’ipotesi

H₀:  b = 0

 contro l’ipotesi alternativa

H₁:  b ¹ 0

 

Dopo i calcoli preliminari dei valori richiesti dalle formule abbreviate

 

               

 

 precedentemente riportate, si ottengono le tre devianze:

 

-   SQ totale  =

 

-   SQ della regressione =

 

-  SQ d’errore  = 

 

Per presentare in modo chiaro i risultati, è sempre utile riportare sia le tre devianze con i df relativi, sia le varianze rispettive, in una tabella riassuntiva

 

 

 

 

che fornisce tutti gli elementi utili al calcolo e all’interpretazione di F.

 

Con i dati dell'esempio, il valore di F

 risulta uguale a 19,59 con df 1 e 5.

I valori critici riportati nelle tavole sinottiche di F per df 1 e 5 sono

-   6,61 alla probabilità a = 0.05

-  16,26 alla probabilità a = 0.01.

Il valore calcolato è superiore a quello tabulato alla probabilità a = 0.01.

Pertanto, con probabilità P inferiore a 0.01 (di commettere un errore di I tipo, cioè di rifiutare l’ipotesi nulla quando in realtà è vera), si rifiuta l'ipotesi nulla e si accetta l'ipotesi alternativa:

- nella popolazione dalla quale è stato estratto il campione di 7 giovani donne, esiste un relazione lineare tra le variazioni in altezza e quelle in peso.

 

 

ESEMPIO 2.  E’ stata misurata l’intensità della loro fluorescenza di 7 concentrazioni (pg/ml) differenti, con i seguenti risultati

 

 

 

Verificare la linearità della regressione

 già stimata nel paragrafo precedente.

 

Risposta. Utilizzando, almeno in parte, i calcoli già effettuati per ricavare la retta, si stimano

 

- La Devianza totale delle  con

 

 

 

 

 ottenendo   = 418,28

 

-  La Devianza dovuta alla regressione, con la Devianza    = 112

  e la Codevianza   = 216,2

 ottenendo

 

 

- La Devianza d’errore (ricavata per differenza):

 418,28 – 417,34 = 0,94

 

Le devianze con i loro gdl e il risultato del test F sono riportate nella tabella

 

 

 

 

Con dati chimici, la variabilità della risposta (-) è nettamente minore di quella che si riscontra abitualmente nelle variabili biologiche. Ne deriva che la significatività della retta è nettamente superiore, come dimostrato in questo caso.

La conseguenza è che con questi dati sono frequenti altre analisi, come la calibrazione, che in biologia non vengono effettuate in quanto quasi sempre hanno un errore troppo grande e pertanto gli intervalli di confidenza sono così ampi da rendere inutile la stima dei parametri della retta.

 

 

TEST  DI STUDENT

La verifica della significatività della retta o verifica dell'esistenza di una relazione lineare tra le due variabili può essere attuata anche mediante il test t di Student, con risultati perfettamente equivalenti al test F.

Come già dimostrato per il confronto tra le medie di due campioni dipendenti od indipendenti, anche

-  nel test di linearità il valore di  con df n-2 è uguale alla radice quadrata di  

 con df 1 e n-2

     oppure    

 

Il test t è fondato sul rapporto tra il valore del coefficiente angolare  ed il suo errore standard .

La formula generale può essere scritta come

 dove

-    è il valore atteso,

-    è determinato dalla radice quadrata del rapporto tra la dispersione dei dati sperimentali (Y) intorno alla retta di regressione () e la devianza totale di X:

 

 =

 

Il test  per la linearità della regressione presenta uno svantaggio grave, ma anche vantaggi importanti, rispetto al test  già discusso.

Lo svantaggio è che è fondato su calcoli che sono didatticamente meno chiari di quelli del test , dove la devianza dovuta alla regressione () e quella di errore () hanno anche una rappresentazione grafica facilmente comprensibile.

Ma offre tre vantaggi

 

1 -   Può essere applicato anche a test unilaterali,

H₁:  b < 0      oppure      H₁:  b > 0

 che

-   non solo sono più potenti di quelli bilaterali (poiché la probabilità  è dimezzata),

-   ma spesso sono anche logicamente più adeguati e corretti ai fini della ricerca.

 

Ad esempio, sulla relazione lineare tra altezza e peso precedente analizzata,

-   è più logico un test unilaterale (all’aumentare dell’altezza il peso aumenta)

-   che non un test bilaterale (all’aumentare dell’altezza il peso varia),

 potendo a priori escludere come accettabile il risultato che all’aumentare dell’altezza il peso medio delle ragazze prese come campione possa diminuire.

 

2 -   Permettere il confronto con qualsiasi valore (b₀), (non solo con 0 come con il test F) quindi diventa possibile verificare l’ipotesi nulla

 

 ovviamente sempre con ipotesi alternative bilaterali ()

 oppure unilaterali (    oppure     )

La formula del test  può essere utilizzata per

-   verificare la significatività dello scostamento da qualunque valore atteso.

 

3 – La formula indica chiaramente che, per ottenere una regressione statisticamente significativa,

-  è vantaggioso scegliere il campione con un intervallo di variazione della  molto grande.

Nella formula precedente, è importante osservare che

-  l'errore standard di b () diminuisce, quindi il valore di t diventa più significativo,

-   all'aumentare della devianza della variabile  .

Questa osservazione ha implicazioni importanti al momento della programmazione dell’esperimento, nella scelta dei valori campionari di X.

Si supponga di dover valutare la regressione tra peso ed altezza. Si pone un problema di scegliere gli individui, ai fini di trovare una regressione significativa. Molti, non esperti di statistica, pensano che sia preferibile

-  scegliere individui di altezza media, con la motivazione che rappresentano il caso “tipico”.

In realtà, per ottenere più facilmente la significatività della pendenza della retta,

-   è sempre vantaggioso utilizzare per la variabile X un campo di variazione molto ampio,

 con più misure collocate ai valori estremi. Quindi impiegando un campione scelto non a caso, come nel confronto tra medie e tra varianze, ma osservando attentamente i dati disponibili.

Infatti

-  se la devianza di X è grande, il valore di  è piccolo;

-  di conseguenza il valore di t è grande e più facilmente significativo.

 

La varianza d'errore della retta  con df  n-2  è chiamata anche errore standard della stima.

 

E’ data da

 

Il calcolo di questa quantità è fondato sui valori attesi e quindi richiede vari passaggi matematici. Più rapidamente, può essere stimata con le formule presentate nel test , dove la devianza d'errore è ottenuta in modo rapido per differenza tra la devianza totale e quella dovuta alla regressione.

Quando sono già stati calcolati i parametri  e   della retta, è possibile ricavare

- la devianza dovuta alla regressione () direttamente dai valori sperimentali di X e Y

  mediante

 

 

 

ESEMPIO 3. Con le misure di peso ed altezza rilevati su 7 giovani donne

 

 

 

è stata calcolata la retta di regressione

Valutare la sua significatività, mediante il test  di Student

 

Risposta. E’ vantaggioso e più logico ricorrere ad un test unilaterale, quindi verificare se il peso aumenta in modo significativo al crescere dell'altezza. Tuttavia, in questo caso e solo con lo scopo di confrontare il risultato del test  con quello del precedente test , è impiegato un test bilaterale.

 

Ricordando dai calcoli precedenti che

 

       = 16,42       n = 7        = 510               

 

 il valore di  

 risulta uguale a 4,437.

Come già messo in evidenza in varie altre occasioni, il test  ed il test  forniscono il medesimo risultato. Infatti,

            corrisponde a            

(La piccola differenza tra 4,437 e 4,426 dipende dai vari arrotondamenti usati nelle due differenti serie di calcoli).

 

 

ESEMPIO 4.  Con una ricerca bibliografica, è stato trovato che il coefficiente angolare b₀ della retta di regressione tra altezza (X) e peso (Y) in una popolazione è risultato uguale a 0,950.

Il valore di 0,796 calcolato sulle 7 giovani se ne discosta in modo significativo?

 

Risposta. E’ un test bilaterale, in quanto chiede semplicemente se il valore calcolato  si discosta in modo significativo da un valore atteso, dove

H₀:  b =  0,950     e      H₁: b ¹ 0,950

Applicando la formula

si trova

t₍₅₎ =    =    = - 0,858

 

un valore  = -0.858 con 5 df.

E’ un rapporto inferiore all’unità, quindi senza dubbio non significativo.

Di conseguenza, si deve concludere che non è dimostrata l’esistenza di una differenza tra il coefficiente angolare riportato sulla pubblicazione e quello sperimentalmente calcolato con i 7 dati.

Quando non è possibile rifiutare l'ipotesi nulla in merito al coefficiente angolare  (pertanto la retta campionaria non può essere assunta come significativa di una relazione lineare tra le due variabili), la risposta ai diversi valori di X è fornita dalla media di Y, della quale può essere utile la conoscenza della varianza e della deviazione standard.

Con la simbologia ormai consueta, la varianza () e la deviazione standard () della media , sono rispettivamente

            e