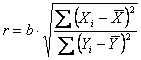LA REGRESSIONE LINEARE SEMPLICE

 

 

16.9.   LA POTENZA E LA DIMENSIONE MINIMA DEL CAMPIONE, NEL TEST DELLA REGRESSIONE: RINVIO ALLA CORRELAZIONE.

 

 

Come risulterà evidente alla fine dell’esposizione della correlazione (nei capitoli successivi), la regressione lineare semplice e la correlazione lineare semplice hanno

-  finalità differenti,

-  condizioni di validità differenti,

-  nei test di significatività verificano ipotesi differenti.

 

Nella verifica della significatività,

-  con la retta di regressione, l’ipotesi nulla verte sul valore del coefficiente angolare :

H₀: b = 0

-  nella correlazione, l’ipotesi nulla verte sul valore del coefficiente r:

H₀: r = 0

 

Quando si effettua il confronto con un qualsiasi valore teorico,

-  con il coefficiente angolare , si verifica l’ipotesi nulla

H₀: b = b₀

-  con il coefficiente di correlazione  si verifica l’ipotesi nulla

H₀: r = r₀

 anche se in questo caso occorre tenere in considerazione la non simmetria della distribuzione r.

Nonostante queste differenze, nella regressione e nella correlazione

-  la significatività può essere stimata sia con il test  sia con il test ,

-  i due test hanno gli stessi gradi di libertà (1 e n-2 per , n-2 per ),

-  le ipotesi alternative possono essere ugualmente bilaterali oppure unilaterali.,

-  i risultati della significatività sono identici; più esattamente il test  e il test  per la significatività di  forniscono lo stesso valore di quelli applicati a .

 

Sulla base di queste corrispondenze, sono uguali anche

-  la potenza a priori, cioè il numero minimo di dati () affinché il coefficiente angolare  o il coefficiente di correlazione  risultino significativi,

-  la potenza a posteriori, cioè la probabilità () di rifiutare correttamente l’ipotesi nulla, in un test sulla significatività del coefficiente angolare e del coefficiente di correlazione .

 

Di conseguenza,

- per il calcolo della potenza della regressione si può utilizzare la procedura per la correlazione, dopo aver ricavato  dai dati della regressione o da suoi indici.

 

Questo valore  può essere ottenuto a partire

 

- dal coefficiente di determinazione R² (spiegato in un paragrafo successivo)

 con

 

-  dal coefficiente angolare  e dalle due devianze

 con

 

 

Nei paragrafi successivi di questo capitolo, saranno presentati anche i metodi per

-   confrontare due coefficienti angolari e ,

 allo scopo di verificare se appartengono alla stessa popolazione, con coefficiente angolare b.

 

Anche per la correlazione, nel capitolo successivo saranno presentati i metodi per

-   confrontare due coefficienti di correlazione  e ,

 per verificare se appartengono alla stessa popolazione, con coefficiente di correlazione r.

 

 

ESEMPIO 1. (CALCOLO DI  DA ) Stima il coefficiente di correlazione  dai dati della regressione sulla relazione tra altezza e peso

 

 

 

Risposta. Con la formula

 

 dove

 dai paragrafi precedenti

 = 0,796          = 510            = 403,7

 si ottiene

 il valore .

 

ESEMPIO 2. (CALCOLO DI  DA ) Stima il coefficiente di correlazione  dai dati della regressione sulla relazione tra concentrazione e fluorescenza

 

 

 

 

Risposta. Con la formula

 dove

 dai paragrafi precedenti

 = 1,93          = 112            = 418,3

 si ottiene

il valore .

 

In questo caso, è un valore molto vicino a 1. Già il grafico di dispersione evidenziava che i punti erano collocati quasi esattamente sulla retta.