CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

 

 17.12. LA REGRESSIONE LINEARE MULTIPLA E IL MODELLO GENERALE DI REGRESSIONE LINEARE.

 

 

Negli schemi accademici, un corso di Statistica I di solito termina con la regressione e la correlazione lineare semplice. La regressione multipla e quella curvilenea rappresentano gli argomenti introduttivi in un corso di Statistica II, di norma dedicato alla statistica multivariata. Purtroppo nella preparazione culturale degli operatori e dei ricercatori nel campo ambientale e nelle discipline biologiche non si trattano mai questi argomenti, neppure in corsi di master. Come conclusione degli argomenti trattati, si introducono i concetti fondamentali dei metodi che dovrebbero essere sviluppati.

 

Il modello di base della regressione lineare multipla è simile a quello della regressione lineare semplice; se ne differenzia per l’aumento del numero di variabili predittive. Al posto di una variabile predetta o dipendente (Y) e una variabile predittiva o indipendente (X), esso ha

-  sempre una sola variabile predetta o dipendente, indicata con Y_i

-  ma due o più variabili predittive o indipendenti, indicate con X_i1, X_i2, …, X_in

 

In termini matematici, analogamente all’analisi della varianza questo modello è additivo e può essere rappresentato

 come

Y_i = a + b₁X_i1+ b₂X_i2 +    + b_nX_in + e_i

 oppure

Y = b₀ + b₁X_i1+ b₂X_i2 +    + b_nX_in + e_i

 dove

-  a oppure b₀ indicano l’intercetta,

-  b₁, b₂, …, b_n indicano il coefficiente angolare di ognuna delle n variabili  predittive X_i,

-  l’indice i segnala che la variabile dipendente e quelle predittive sono riferite allo stesso caso o individuo.

 

L’analisi statistica serve per valutare,

-  se e quanto le variabili predittive X_n insieme riescono a stimare il valore della Y,

-  quale è il contributo di ogni variabile X_n. indipendentemente dalle altre.

 

Questo modello generale di regressione lineare assume forme differenti, in rapporto al numero e al tipo di variabili predittive prese in considerazione. Tra i testi internazionali, per completezza degli argomenti e chiarezza di trattazione una sua presentazione può essere trovata in quello di John Neter, Michael H. Kutner, Chistopher J. Nachtsheim, William Wasserman del 1990 Applied Linear Regression Models (3^rd ed. 1990, IRWIN Chicago, X + 720 pp.) e nella sua versione più recente, del 1996, notevolmente ampliata negli argomenti che riguardano l’ANOVA  (4^rd ed. 1996, WBC McGraw-Hill, XV + 1408 pp.).

 

L’elenco dei modelli matematici è utile per comprendere la varietà delle applicazioni che si rifanno allo stesso schema di regressione multipla. Tra quelli maggiormente utilizzati, possono essere segnalati i seguenti 8 modelli di regressione.

 

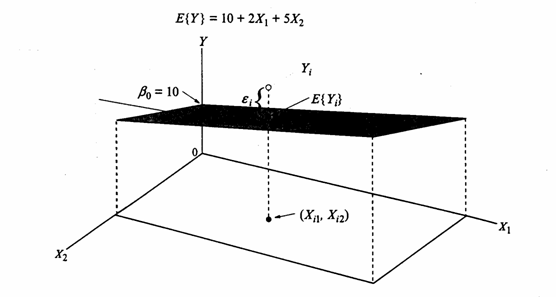
A)       Con due variabili predittive misurate con una scala di rapporti o di intervalli, si ha la forma più semplice, chiamata modello di primo ordine con due variabili predittive quantitive.

Il modello matematico è

Y_i = a + b₁X_i1+ b₂X_i2 + e_i

 

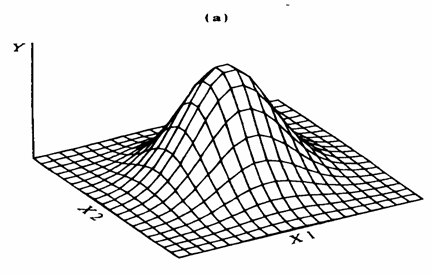
Sotto l’aspetto grafico, assume genericamente la figura di un piano che attraversa la nuvola di punti sperimentali, riportati in uno spazio tridimensionale.

 

 

 

In modo più specifico, la funzione di regressione della figura riportata è

 

Nella rappresentazione grafica sono evidenziati:

-  l’intercetta  = 10, (l’altezza di Y per X₁ e X₂ uguali a 0),

-  il piano individuato da X₁ e X₂ (che attraversa la nuvola di punti sperimentali lungo l’asse maggiore),

-  la pendenza del piano (che lungo l’asse X₁ è dato da b₁ e lungo l’asse X₂ è dato da b₂),

-  l’errore , calcolato sull’asse delle Y (è lo scarto tra il valore osservato (Y_i) e quello atteso (), indicato in alcuni testi come Y expected E).

 

Questo modello con due variabili predittive è chiamato a effetti additivi.

I parametri  b₁  e  b₂ sono chiamati coefficienti di regressione parziale perché ognuno dei due

-  riflette l’effetto parziale di una variabile predittiva sulla variabile dipendente,

-  quando l’altra predittiva è inclusa nel modello ed è mantenuta costante.

 

Un esempio semplice di regressione di questo tipo è il peso(Y_i) di una persona (i), considerando come variabili predittive l’altezza (X_i1) e l’età (X_i2).

 

B)       Con n variabili predittive, che utilizzino sempre valori misurati in una scala di rapporti o di intervalli, si ha il modello di primo ordine con più variabili predittive quantitative:

Y_i = a + b₁X_i1+ b₂X_i2 +…+  b_nX_in + e_i

 

La sua rappresentazione grafica sarebbe un iperpiano, di dimensioni n, cioè quante sono le variabili predittive considerate, in un iperspazio (poiché considera anche la Y), che non è possibile rappresentare graficamente.

 

 

C)       Una variabile predittiva può essere di tipo qualitativo.

Nel modello più semplice a due variabili prima presentato

Y_i = a + b₁X_i1+ b₂X_i2 + e_i

una variabile può essere qualitativa, come il sesso.

 

Ad esempio, è possibile stimare il peso (Y_i) di una persona (i), considerando l’altezza (X_i1) ed il sesso (X_i2). Allora la X_i1 rimane invariata rispetto al modello precedente, mentre è possibile definire che X_i2 sia

-  uguale a 1 se l’individuo è femmina,

-  uguale a 0 se l’individuo è maschio.

 

Ne deriva che la relazione per stimare i valori dipendenti ()

 cioè la funzione

-  per un maschio è

-  per una femmina è

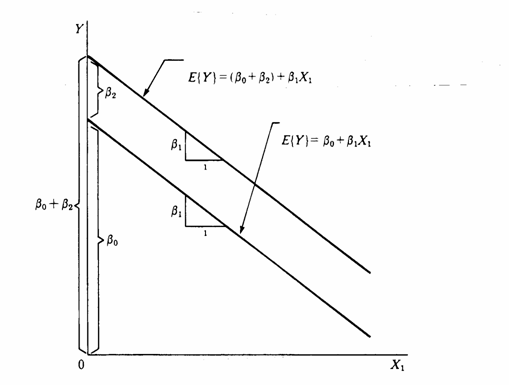
Questa ultima relazione può anche essere scritta come

 

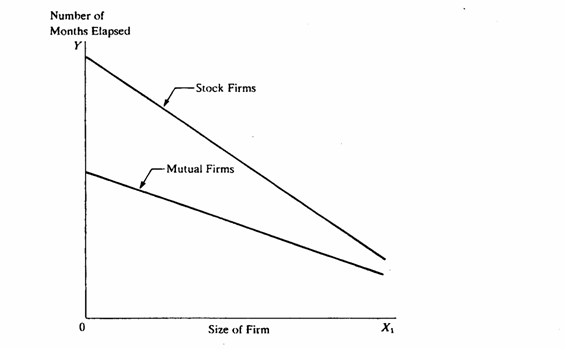
In modo generico, le due funzioni rappresentano due linee parallele, con intercette differenti.

 

 

 

D)       Mantenendo lo stesso schema, più di una variabile predittiva può essere qualitativa e/o di rango. Nel modello generale

prima presentato

Y_i = a + b₁X_i1+ b₂X_i2 +…+  b_nX_in + e_i

 

 una variabile predittiva può essere una informazione di rango, come il livello di gravità di una malattia.

Ad esempio, è possibile stimare il peso (Y_i) di una persona (i), considerando insieme con l’altezza (X_i1) e il sesso (X_i2) se l’individuo è gravemente ammalato, lievemente ammalato oppure sano, ovviamente per una patologia che influisca sul peso.

Allora, in aggiunta ai valori attribuiti alle variabili X₁ e X₂, è possibile utilizzare congiuntamente anche le variabili X₃ e X₄  attribuendo

-          X₃ = 1, se l’individuo è sano,

-          X₃ = 0, se l’individuo non è sano,

 e

-          X₄ = 1, se l’individuo è gravemente ammalato,

-          X₄ = 0, se l’individuo non è gravemente ammalato.

 

In questo caso, si ottiene la funzione

 

Y_i = a + b₁X_i1 + b₂X_i2 + b₃X_i3 +  b₄X_i4 + e_i

 

 che richiede attenzione nella interpretazione del significato di ogni coefficiente angolare.

Questa procedura di uso di più variabili è giustificata dal fatto che le informazioni di rango possono essere elaborate con maggiore facilità, quando sono scomposte in risposte binarie.

 

 

E)       Pure i modelli di regressione polinomiale possono essere interpretati come casi speciali del modello generale di regressione lineare, anche se contengono

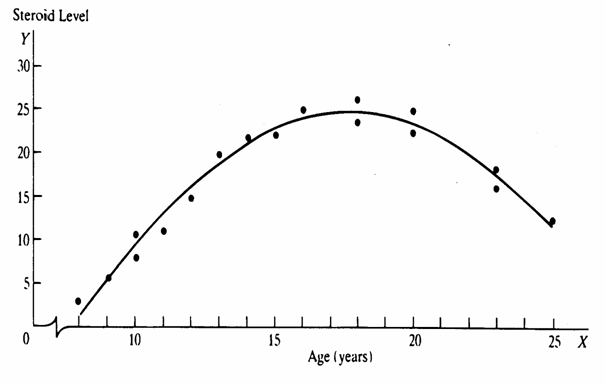
-          termini al quadrato () o elevati a potenze di ordine superiore (),

-          sia per una sola che per più variabili predittive.

Il caso più semplice può essere la quantità di steroidi (Y_i) di una persona (i) in funzione dell’età, sapendo che la variabile dipendente prima tende ad aumentare e poi a diminuire.

 

 

La sua rappresentano grafica è una funzione curvilinea, che può essere rappresentata come una curva di secondo grado su un piano cartesiano, con le stesse modalità utilizzate per la retta di regressione semplice. In questo caso specifico, il modello è

Y_i = a + b₁X_i + b₂X²_i+ e_i

 

Anche la funzione curvilinea non si allontana dal modello generale di regressione lineare. Infatti ponendo

X_i = X_i1       e      X²_i = X_i2

 si ritorna al modello generale

Y_i = a + b₁X_i1+ b₂X_i2 + e_i

 

 

F)       I modelli con variabili trasformate sono utilizzati nel caso di funzioni complesse e di risposte curvilinee di ordine superiore.

Ad esempio, quando la risposta (Y_i) è di tipo esponenziale, il modello matematico additivo può essere scritto come

logY_i = a + b₁X_i1 + b₂X_i2 + b₃X_i3 +  b₄X_i4 + e_i

 

E’ sufficiente la trasformazione

 

 per riscrivere la funzione precedente nella formula generale

 

Y*_i = a + b₁X_i1 + b₂X_i2 + b₃X_i3 +  b₄X_i4 + e_i

 

Sulla base degli stessi principi e nello stesso modo, un’altra funzione complessa

 come

 

 può essere riscritta nella formula generale

 come

 

 dopo aver effettuato la trasformazione

 

 

G)       I modelli con l’interazione tra due o più variabili predittive, come nell’analisi della varianza, presentano fattori che non sono additivi, ma moltiplicativi.

Nel caso più semplice di due variabili predittive (X₁ e X₂) che siano quantitative e presentino interazione (X₁X₂), il modello è

 

Y_i = a + b₁X_i1+ b₂X_i2 + b₃X_i1X_i2 + e_i

 

In questo caso, è sufficiente inserire una terza variabile predittiva (X₃),

tale che

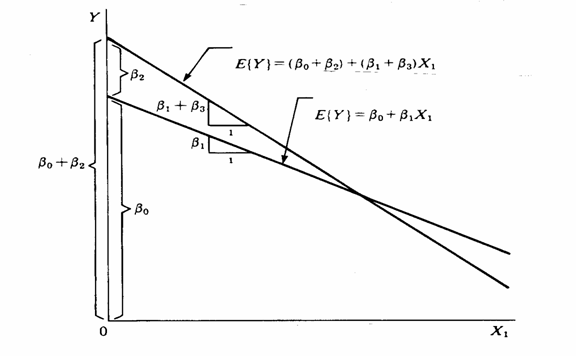
per ritornare al modello generale a tre variabili predittive

Y_i = a + b₁X_i1 + b₂X_i2 + b₃X_i3 + e_i

 

La rappresentazione grafica di questo ultimo modello è una coppia di rette che non sono parallele, come già presentato nell’analisi della varianza a due fattori.

 

 

 

 

 

 

H)       Un modello di regressione può essere molto più complesso di quelli fino ad ora presentati, in quanto costruito come combinazioni di casi.

 

Ad esempio, in un modello ancora relativamente semplice con due variabili (X₁ e X₂) quantitative, è possibile prendere in considerazione sia il termine lineare sia quello quadratico, valutando anche l’interazione (X₁X₂) tra i due termini lineari.

Tale modello scritto come

 

Y_i = a + b₁X_i1+ b₂X²_i1 + b₃X_i2+ b₄X²_i2 +b₅X_i1X_i2 + e_i

 

 dopo le  trasformazioni

 

Z_i1 = X_i1      Z_i2 = X²_i1      Z_i3 = X_i2      Z_i4 = X²_i2      Z_i5 = X_i1X_i2  

 

 può ancora essere scritto nella forma generale del modello lineare

 

Y_i = a + b₁Z_i1+ b₂Z_i2 + b₃Z_i3+ b₄Z_i4 +b₅Z_i5 + e_i

 

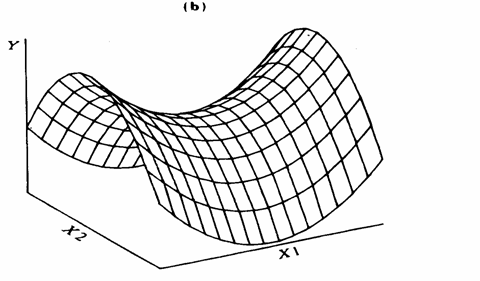
 Le due figure successive illustrano due differenti risposte complesse, che utilizzano due variabili predittive.

Da questo semplice elenco dei vari modelli di riferimento, risulta evidente che il modello generale di regressione lineare non prende in considerazione solamente risposte lineari. Il termine lineare è riferito al fatto che i parametri sono considerati additivi, mentre la risposta può essere di tipo curvilineo.