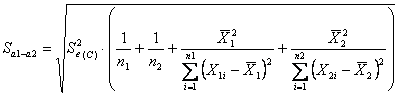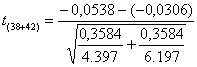CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

17.1.  CONFRONTO TRA DUE RETTE DI REGRESSIONE CON IL TEST t DI STUDENT E CALCOLO DELLA RETTA COMUNE

 

 

I coefficienti angolari delle rette di regressione possono essere posti a confronto, con concetti e metodi del tutto analoghi a quelli utilizzati per le medie.

Anche sotto l'aspetto concettuale, le rette sono medie, in quanto

-  indicano la risposta media di Y_i per un dato valore di X_i.

 

Questi test, detti di parallelismo poiché le rette con lo stesso coefficiente angolare sono parallele, servono per

- verificare la significatività delle differenze tra due o più coefficienti di regressione, mediante la distribuzione t o la distribuzione F.

 

 

 

Quando si dispone di dati di regressione che sono stati classificati in due o più gruppi, all'interno di ognuno di essi è possibile ammettere l'esistenza di una regressione lineare di Y su X. Come esempio, può essere considerato il confronto

-  della relazione  tra il peso e l'altezza in un gruppo di maschi ()

-  un altro della relazione tra il peso e l'altezza in un gruppo di femmine ()

 oppure tra più gruppi classificati per classe d’età (giovani(), adulti(), anziani()).

I dati di  gruppi, ognuno con  osservazioni sperimentali, possono essere riportati in una tabella come la precedente, utile per la presentazione dei dati e per la comprensione delle formule. In essa per ogni gruppo sono riportati i valori sia della variabile X sia della variabile Y.

 

Due o più rette di regressione possono differire per

-  la pendenza o coefficiente angolare ,

- la posizione (elevation), che rappresenta un concetto leggermente differente da quello dell’intercetta, anche se fondamentalmente coincidente

 

Mentre

-  per la pendenza il confronto utilizza i valori dei coefficienti angolari ,

-  per l’intercetta il confronto utilizza i valori ,

-  per la posizione (elevation) il confronto verifica la stessa ipotesi dell’intercetta, ma senza utilizzare il confronto tra i valori delle intercette  perché per X = 0  il valore di Y potrebbe essere privo di significato o comunque non seguire la legge lineare stimata in un campo di osservazioni lontano da esso.

Ad esempio, nella stima della relazione tra altezza (X) e peso (Y) in un gruppo di persone, non esiste una persona con altezza X = 0. Se si misura la relazione tra la capacità respiratoria (Y) in persone di varie età (X) ma sempre adulte, non è detto che la stessa relazione sia valida anche per un neonato (con X = 0).

 

Inoltre, l’uso statistico dell’intercetta  nelle discipline biologiche si scontra con il grave limite che

-  ha un errore standard molto grande, come mostrato nel capitolo precedente.

Di conseguenza, per valutare la significatività della differenza tra due posizioni (elevations), vari autori ritengono più corretto e vantaggioso ricorrere a altri metodi. Il risultato dei confronti tra rette implica scelte successive.

Se il test sulla pendenza tra più gruppi non rifiuta l’ipotesi nulla (₁=₂=₃), può essere utile stimare un coefficiente angolare comune.

Se anche il test sulla posizione non rifiuta l’ipotesi nulla (₁=₂=₃), per gli stessi gruppi si può calcolare una retta comune, che esprima la relazione tra le X e le Y di tutta la popolazione.

 

Il confronto per il parallelismo tra due rette di regressione,

-  la prima con coefficiente angolare b₁ calcolato su un campioni di dati n₁

-  la seconda con coefficiente angolare b₂ calcolato su un campioni di dati n₂

 può essere realizzato con il test t di Student, per verificare

 l’ipotesi nulla

H₀: b₁ = b₂

 contro una delle ipotesi alternative (che possono essere sia bilaterali che unilaterali)

H₁: b₁ ¹ b₂;      oppure       H₁: b₁ < b₂       oppure       H₁: b₁ > b₂

 

Questo test t di Student ha un numero di gdl = (n₁ –2) + (n₂ –2), in quanto utilizza le varianze d’errore delle due rette; spesso i gdl complessivi sono indicati come N - 4, dove N è il numero totale di osservazioni dei due gruppi.

Il valore di t_(N-4) è calcolato con

t_(N-4) =

 dove

-  è l'errore standard della differenza tra i due coefficienti angolari  e  

e è ottenuto da

 =

 dove

 

 

Se l’ipotesi nulla

H₀:

 non viene respinta, in particolare quando la probabilità P risulta alta, maggiore di 0.10 - 0.20, è accettabile assumere che i due coefficienti angolari  e  siano uguali.

 

Se si rifiuta l’ipotesi nulla, a volte è utile conoscere quale sia il loro punto di intersezione, che ha coordinate e :

- dapprima si calcola il valore di

- successivamente da esso si ricava la stima di  

 con

 oppure con

 

Quando non si rifiuta l’ipotesi nulla, molto frequentemente si richiede anche di calcolare

-  il coefficiente angolare medio  o comune  

 che è ottenuto nel modo più rapido dal rapporto tra

-  la somma delle due codevianze e

-  la somma delle due devianze di X

 

 =

 

La sua varianza  è uguale alla  riportata sopra.

Come è stata verificata l’ipotesi nulla sulla pendenza, pure con i limiti evidenziati in precedenza può essere verificata quella sulla intercetta, con l’ipotesi nulla

H₀: a₁ = a₂

 contro ipotesi alternative che possono essere sia bilaterali che unilaterali:

H₁: a₁ ¹ a₂;      oppure       H₁: a₁ < a₂       oppure       H₁: a₁ > a₂

 

Si utilizza ancora un test t, sempre con gdl = N - 4

 

 dove

 

 

 

Per stimare la significatività della differenza tra le due posizioni (elevations), con un test t che può essere sia unilaterale sia bilaterale, si può applicare (con gdl = N – 3) =

 

 dove

-   rappresenta la varianza d’errore comune, ricavata dai due gruppi (1 e 2) dei dati originari con la serie di passaggi logici e i calcoli successivi.

 

Dapprima dalle devianze e codevianze si stimano

-  

-  

-  

 

Da questi si ricavano

-   il coefficiente angolare comune

 

-   la devianza d’errore comune

 i cui gdl sono N-3

 e infine la varianza d’errore comune

sempre con gdl N-3

si applica il test t, che ha DF = N – 3(come la devianza e la varianza d'errore), con

 

 

Se le due rette a confronto non sono significativamente differenti (con una probabilità alta, non prossima al valore critico significativo)

-   né per il coefficiente angolare

-   né per la posizione (elevation)

 si può dedurre che appartengono alla stessa popolazione e quindi hanno la stessa equazione di regressione o la regressione comune:

 dove

-    è calcolato come indicato in precedenza, mentre

-    è ricavato da

 

 con   e   che sono le medie ponderate dei due gruppi

 

       e       

 

 

ESEMPIO 1.   Come dimostrazione di tutti i passaggi logici e metodologici descritti in precedenza, si assumano due campioni (1 e 2) non bilanciati di individui adulti che svolgono una attività fisica diversa, per valutare se hanno un valore di pressione sanguigna differente (Y), in rapporto all'età (X).

Sviluppando in tutti i suoi passaggi l’esempio tratto dal testo di Zar,

 

1)   i calcoli preliminari dedotti dalla serie di dati (due serie campionarie di   e  )

 hanno fornito i seguenti risultati:

 

 

 

 

2)   Da essi si ricavano i due coefficienti angolari con le loro intercette e quindi le 2 rette

 

 

 

 

3)   Per giungere al test di significatività della differenza tra i due coefficienti angolari e la posizione,

si ricavano le devianze d’errore e i df relativi

 

 

 

 e da essi si perviene alla varianza d’errore associata  o comune   che è

 

 

4)   Infine il test per il parallelismo, cioè per la verifica dell’ipotesi

H₀:       contro      H₁:

 (potrebbe anche essere unilaterale, ma in questo caso la domanda è di tipo bilaterale),

 può essere effettuato con il test t di Student

 

 

 e si ottiene (t₂₄ )=0,53

E' un risultato non significativo, poiché il valore di t calcolato (0,53) è nettamente inferiore a quello critico per a = 0.05 in una distribuzione bilaterale con gdl = 24. Anzi, il valore è addirittura vicino a quello per a = 0.5; la probabilità P così alta che si può affermare che le due rette sono parallele.

 

5)   Successivamente si passa al confronto tra le due posizioni, per verificare l’ipotesi

H₀: le due rette hanno la stessa posizione

 contro 

H₁: le due rette non hanno la stessa posizione

 

Dopo aver calcolato

-    = 1.012 + 1.659 = 2.671

-    = 1.585 + 2.475 = 4.060

-    = 2.618 + 3.849 = 6.467

 

 si ricavano

-   il coefficiente angolare comune

 =

 

-   la devianza d’errore comune

 =

 i cui gdl sono N-3, cioè 27 - 3 = 24

 

-   e infine la varianza d’errore comune

=

 

6)   Per la verifica si applica il test t con DF = N – 3 (cioè 27 – 3) = 24

 

 

 

 ottenendo (t₂₄ )=8,06.

Poiché la tabella dei valori critici per a = 0.001 bilaterale (a causa della domanda sulla esistenza della sola differenza) riporta 3,745 si rifiuta l’ipotesi nulla con probabilità P nettamente minore di 0.001.

 

7)   Si deve quindi concludere che esistono due rette di regressione, che

-   hanno lo stesso coefficiente angolare

-   ma non hanno la stessa posizione (elevation).

In altri termini, i due gruppi sono caratterizzati da due rette differenti, che hanno lo stesso coefficiente angolare  ma due intercette  differenti.

 

 

 

La rappresentazione grafica evidenzia il loro parallelismo:

- hanno coefficienti angolari  uguali, ma intercette  differenti.

 

Le statistiche delle due rette stimate sono

-   per il gruppo 1

-   per il gruppo 2

=

8)   Se l’ultimo test non fosse risultato significativo, si sarebbe dovuto concludere che esiste una sola retta di regressione, che ha

-   il coefficiente angolare comune  = 1,52

-   e la posizione di Y comune (o intercetta  comune poiché il concetto rimane valido, anche se il metodo non le ha utilizzate per il confronto).

 

Questa intercetta comune può essere calcolata a partire dalle due medie ponderate

-   delle  , cioè  

 

-   e delle , cioè

 e risulta

 uguale a 81,5.

 

In conclusione, se nessuno dei due test (il primo sulla differenza tra b, il secondo sulla differenza fra a) fosse risultato significativo,

 la retta comune sarebbe stata

      cioè    

 

Altri testi limitano il confronto delle rette ai due coefficienti angolari. Infatti l'intercetta quasi sempre non ha significato biologico. Qualunque sia il risultato statistico di b e a, è sempre importante evidenziarne l’interpretazione biologica e ambientale.

 

ESEMPIO 2.  Si confronta la capacità respiratoria (Y, misurata in litri) di 40 soggetti esposti da anni alle esalazioni di Cadmio (gruppo 1) con quella di 44 lavoratori non esposti (gruppo 2), considerando l’effetto dell’età (X, misurata in anni).

 

 1) Dalla distribuzione dei dati si ricavano le stime preliminari per il test,

 ottenendo

 

 

 

2)   Da essi si ricavano i due coefficienti angolari, con le loro intercette e quindi le due rette

 

 

 

 

3)   Per giungere al test di significatività della differenza tra i due coefficienti angolari, si devono ricavare le loro devianze d’errore (di solito con la formula abbreviata come per i calcoli riportati) e i df relativi come nella tabella seguente

 

 

 

 e da essi pervenire alla loro varianza associata  o comune  che è

 

 

4)   Infine il test per il parallelismo, cioè la verifica dell’ipotesi

H₀:       contro      H₁:

 (potrebbe anche essere unilaterale, ma in questo caso la domanda era di tipo bilaterale),

 può essere effettuato con il test t di Student

 

 

 

Poiché in valore assoluto il risultato (1,966) è minore del valore critico (1,990) riportato nella tabella del test t di Student con gdl = 80 per la probabilità a = 0.05 bilaterale,

-  non è possibile rifiutare l’ipotesi nulla.

Tuttavia, dato il numero non molto alto di osservazioni e la vicinanza al valore critico, si può parlare di significatività tendenziale.

Ancora una volta è utile sottolineare l’importanza dell’ipotesi che si vuole verificare e quindi della esatta conoscenza del problema disciplinare, che non deve mai essere disgiunta dalla conoscenza della tecnica statistica: se la domanda fosse stata di tipo unilaterale, la probabilità stimata sarebbe stata leggermente maggiore di 0.025 e quindi si sarebbe evidenziata una differenza significativa tra i due coefficienti angolari.