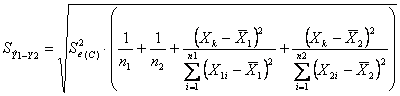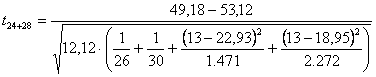CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

17.2.   CONFRONTO TRA PUNTI SU DUE RETTE DI REGRESSIONE

 

Quando nel confronto tra due rette si è rifiutata l’ipotesi nulla per uno solo dei parametri () o per entrambi, quindi si hanno due rette significativamente differenti, può essere utile

- verificare se sono tra loro significativamente differenti due punti  collocati sulle due rette differenti, ma aventi lo stesso valore di .

 

Ad esempio, nella ricerca applicata può essere chiesto di verificare

-  in medicina se la capacità respiratoria () di due persone della stessa età (), il primo appartenente al gruppo degli ammalati () e il secondo al gruppo di controllo (), sono statisticamente differenti nei loro valori medi;

-  in chimica se il volume () di due sostanze differenti (1 e 2), per le quali esiste una crescita lineare differente al variare della temperatura, è significativamente diverso alla stessa temperatura ();

-  in farmacologia se l’effetto di due farmaci ( e ) con una relazione dose - effetto differente, ma sempre di tipo lineare, è significativamente differente alla stessa dose ().

 

In termini più formali, si vuole verificare

H₀:      contro      H₁:

 con un test  che può essere sia bilaterale che unilaterale.

 

Il valore del  con df = N - 4 è

 

 dove

 

 con la stessa simbologia utilizzata nel paragrafo precedente.

 

ESEMPIO. Rielaborando i dati di Jerrold H. Zar nel testo del 1999 Biostatistical Analysis (4^th ed. Prentice Hall, Upper Saddle River, Ney Jersey XII + 663 + App. 212 pp.), si supponga di aver stimato la relazione dose - effetto di due farmaci (1 e 2)

 

 con due campioni  (1 e 2) i cui valori hanno dato

 

 

 

Si vuole sapere se per la dose  = 13, l’effetto dei due farmaci è significativamente differente.

 

Risposta.

1)   Con i valori già calcolati nei due gruppi per stimare le due rette, si ricavano le due devianze d’errore e i df relativi

 

 

 e da essi si perviene alla loro varianza associata  o comune  che è

 

 

2) Successivamente, per la dose ipotizzata (, si calcola

- l’effetto sulle diverse rette ( e ) che si vogliono confrontare

 

 = 49,18

 = 53,12

 

 ottenendo  = 49,18   e   = 53,12

 

3 ) Infine con il test

 

 

 

 si ottiene  = -2,87 con gdl = 52.

 

La tabella dei valori critici con df = 52 riporta

-   2,674 per a = 0.01 in un test bilaterale e per a = 0.005 in un test unilaterale.

Di conseguenza,

- si rifiuta l’ipotesi nulla alle due probabilità indicate.

Ovviamente tra esse deve essere utilizzata quella collegata al tipo di ipotesi alternativa che è stata formulata al momento dell’enunciazione del problema.

Ancora una volta ritorna il problema di non effettuare e un test per una significatività generica, ma in rapporto stretto con l’ipotesi che si intende verificare.