|
CONFRONTI TRA RETTE, CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA
17.3. CONFRONTO TRA PIU’ RETTE DI REGRESSIONE CON IL TEST F, CALCOLO DELLA RETTA COMUNE E INTERVALLI DI CONFIDENZA
Tutti i test attuati nei due paragrafi precedenti su due campioni indipendenti possono essere estesi al caso di più campioni. Come nel confronto tra medie, si passa dall’uso del t di Student al test F di Fisher.
La significatività delle differenze tra più coefficienti di regressione può essere verificata mediante l’analisi della varianza, con ipotesi nulla
ed ipotesi alternativa
nella condizione che - le varianze d’errore dei vari gruppi siano omogenee. I passaggi logici sono:
1) Se si assume
come vera l'ipotesi nulla che sono tra loro tutti uguali, i vari coefficienti
angolari calcolati (
2) A questo coefficiente angolare comune è associata una quota di devianza della Y (Dev.c = devianza comune) pari a
3) Per ogni j-esimo gruppo la retta di regressione è data da
Se le varie rette a
confronto possono essere considerate tra loro parallele, nello stesso modo la stima
del valore medio comune della Y (
4 ) Come riportato nel grafico precedente, lo scostamento
di ogni singola osservazione può essere diviso in tre quote: - del punto dalla
retta del suo gruppo ( - della retta del
gruppo da quella comune ( - della retta
comune dalla media generale (
5) Le rispettive devianze, ossia la somma dei quadrati di questi scarti, con k gruppi o rette a confronto e con un numero totale di osservazioni pari a N possono essere ripartite in modo del tutto simile a quanto già fatto nell’ANOVA a un criterio:
I - devianza totale entro gruppi con gdl N-k corrispondente alla somma delle devianze totali di ogni gruppo,
II - devianza residua intorno alle rette separate con gdl N-2k corrispondente alla somma delle devianze d’errore di ogni retta,
III - devianza della regressione di ogni retta con gdl k ottenuta sottraendo la 2 alla 1,
IV - devianza dovuta alla retta comune, con gdl 1 o di parallelismo, data dal rapporto tra il quadrato della somma delle codevianze e le devianze di X,
V - devianza dovuta alle differenze tra rette, con gdl k-1 o di scostamento dal parallelismo, ottenuta sottraendo la 4 alla 3.
6) Indicando - la somma dei
quadrati degli scarti di Xij rispetto alla sua media
- la somma dei quadrati degli scarti di Yij
rispetto alla sua media
- la somma dei prodotti degli scarti di X e Y rispetto alle loro medie con
il calcolo delle devianze è mostrato con semplicità.
Utilizzando, per semplicità di calcolo, le formule abbreviate si ottiene - la devianza entro gruppi con
con gdl N-k (dove k è il numero di gruppi o rette)
- la devianza dovuta alla retta comune o al coefficiente angolare comune con
con gdl = 1
- la devianza dovuta alle differenze tra coefficienti o alle differenze tra rette:
con gdl k – 1. Dal loro rapporto si ricava la varianza
dovuta alle differenze tra i coefficienti angolari (
- la devianza residua intorno alle rette separate:
con gdl N – 2k. Dal loro rapporto
si ottiene la varianza d’errore intorno alle rette separate (
7) L'analisi della varianza per verificare la significatività delle differenze tra i coefficienti di regressione è un test F con gdl k-1 e N-2k.
E’ ottenuto mediante il rapporto tra - la varianza delle differenze tra
coefficienti di regressione lineare - la varianza del residuo intorno alle
rette separate
ESEMPIO. Sviluppando un esempio riportato in un testo a grande diffusione internazionale (Armitage e Berry ripetutamente citato come testo di riferimento), si supponga di voler verificare se esiste una differenza significativa tra i coefficienti angolari di tre rette differenti, stimate nella relazione tra capacità respiratoria (in litri) e età (in anni in tre gruppi (non bilanciati) di persone diversamente esposte a fattori di rischio.
Risposta. 1) Per verificare l’ipotesi
nulla contro l’ipotesi alternativa
dalla distribuzione dei dati
sono stati ricavati i seguenti valori
2) Da essi, per
semplice somma delle devianze e delle codevianze dei vari gruppi, si ottengono
i valori totali e il coefficiente angolare comune
evidenziando che la devianza d’errore totale è
4) Da questi Totali dei k gruppi si ricavano:
I - La devianza
dovuta alla retta comune o al coefficiente angolare comune ( con
è
II – La devianza d’errore per le rette
separate ( con
è
III – La devianza dovuta alla
differenza tra i coefficienti angolari a) per sottrazione da quella d’errore totale delle due dovuta alla regressione comune e alle singole rette di regressione
44,90 – 14,86 – 27,54 = 2,50 con gdl uguali a (N – k) – 1 – (N – 2k ) = k - 1 81 – 1 – 78 = 2 cioè 3 – 1 = 2
b) dai singoli valori delle codevianze dei k coefficienti angolari e quello comune
5) Allo scopo di avere una visione generale e per meglio comprendere i successivi test F, è sempre utile costruire la tabella dell’ANOVA
Si verifica - la significatività del coefficiente
angolare comune mediante il test F
Poiché il valore critico con df 1 e 70 (78 è riportato in poche tabelle) alla probabilità a = 0.001 bilaterale è 13,3 si rifiuta l’ipotesi nulla: esiste una tendenza comune altamente significativa, nella relazione tra età e capacità respiratoria.
- la significatività della differenza
tra i k coefficienti angolari mediante il test F
Poiché il valore critico con df 2 e 70 (78 è riportato in poche tabelle) - alla probabilità a = 0.10 bilaterale è 3,13 - alla probabilità a = 0.05 bilaterale è 3,89 non si può rifiutare l’ipotesi nulla, anche se la probabilità abbastanza vicina al 5%. Si può affermare, appunto perché è collocato tra il 55% e il 10%, che - non è dimostrata ma potrebbe esistere una tendenziale differenza tra i coefficienti angolari a confronto.
E’ sempre importante osservare attentamente il grafico: la non significatività della retta potrebbe suggerire che esista una relazione di tipo curvilineo. Se questo metodo fosse stato applicato al caso precedente di due soli campioni, si sarebbe ottenuto un valore di F uguale a t2. Il confronto tra i tre coefficienti angolari è avvenuto senza calcolarli e senza stimare né rappresentare graficamente le tre rette. In varie situazioni, può essere utile pervenire anche alla stima delle rette. Per questo dalla distribuzione dei dati e dalle stime precedenti si ricavano
e con la formula generale
si stimano prima
e infine le rette
Un ulteriore aspetto importante per meglio comprendere e interpretare i risultati è il calcolo dell’intervallo di confidenza dei coefficienti angolari stimati. A questo scopo si utilizza - la varianza d’errore 0,353 con i suoi 78 gdl - il valore di t che, scelto dalla tabella con gdl = 78 e per a = 0.05 bilaterale, è uguale a 1,991 - la devianza della X del gruppo in oggetto ottenendo per ogni gruppo e in comune
il limite inferiore
Una lettura attenta degli intervalli di confidenza mostra che il coefficiente angolare del campione 3 è fuori dell’intervallo di confidenza di quello del campione 1. Ma trattandosi di confronti tra k valori, non è corretto dedurne una differenza significativa, peraltro non dimostrata con l’analisi della varianza. Per valutare tra quali coefficienti angolari la differenza campionaria sia significativa, è necessario - prima rifiutare l’ipotesi nulla con il test F tra tutti i k campioni, - successivamente ricorre ai confronti multipli, illustrati nel paragrafo successivo.
La lettura delle
età medie (
Come mostrato nel caso di due campioni, anche in quello con k campioni l’analisi statistica può essere estesa a altre caratteristiche della retta. E’ possibile confrontare - oltre ai coefficienti angolari, - le intercette o posizioni (elevations), - il valore
medio atteso su rette diverse, per la stesso valore della - e valutare se sono complessivamente uguali (test for coincidental regressions) oppure no. Per questi approfondimenti si rinvia a altri testi, tra i quali - Zar Jerrold H., 1999, Biostatistical Analysis, (fourth ed., Prentice Hall, Englewood Cliffs, New Jersey, USA, pp.663 + 203app)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
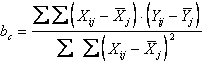


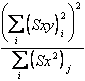
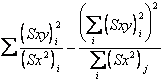
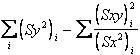
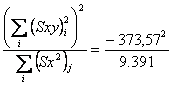 = 14,86
= 14,86