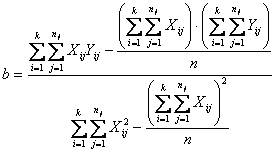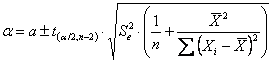|
CONFRONTI TRA RETTE, CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA
17.7. TEST DI LINEARITA’ CON Y RIPETUTE, IN CAMPIONI NON BILANCIATI
Non sempre i campioni sono bilanciati. In vari esperimenti di laboratorio e in farmacologia, può sempre succedere che almeno una cavia o un paziente non permettano di misurare l’effetto della dose somministrata. Le cause possono essere numerose, dal decesso alla mancata risposta biologica, per motivi fisiologici o genetici. L’analisi diventa meno semplice e non permette di calcolare tutti i termini della regressione, che non è più centrata sulla dose e sulla risposta medie. Nell’industria farmaceutica, la regressione lineare semplice con Y ripetute è spesso utilizzata per la convalida di metodi analitici, atti alla determinazione quantitativa di principi attivi e dei possibili degradati in forme farmaceutiche. Uno degli passaggi importanti della convalida consiste nel verificare la linearità della risposta al variare della concentrazione. Per tali test, si preparano concentrazioni scalari (almeno 5) della sostanza da quantificare, replicando un certo numero di volte (da tre a sei) la determinazione per ogni concentrazione. Nell’esempio successivo è illustrata in modo dettagliato questa metodologia, applicata al caso più generale di campioni non bilanciati.
ESEMPIO. Si assuma che per 5 concentrazioni crescenti (X) siano state effettuate misure sul tempo di efficacia (Y) di un farmaco. Per ogni dose sono state prese 5 cavie, ma per alcune non è stato possibile ottenere la risposta biologica.
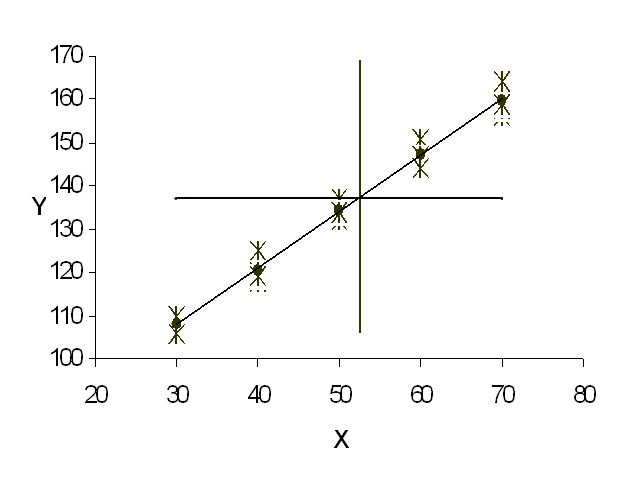
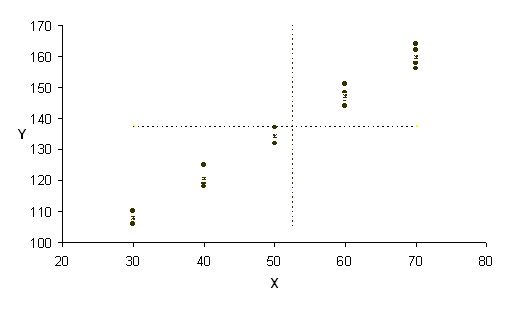
La lettura delle risposte su un grafico, come in un’analisi della varianza a un criterio, avvantaggia la comprensione delle metodologie statistiche e dei risultati delle analisi.
Si riportano tutti i valori (i punti) e le medie (asterisco) per ogni dose X. E’ utile riportare anche la media generale delle Y e delle X (le due rette tratteggiate, perpendicolari tra loro)
(Per il calcolo della somma, cioè della quantità totale del principio attivo somministrato, e della media delle X occorre considerare non solo i 5 valori riportati, ma anche quante volte le singole dosi sono state somministrate.) Si può
immediatamente osservare che le due medie generali
L’analisi della varianza a un criterio di classificazione è fondata sul rapporto tra le varianze derivate da - gli scarti delle
medie - gli scarti di ogni osservazione Utilizzando solamente i 20 valori delle Y, dopo aver calcolato - - le sommatorie delle Y per le 5 dosi: (30) = 324; (40) = 482; (50) = 403; (60) = 736; (70) = 799; si stimano - la devianza totale = ottenendo:
- la devianza tra trattamenti = ottenendo:
136,33 + 108.339,2 + 127.680,2 - 376.476,8 = 6.751,93 con gdl = 4
- la devianza d’errore ricavata per sottrazione 6.869,2 – 6.751,93 = 117,27 con gdl = 15 (19 – 4) o come devianza entro ogni gruppo. La tabella che riporta questi risultati
e quello del test F mostra una differenza altamente significativa tra le medie dei 5 gruppi.
Per calcolare la retta di regressione semplice che consideri le medie dei 5 dosaggi ricordando che
e
con i dati dell’esempio dopo aver ricavato
- - -
si stimano
e
Pertanto, la retta di regressione lineare semplice che rende minimi gli scarti al quadrato tra i punti collocati sulla retta e le medie dei gruppi è
Per disegnare la
retta sul grafico precedente, è sufficiente stimare il valore di Ad esempio, per
A partire dal punto individuato, si traccia la retta che passa attraverso il baricentro della distribuzione dei dati.
Se i calcoli sono stati effettuati manualmente, può sorgere il dubbio di aver commesso qualche errore. E’ possibile una
verifica empirica e rapida: scelto un
Dalla
rappresentazione grafica, è semplice osservare che la retta si avvicina ai
punti medi molto più della media generale delle Y. E’ la devianza dovuta
alla regressione lineare ( Tale quantità, che ha gdl = 1 è calcolata con
Con i dati dell’esempio,
si ottiene La quota di devianza
dovuta alla non linearità ( Con queste due informazioni si può completare l’analisi della varianza condotta in precedenza, ottenendo
Ricordare:
Dalla semplice lettura delle devianze si evidenzia che la devianza tra gruppi è quasi tutta imputabile alla regressione lineare. Ma è necessario verificare statisticamente questa impressione.
Il test per la linearità, cioè dell’esistenza di una relazione reale di tipo lineare tra dose e risposta richiede che siano realizzate contemporaneamente due condizioni: A) che risulti significativo il test per la linearità. B) che risulti non significativo il test per la regressione non-lineare;
Il primo è attuato dividendo la varianza dovuta la regressione lineare per la varianza d’errore; con i dati dell’esempio
Il risultato con F(1,15)
= 863,4 dimostra che la retta si avvicina ai punti individuati dalle medie
molto più della media generale
Il secondo dividendo la varianza dovuta alla regressione non-lineare per la varianza d’errore; con i dati dell’esempio
Il risultato con F(3,15) = < 1 dimostra che le curve di grado superiore non si avvicinano ai punti individuati dalle medie in modo significativo rispetto alla retta. In conclusione, la risposta è di tipo lineare
In questa verifica, può essere conveniente iniziare dal secondo test, quello per la non-linearità. Infatti, quando esso non risulta significativo, è possibile sommare alla devianza d’errore e ai gdl la quota dovuta alla non linearità, ottenendo
L’ipotesi sulla linearità H0: b = 0 contro H1: b ¹ 0 può essere verificata anche mediante
In questo caso, il risultato è ancor più significativo. Il test ha una efficienza relativa maggiore. In esso aumentano sempre i gdl della varianza d’errore, aspetto importante soprattutto quando essi sono pochi. Inoltre, in questo caso, si determina il vantaggio aggiuntivo di una varianza d’errore minore.
La capacità predittiva della retta
è superiore al 98%. Per il calcolo - dell’intervallo di confidenza di
- dell’intervallo di confidenza
della intercetta
- dell’intervallo di confidenza di
un valore medio di
- dell’intervallo di confidenza di
un singolo valore di
la varianza d’errore è e la devianza
delle X come stimata in precedenza è
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |
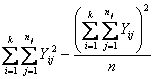 con gdl =
con gdl =  con gdl =
con gdl =