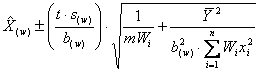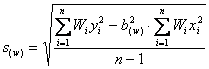CONFRONTI TRA RETTE,

CALCOLO DELLA RETTA CON Y RIPETUTE, CON VERIFICA DI LINEARITA’ E

INTRODUZIONE ALLA REGRESSIONE LINEARE MULTIPLA

 

 

 

17.8. CENNI SULLA REGRESSIONE PESATA E DELLA SUA CALIBRAZIONE

 

 

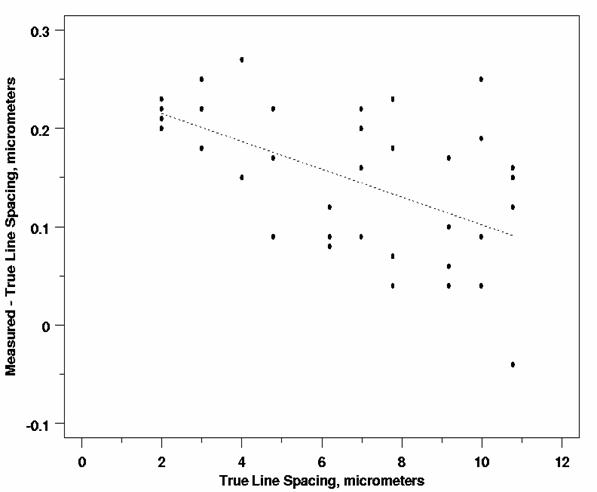
Una delle condizioni più importanti, per la validità della regressione lineare least-squares, è che

-  ogni punto deve fornire la stessa quantità d’informazione nella stima della varianza.

E’ un altro modo per ripetete l’enunciazione classica che

- la deviazione standard dell’errore deve essere costante, per tutti i valori della variabile esplicativa o indipendente.

Tale assunzione non sempre è vera e non sempre è possibile realizzarla, anche mediante la trasformazione dei dati. Ad esempio, come nella figura sottostante,

-  all’aumentare delle linee del micrometro (asse delle ascisse),

- cresce la variabilità quando le misure sono ripetute (asse delle ordinate).

 

 

 

 

  

In queste condizioni, la metodologia più appropriata è la regressione pesata (wighted least-squares regression), che rende massima l’efficienza nella stima dei parametri della retta. Rappresenta il tentativo di

-  assegnare, ad ogni coppia di dati, la quantità appropriata di influenza che essa esercita nella determinazione del coefficiente angolare  e dell’intercetta  della retta.

 

Nella figura, si evidenzia con chiarezza che i valori  hanno misure  ripetute, caratterizzate da una precisione dell’informazione che non è costante. Nelle scienze analitiche, da  quelle chimiche a quelle cliniche,

- il livello di precisione della misura rilevata cambia al variare della sua concentrazione.

In questi casi, è utile ricorrere alla regressione pesata, che richiede calcoli più complessi di quelli fino ad ora presentati. Normalmente, essi sono effettuati con programmi informatici, per cui in questo paragrafo la presentazione è limitata alle nozioni generali.

 

Il concetto di base della weighted regression è

-  assegnare un peso  maggiore ai punti che hanno una precisione  maggiore.

 

Un modo per giungere a una soluzione è partire dalla relazione

 dove

-  è la varianza delle risposte  per la stessa dose o concentrazione .

 

Questi pesi iniziali possono essere standardizzati, in modo da ottenere un peso finale ,

- moltiplicandoli per il numero  di valori  

- e dividendo per la somma di tutti i pesi

 

Per una regressione pesata che passa per l’origine,

 quindi definita dalla retta

 

 la predizione inversa pesata è data da

 con

 dove

-  è il valore medio della risposta di  repliche

-   e  sono le coppie di dati  per il punto -esimo.

 

Assumendo che la retta di regressione passi per l’origine, la stima migliore del coefficiente angolare  è ottenuta nell’assunzione che l’ipotesi  = 0 sia corretta.

E’ ragionevole per molti dei casi nei quali si ricorre alla calibrazione, ma non sempre.

L’incertezza associata alla predizione inversa pesata, espressa come intervallo di confidenza, è stimata

 con

 dove

-  è il valore critico alla probabilità  (abitualmente = 0.05) bilaterale, con gdl  uguali a

-  è la deviazione standard pesata per il dato  per il punto  nella calibrazione,

-  è il numero di repliche e dei residui pesati,

-   è l’errore standard della calibrazione,

 calcolato come

 

Il vantaggio della regressione pesata è che

-  i pesi sono inversamente proporzionali alla varianza di ogni livello della variabile esplicativa.

E’ un concetto semplice, ma che ne rappresenta anche il limite maggiore. Infatti la teoria di questo metodo è fondata sull’assunzione che

-  i pesi sono conosciuti con precisione.

E’ una condizione che è realizzata solo raramente e pertanto vengono utilizzati i pesi del campione. Ma essi possono essere anche sensibilmente differenti da quelli reali, per cui sia l’analisi della regressione sia la sua interpretazione ne possono risultare fortemente influenzate.

Inoltre, come avviene per la varianza, i pesi calcolati sono fortemente influenzati dagli outlier. Ne deriva che il risultato di una regressione pesata può essere molto inferiore a quella di una regressione non pesata.