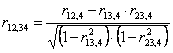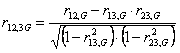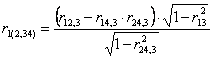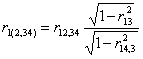CORRELAZIONE  E  COVARIANZA

 

 

18.10.   La correlazione parziale o netta di primo ordine E Di ordine superiore;  la correlazione semiparziale

 

Quando si analizzano le relazioni tra più variabili, la correlazione tra due di esse risente anche delle relazioni esistenti con le altre. Sovente, nella ricerca è richiesto di valutare l'associazione tra due variabili, eliminando l'influsso delle altre:

-   è la correlazione parziale o netta (partial correlation),

-   mentre quella discussa nei paragrafi precedenti è la correlazione semplice o totale.

 

Per esempio, nel caso in cui si intenda valutare le correlazioni tra 3 variabili come altezza, peso e circonferenza toracica, le relazioni esistenti tra circonferenza toracica ed altezza sono influenzate in modo rilevante da quelle esistenti tra ognuna di queste due con il peso. Nello stesso modo, la correlazione tra altezza e diametro del tronco di un albero risente della correlazione di entrambi con la sua età.

La correlazione parziale o netta è la stima della correlazione tra due variabili, dopo l'eliminazione degli effetti dovuti all'eventuale associazione con la terza (o il restante gruppo di k variabili).

Un metodo teoricamente possibile per valutare la correlazione netta tra due variabili sarebbe la misura della correlazione semplice o totale, mantenendo costante la terza variabile. Ma questa procedura presenta vari inconvenienti, facilmente identificabili:

-   la necessità di ripetere più volte i calcoli;

-   l’impossibilità di estendere e generalizzare le conclusioni, poiché per ogni valore della terza variabile si avrebbe una correlazione con un valore campionario differente;

-   un forte aumento della numerosità del campione e quindi sia dei costi che dei tempi richiesti dalla ricerca.

 

Nel suo testo già citato, (nella traduzione italiana) Fisher scriveva: “Grande parte dell’utilità dell’idea della correlazione risiede nella sua applicazione a gruppi con più di due variabili. In tali casi, in cui è nota la correlazione tra ciascuna coppia di tre variabili, se ne può eliminare una qualunque e trovar che in una popolazione scelta la correlazione delle altre due sarebbe da considerare come se la terza variabile fosse costante.

Quando le stime delle tre correlazioni sono ottenibili dalla stessa massa di dati, il processo di eliminazione fornirà una stima della correlazione parziale paragonabile in tutto e per tutto a una stima diretta”.

 

Nel linguaggio statistico, per misurare la correlazione parziale o netta tra due variabili si distinguono correlazioni di vari gradi od ordini, in rapporto al numero di variabili complessivamente utilizzate, ricordando che il concetto di correlazione riguarda la relazione esistente tra due.

- Quando si dispone solamente delle osservazioni relative a due variabili (come in precedenza),

la correlazione è detta di grado zero o di ordine zero;

- quando le variabili osservate sono tre, la correlazione tra due senza l'influenza della terza è detta

 correlazione di 1° grado o di 1° ordine;

con quattro variabili, eliminata l'influenza di due,

- la correlazione è di 2° grado o di 2° ordine;

con N variabili, eliminata l'influenza delle altre N-2,

- la correlazione tra due variabili è di grado od ordine (N-2)esimo.

 

Nel caso di tre variabili, quando sono stati calcolati i coefficienti di correlazione semplice o totale, il coefficiente di correlazione parziale o netta (scritta come r_12,3 e detta correlazione tra le variabili X₁ e X₂ al netto degli effetti della variabile X₃) è data da

 

con gdl  N-3, dove

-   è la correlazione parziale tra le variabili 1 e 2, a meno (o al netto) degli effetti della 3;

-   sono le correlazioni semplici tra le rispettive coppie di variabili.

 

Per la stima della correlazione netta, le condizioni di validità sono essenzialmente due:

-  le correlazioni di ordine zero devono essere lineari;

-  il numero N di osservazioni di ogni correlazione di ordine zero deve essere sempre superiore di alcune unità al numero delle variabili, poiché

 il numero di gdl della correlazione parziale con  k  variabili è uguale a  N-k.

 

ESEMPIO 1.  Si considerino i 18 laghi dell'Appennino tosco-emiliano, già utilizzati precedentemente, per ognuno dei quali è stata misurata

-   la conducibilità (X₁ ),

-   la concentrazione di Ione Calcio + Ione Magnesio (X₂ ),

-   la concentrazione di Solfati + Carbonati (X₃ ).

I valori sono riportati nella tabella successiva

 

 

 

Calcolare i tre coefficienti di correlazione semplice o totale. Successivamente, al fine di valutare con maggiore precisione la correlazione esistente tra queste variabili, stimare i tre coefficienti di correlazione parziale.

 

Risposta.  I tre coefficienti di correlazione semplice o totale (calcolati con un programma informatico) sono risultati:

r₁₂ = 0.9628

r₁₃ = 0,9704

r₂₃ = 0,9388

Poiché la tabella di valori di correlazione semplice

 con 16 df (N-2 = 18-2) e alla probabilità a = 0.001, riporta il valore 0,7484

 si deve concludere che i tre coefficienti di correlazione semplice sono tutti altamente significativi.

 

L’analisi  con la correlazione netta permette di valutare se questi valori di correlazione tra coppie di variabili sono rafforzati dalla comune correlazione con la terza, per cui le correlazioni reali tra coppie di variabili sono minori.

Applicando la precedente formula

le stime dei 3 coefficienti di correlazione parziale danno i risultati seguenti:

- r_12,3

r_12,3  =  =    =  0,623

 è uguale a 0,623;

 

- r_13,2

r_13,2  =    =  0,714

 è uguale a 0,714;

 

- r_23,1

r_23,1  =   = 0,069

 è uguale a 0,069.

 

I valori critici sono riportati nella solita tabella dei coefficienti di correlazione;

questi coefficienti di correlazione con  df 15 (N-k = 18-3)

-   alla probabilità a = 0.05 danno un valore di r uguale a 0,4821

-   mentre alla probabilità a = 0.01 è uguale a 0,6055

-   e alla probabilità a = 0.001 è 0,7247.

E’ semplice osservare che i 3 coefficienti netti calcolati risultano minori di quelli semplici; quindi è ovvio dedurre che la correlazione totale tra due variabili era aumentata dalla comune correlazione con la terza variabile.

 

In merito alla loro significatività, in modo più dettagliato,

-  il valore di r_12,3 risulta significativo con probabilità inferiore a 0.01

-  il valore di r_13,2 è significativo con probabilità inferiore a 0.001

-  il valore di r_23,1 non è significativo; anzi è molto distante dalla significatività e prossimo alla totale assenza di correlazione.

 

ESEMPIO 2. Come secondo caso e approfondimento delle potenzialità del metodo, è utile riportare l’esempio sviluppato da Fisher. Eliminazione dell’età in correlazioni organiche con fanciulli in fase di sviluppo. (In “Metodi statistici ad uso dei ricercatori, Torino 1948, Unione Tipografica Editrice Torinese (UTET), 326 p. traduzione di M Giorda, del testo Statistical Methods for Research Workers di R. A. Fisher 1945, nona edizione (la prima è del 1925) a pag. 174.)

Con i “dati di Munford e di Young, in un gruppo di fanciulli di differente età, si trovò che la correlazione fra statura in piedi e perimetro toracico era +0,836. Ci si potrebbe attendere che parte di questa associazione sia dovuta allo sviluppo generale in rapporto all’età crescente. Sarebbe quindi molto desiderabile, sotto vari aspetti, conoscere la correlazione tra le variabili in fanciulli d’una determinata età; ma nella fattispecie soltanto pochi fanciulli saranno esattamente della stessa età ed anche se compiliamo gruppi di età limitati a un anno, avremo in ciascun gruppo un numero molto inferiore al numero totale misurato. Al fine di utilizzare l’intero materiale, dobbiamo limitarci alla conoscenza delle correlazioni tra statura in piedi e perimetro toracico ed età.”

Spiegando tutti i passaggi, dai valori di

-   statura in piedi (1)  e perimetro toracico (2) si ottiene r₁₂ = +0,836

-   statura in piedi (1)  e età (3) si ottiene r₁₃ = +0,714

-   perimetro toracico (2) e età (3) si ottiene r₂₃ = +0,836

 

Da essi ricava r_12,3

 

 

“Inserendo i termini numerici nella formula data, otteniamo r_12,3 =  0,668, indicante che, quando l’età è eliminata, la correlazione, quantunque ancora considerevole, è stata notevolmente ridotta. Il valore medio stabilito dagli autori summenzionati per le correlazioni trovate raggruppando i fanciulli per anni è 0,653, un valore, cioè, non molto differente.”

 

Nell’analisi dei coefficiente di correlazione parziale o netta si possono realizzare due situazioni:

-   se il valore parziale è maggiore di quello semplice o addirittura diventa significativo, si deve dedurre che l’altro fattore nasconde la correlazione che effettivamente esiste;

-   se il coefficiente parziale è minore di quello semplice o addirittura perde la significatività, si può dedurre che la terza variabile considerata è fortemente correlata con entrambe e le fa variare congiuntamente, senza che tra esse esista una relazione diretta.

 

La significatività della regressione risente in modo marcato di due fattori:

-  il numero di osservazioni

-  il campo di variazione di X₁ e X₂.

L’importanza del primo fattore è evidenziata dalla semplice lettura della tabella dei valori critici, che diminuiscono in modo rilevante all’aumentare del numero di gradi di libertà, come già sottolineato per la regressione lineare semplice.

Per il secondo fattore, si può osservare che

-   quando i valori delle due variabili hanno un intervallo molto limitato, il coefficiente di correlazione ha un valore assoluto molto basso, difficilmente significativo;

-   al contrario, quando anche solo una variabile ha un intervallo di variazione molto ampio, il coefficiente di correlazione è molto alto.

 

Per la corretta programmazione di un esperimento, è quindi conveniente

-   raccogliere in precedenza informazioni sulla loro variabilità e

-   impostare la raccolta dei dati in modo che essa sia grande.

 

Inoltre, poiché l’interpretazione della correlazione tra due variabili è fortemente influenzata

-   sia dal numero di dati,

-   sia dal campo di variazione,

è difficile confrontare la significatività di due coefficienti di correlazione con dati raccolti in condizioni diverse.

Con metodi molto simili alla correlazione parziale di primo ordine, gli stessi principi possono essere estesi a 4 o più variabili, con la correlazione parziale di secondo ordine e a quella di ordine superiore.

Prendendo in considerazione 4 variabili (X₁, X₂, X₃, X₄),

ognuna con lo stesso numero N di osservazioni,

si devono calcolare i 6 coefficienti i correlazione semplice o totale (r₁₂, r₁₃, r₁₄, r₂₃, r₂₄, r₃₄).

 

La correlazione parziale di secondo ordine tra due di queste variabili X₁ e X₂ , mantenendo costanti le altre due X₃ e X₄ (scritta  ),

può essere calcolata con la formula

che utilizza tre correlazioni parziali di primo ordine ().

 

Con più di 4 variabili (X₁, X₂, X₃, X₄, …, X_n), la formula generale, per calcolare la correlazione parziale tra la variabile X₁ e X₂ con le variabili X₃ e X_G (il gruppo di tutte le altre) mantenute costanti, diventa

 

Per i calcoli è necessario utilizzare un programma informatico, dato l’alto numero di operazioni da effettuare e quindi l’elevata probabilità di commettere errori.

 

ESEMPIO 3. (Continua l’esempio e la trattazione di Fisher)

“In modo simile, possono successivamente essere eliminate due o più variabili; così con quattro variabili, possiamo prima eliminare la variabile 4, applicando tre volte la formula per trovare r_12,4, r_13,4 e r_23,4. Quindi tornando ad applicare la medesima formula a questi tre nuovi valori, si ottiene

Il lavoro aumenta rapidamente col numero delle variabili da eliminare. Per eliminare s variabili, il numero delle operazioni necessario, ciascuna variabile importando l’applicazione della stessa formula, è

Per valori di s da 1 a 6, occorrono perciò 1,  4,  10,  20,  35,  56 operazioni.

Gran parte di questa fatica può essere risparmiata usando le tavole di  quali quelle pubblicate da J. R. Miner.

 

Come le variabili indipendenti nella regressione, le variabili eliminate nell’analisi della correlazione non comparvero distribuite, anche approssimativamente, in distribuzioni normali. Del pari e questo è assai di frequente trascurato, errori casuali in esse introducono errori sistematici nei risultati. Per esempio, se la correlazione parziale delle variabili (1) e (2) fosse realmente zero, dimodochè r₁₂ fosse uguale a r₁₃×r₂₃, errori casuali nella misura o nella valutazione della variabile (3)  tenderebbero a ridurre numericamente r₁₂ e r₂₃ in modo da rendere il loro prodotto numericamente minore di r₁₂. Un’apparente correlazione parziale fra le prime due variabili sarà, perciò, prodotta da errori casuali nella terza.

 

Mentre le correlazione parziale  valuta gli effetti tra due variabili (X₁ e X₂) dopo che entrambe sono state aggiustate per la regressione con la terza variabile (X₃), per cui essa è la correlazione tra due variabili aggiustate (X_1,3 e X_2,3),

la correlazione semiparziale (semipartial or part correlation)  

-   valuta la correlazione tra la variabile X₁ e la variabile X₂,

-   dopo che solo la X₂ è stata aggiustata per la variabile X₃ (indicata con X_2,3).

La correlazione semi-parziale è quindi la correlazione tra una variabile non aggiustata (X₁) ed una seconda variabile aggiustata per la terza (X_(2,3))

ed è calcolata con

 

Un esempio di correlazione parziale riportato nei testi è la correlazione tra la perdita di peso in un gruppo N pazienti e il tempo che ognuno di essi dedica alla ginnastica, aggiustato per il consumo di calorie che l’esercizio, più o meno faticoso, comporta. Nella ricerca ambientale può essere il caso di salinità, ossigeno e temperatura

Con 3 variabili (X₁, X₂, X₃) sono teoricamente possibili 6 correlazioni parziali: oltre alla precedente , si hanno

 

 

ed in modo analogo le altre tre  , ,

anche se spesso hanno reale significato ecologico od ambientale solo una o due di esse. Non è quindi necessario calcolarle tutte, ma è bene limitare l’analisi a quelle che  possono essere interpretate.

Anche nella correlazione semiparziale, una variabile può essere aggiustata per un numero più alto di variabili, non solo per una terza.

 

La correlazione semiparziale di secondo ordine  può essere stimata

-   sia partendo dalle correlazioni parziali di primo ordine con

 

-   sia partendo da quella di secondo ordine con

 

Le correlazioni parziali e semi-parziali hanno la loro applicazione principale nello studio delle inter-relazioni lineari che esistono fra tre o più variabili. E’ un concetto di estrema importanza nella teoria della regressione multipla, che è alla base della statistica multivariata.

Come dimostrato nella esposizione, Fisher attribuiva molta importanza a questi metodi di correlazione parziale, pure avvisando degli effetti determinati dagli errori casuali. Nella statistica moderna, come suggerito da vari autori, si preferisce ricorre alla regressione multipla.