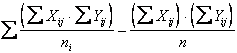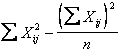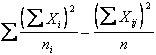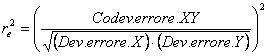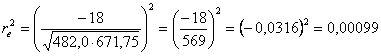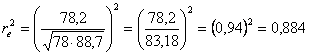|
CORRELAZIONE E COVARIANZA
18.12. ANALISI DELLA COVARIANZA PER K GRUPPI (ANCOVA) E RIDUZIONE PROPORZIONALE DELLA VARIANZA D’ERRORE
Con k gruppi, il caso più semplice è quello di un disegno sperimentale completamente randomizzato. Ricorrendo alla simbologia consueta, mentre nell’analisi della varianza a un criterio di classificazione il modello è Yij = m + ai + eij nell’analisi della covarianza diviene Yij = m + ai + b(xij -
Nell’analisi della covarianza è possibile utilizzare una variabile concomitante X, chiamata covariata, che spiega parte della variabilità della variabile dipendente Y. Consente un calcolo più preciso degli effetti dei trattamenti, riducendo la variabilità casuale, cioè non controllata. Per esempio, si supponga di voler stimare l’effetto di tre tossici (ai) sul peso (Yi) delle cavie. L’analisi della varianza ad un solo criterio di classificazione richiede che si formino tre gruppi, inizialmente identici per caratteristiche degli individui; dopo un periodo di somministrazione del principio attivo, le differenze tra i pesi medi dei tre gruppi permettono di valutare l’effetto dei tossici sulla crescita ponderale delle cavie. Ma avere tre gruppi di cavie con le stesse dimensioni iniziali spesso è difficile, soprattutto se l’esperimento non avviene in laboratorio ma in natura, con animali catturati.
Un altro caso
sovente citato nei testi di statistica applicata è il confronto tra il peso (Yi)
di organi di animali sottoposti a trattamenti (ai) diversi, in cui
il peso dell’organo dipende sia dall’effetto del trattamento che dalle
dimensioni (Xi) dell’animale. E’ possibile eliminare dal peso
dell’organo quella quantità che dipende delle dimensioni dell’animale [b(xij - Si parla di analisi after the fact, che permette di valutare quale sarebbe stato il risultato, se la variabile concomitante X fosse stata costante per tutti i gruppi.
Attualmente, poiché i calcoli vengono eseguiti dai programmi informatici, è diventato importante capire più che eseguire. Il test richiede alcuni passaggi logici, che possono essere riassunti in 5 punti.
1 - Si applica l’analisi della varianza alle Y, per verificare l’ipotesi nulla H0: m1 = m2 = m3 =... = mk se le medie delle popolazioni dalle quali sono estratti i k campioni a confronto sono uguali, con ipotesi alternativa H1 che non tutte le m sono uguali.
Con le formule abbreviate abituali si calcolano: - la devianza totale delle Y
- la devianza tra trattamenti delle Y
- e, per differenza, la devianza d’errore delle Y Dev. Y totale - Dev. Y tra tratt. con df n - k dove - - -
Stimata la varianza tra trattamenti e la varianza d’errore, si perviene al test F F(k-1,
n-k) =
che raramente risulta significativo, se l’effetto della regressione di Y su X è elevato.
2 - Per correggere i dati calcolati, si valuta l’effetto della regressione ricordando che è la sua devianza è stimata dal rapporto
A questo scopo si devono calcolare: - la codevianza XY totale
- la codevianza XY tra trattamenti
- e, per differenza, la codevianza XY d’errore Cod. XY totale - Cod. XY tra trattamenti
(A questo proposito, è importante ricordare che le Codevianze possono risultare sia positive che negative. Per esempio, con una Codevianza XY totale positiva si può ottenere anche una Codevianza XY tra trattamenti che risulti negativa; di conseguenza, la Codevianza XY d’errore può risultare maggiore di quella totale.)
3 - Sempre per stimare l’effetto della regressione, è preliminare effettuare il calcolo delle devianze delle X, con le stesse modalità seguite per la Y: - la devianza totale delle X
- la devianza tra trattamenti delle X
- e, per differenza, la devianza d’errore delle X Dev. X totale - Dev. X tra tratt.
4 - Con i valori calcolati al punto 2 e al punto 3, si stimano le Devianze dovute alla regressione del coefficiente b comune; servono solo la devianza totale e quella d’errore, ottenute da: - devianza totale dovuta alla regressione
- e la devianza d’errore dovuta alla regressione
- la devianza tra trattamenti dovuta alla regressione non serve, per il motivo che spiegato nel passaggio successivo
5 - E’ così possibile ottenere le devianze delle Y ridotte o devianze dovute alle deviazioni della regressione, sottraendo alla devianza totale e alla devianza d’errore delle Y, calcolate al punto 1, quelle rispettive calcolate al punto 4. Si stimano: - la devianza totale delle Y ridotte Dev. Y totale - Dev. Y totale della regressione con df (n - 1) - 1 (In questa operazione, che trasferisce il confronto dei singoli valori della Y dalla media generale alla retta di regressione comune, si perde un altro df)
- e la devianza d’errore delle Y ridotte Dev. Y d’errore - Dev. Y d’errore della regressione con df (n - k) - 1 (Come in precedenza, rispetto alla devianza d’errore delle Y, calcolata al punto 1, ha 1 df in meno)
La devianza tra trattamenti delle Y ridotte è ottenuta per differenza tra queste due immediatamente precedenti: Dev. delle Y ridotte totale - Dev. delle Y ridotte d’errore con df k - 1 che mantiene i suoi df = k - 1. Questa stima della devianza tra trattamenti è ottenuta per differenza e non più per semplice sottrazione della devianza tra trattamenti che poteva essere calcolata al punto 4, in modo analogo, da quella tra trattamenti calcolata al punto 1 perché ne avrebbe stimato solamente una parte: infatti essa deve comprendere - sia gli scostamenti delle medie di gruppo intorno a una retta di regressione calcolata per la variabilità tra i gruppi, cioè interpolate per le medie dei gruppi, - sia la differenza tra le pendenze delle rette di regressione parallele, calcolate entro gruppi, con la pendenza della retta di regressione interpolata tra le medie di gruppo.
6 - Calcolate la varianza tra trattamenti e la varianza d’errore sulle Y ridotte, il test F, che considera l’effetto della regressione sui valori delle Y, è dato dal loro rapporto
F (k-1, n-k-1)
=
ESEMPIO 1. A tre gruppi di cavie sono state somministrate tre sostanze tossiche (A, B, C) che, alterando il metabolismo, determinano un forte aumento ponderale. Poiché sono stati utilizzati animali di dimensioni diverse, per valutare correttamente gli effetti sul peso (Y) deve essere considerata anche la lunghezza (X) delle cavie.
TRATTAMENTI
(Il metodo non richiede che i tre gruppi abbiano lo stesso numero di osservazioni, essendo del tutto analogo all’analisi della varianza a un criterio di classificazione. Per facilitare il calcolo manuale, pesi ed altezze sono stati riportati in valori trasformati, che non modificano i risultati; inoltre, sempre per facilitare i calcoli, sono state scelti campioni molto piccoli, spesso insufficienti per un esperimento reale).
Con questi dati, effettuare l’analisi della varianza e della covarianza, per valutare compiutamente l’effetto delle tre sostanze sul peso finale delle cavie.
Risposta. Prima di procedere alle analisi, è sempre di elevata utilità una rappresentazione grafica dei dati e delle medie a confronto.
Il diagramma di dispersione dei 3 gruppi mostra che le differenze tra le tre medie dei valori campionari di Y sono ridotte e che la regressione lineare tra lunghezza X e peso Y per ogni gruppo è evidente, con coefficienti angolari simili. Per l’interpretazione dei risultati e per i calcoli successivi con le formule abbreviate, è utile determinare preliminarmente le seguenti serie di somme e medie:
Somma XA = 112 Somma XB = 90 Somma XC = 94 Somma X = 296 Somma YA = 77 Somma YB = 105 Somma YC = 85 Somma Y = 267 nA= 5 nB = 6 nC = 5 n = 16
media XA = 22,40 media XB = 15,00 media XC = 18,80 media X = 18,50 media YA = 15,40 media YB = 17,50 media YC = 17,00 media Y = 16,6875
Somma X2A = 2532 Somma X2B = 1396 Somma X2C = 1776 Somma X2 = 5704 Somma Y2A = 1201 Somma X2B = 1901 Somma X2C = 1445 Somma X2 = 4557
Somma XYA = 1743 Somma XYB = 1628 Somma XYC = 1605 Somma XY = 4976
Seguendo lo stesso schema precedentemente descritto, i calcoli da effettuare possono essere raggruppati in 5 fasi.
1 - Per l’analisi della varianza ad 1 criterio di classificazione sui valori di Y (peso), si devono stimare i valori di - la devianza Y totale 4557 -
che risulta uguale a 101,56 ed ha 15 df, - la devianza Y tra trattamenti
che è uguale a 12,74 ed ha 2 df - la devianza Y d’errore 101,44 - 12,74 = 88,7 che è uguale a 88,7 ed ha 13 df (15-2). I risultati possono essere presentati in una tabella
dalla quale risulta evidente che il valore di F è inferiore a 1; pertanto, le differenze tra le medie campionarie non sono assolutamente significative.
2 - Per tenere in considerazione l’effetto della regressione, occorre calcolare le codevianze tra X e Y; quindi: - la codevianza XY totale 4976 - che risulta uguale a 36,5 - la codevianza XY tra trattamenti
che ha un valore negativo (- 41,7) - la codevianza XY d’errore 36,5 - (-41,7) = 78,2 che risulta maggiore di quella totale (78,2).
3 - Per procedere alle stime richieste è necessario calcolare anche le devianze di X: - la devianza X totale
che è uguale a 228 - la devianza X tra trattamenti
risulta uguale a 150, - la devianza X d’errore 228 - 150 = 78 uguale a 78.
4 - Le devianze dovute alla regressione b comune, necessarie alla stima della Y ridotte, sono: - la devianza totale della regressione
che risulta uguale a 5,84, - la devianza d’errore della regressione
che risulta uguale a 78,4.
5 - In conclusione, le devianze dovute alle deviazioni dalla regressione o devianze delle Y corrette sono: - la devianza totale delle Y corrette 101,44 - 5,84 = 95,6 uguale a 95,6 con 14 df a causa della perdita di un altro df dovuto alla correzione per la regressione (16 - 1 - 1), - la devianza d’errore delle Y corrette 88,7 - 78,4 = 10,3 uguale a 10,3 con df 12 (anch’esso perde un altro df, poiché diventa l’errore intorno alla retta), e, per differenza, - la devianza tra trattamenti delle Y corrette 95,6 - 10,3 = 85,3 che risulta uguale a 85,3 con 2 df.
6 - Con questi ultimi dati, è possibile applicare l’analisi della varianza dei valori di Y che considerano l’effetto di regressione sulla X
e permettono un test F F(2,12)
= che risulta altamente significativo.
ESEMPIO 2. Riprendendo i dati presentati da William L. Hays nel suo testo del 1994 (Statistics, 5th ed. Holt, Rinehart and Winston, Fort Worth, Texas), si assuma di confrontare cinque differenti modalità (A, B, C, D, E) di trasformazione farmacologica di un prodotto naturale di base (X), dal quale viene derivato il prodotto industriale finito (Y). La tabella riporta la concentrazione della sostanza nel prodotto da trasformare (X) e in quello trasformato (Y)
Si vuole valutare
se la produzione media del prodotto finito (
Risposta. Presentando solo i calcoli da effettuare, i passaggi possono essere schematizzati in 4 punti.
1) Come nell’analisi della varianza a un criterio di classificazione o completamente randomizzata, si calcolano le devianze e i loro gdl, ovviamente per le Y. Oltre ai totali di gruppo riportati nella tabella, dapprima si stimano
Con le solite formule delle devianze si ricavano:
- Dev. Y Totale
- Dev. Y Tra
- Dev. Y errore 2.670,55 – 1.988,80 = 671,75 con gdl = 15
2) Con le stesse modalità si calcolano le devianze delle X, poiché servono successivamente per correggere le devianze delle Y appena stimate. Oltre ai totali di gruppo riportati nella tabella, si eseguono le somme
e da essi si ricavano:
- Dev. X Totale
- Dev. X Tra
- Dev. X errore 1.577,8 – 1.095,8 = 482,0
3) Per lo stesso scopo si stimano le codevianze; oltre ai totali di gruppo riportati nella tabella, si stimano
e da essi si ricavano:
- Codev. XY Totale
- Codev. XY Tra
- Codev. XY errore 1.3321,30 – 1.349,30 = -18,0 (Osservare che con le codevianze, che possono essere negative, si mantiene la proprietà additiva; di conseguenza, quella tra trattamenti può essere maggiore di quella totale e quindi la codevianza d’errore risultare negativa)
4) Infine si ricavano le devianze delle Y aggiustate
Dev. Y aggiustate =
ottenendo - Dev. Y aggiustate Totale (perde un altro gdl)
- Dev. Y aggiustate errore (perde anch’esso un altro gdl)
Da queste due, per differenza, si stima - Dev. Y aggiustate Tra 1.547,24 – 671, 08 = 876, 16 con gdl = 4
E’ utile riportare questi dati conclusivi delle devianze aggiustate nella solita tabella dell’ANOVA
In essa sono stati aggiunti il valore di F
e la probabilità P < 0.025 che permette di rifiutare l’ipotesi nulla. Infatti con DF 4 e 14 i valori critici riportati nelle tabelle sono - F = 3,89 alla probabilità a = 0.025 - F = 5,04 alla probabilità a = 0.01
Allo scopo di valutare il vantaggio apportato dall’analisi della
covarianza alla significatività delle differenze tra le medie della Y è utile
fornire la stima della riduzione proporzionale della varianza d’errore
Nell’ultimo esempio, con i dati Codev. Errore di XY = -18 Dev. Errore della X = 482,0 Dev. Errore della Y = 671,75 si ottiene
che la correzione relativa è stata minore di 0.001, quindi totalmente trascurabile.
Nell’esempio 1, con Codev. Errore di XY = 78,2 Dev. Errore della X = 78 Dev. Errore della Y = 88,7 si ottiene
una correzione relativa che è superiore all’88 per cento. E’ molto importante, tale da rendere significativo il test F sull’uguaglianza delle medie di Y, mentre prima non lo era.
A conclusione della dimostrazione sperimentale del metodo, è utile rivedere i concetti di base della regressione e le sue condizioni di validità. Il caso presentato è il modello dell’analisi della Covarianza per un solo fattore (Single-Factor Covariance Model) del tutto simile all’analisi della varianza ad effetti fissi. Con una simbologia leggermente modificata da quella sempre utilizzata, al solo scopo di rendere più facilmente leggibile la figura successiva, questo modello può essere scritto come
dove - -
- Il valore di Gli errori (
L’analisi della covarianza ha come ipotesi nulla H0: contro l’ipotesi alternativa H1: non
tutte le
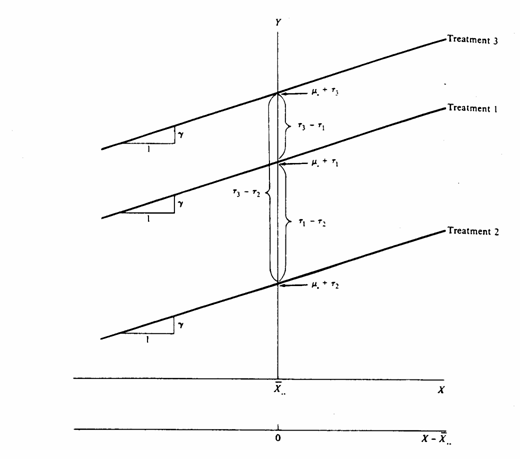
In una analisi della covarianza con 3 trattamenti, i vari concetti possono essere rappresentati graficamente come nella figura prossima:
In essa sono evidenziati gli aspetti più importanti dell’analisi della covarianza.
A) I valori delle
Y nei tre trattamenti sono rappresentate lungo altrettante rette, tra loro
parallele, che esprimono la relazione con la variabile concomitante X. Vale a
dire, riprendendo l’esempio sulla relazione tra capacità respiratoria espressa
in litri (
B) I vari gruppi
a confronto possono avere medie delle X differenti (
Le condizioni di validità sono cinque: 1) la normalità degli errori, 2) l’uguaglianza della varianza per i vari trattamenti, 3) l’uguaglianza del coefficiente angolare delle rette di regressione dei vari trattamenti, 4) la relazione di regressione tra la variabile X e la variabile Y deve essere lineare, 5) gli errori non devono essere correlati.
La terza
assunzione, quella che tutti i trattamenti devono avere lo stesso
coefficiente angolare (nel testo sempre indicato con Se i coefficienti angolari sono differenti, nell’analisi statistica occorre separare i trattamenti. Per ottenere questo risultato, il metodo più semplice è quello illustrato per il caso di due campioni, nel paragrafo precedente.
Con un approccio differente dai metodi esposti, l’analisi della covarianza può essere affrontata anche con il calcolo matriciale. E’ un argomento che rientra nella statistica multivariata, per la quale è necessaria una impostazione differente e più complessa di quella qui esposta. Ad essa si rimanda per approfondimenti ulteriori.
L’analisi della covarianza ha avuto ampi sviluppi, in due direzioni diverse. - Da una parte, in analogia con l’analisi della varianza, permette di considerare contemporaneamente vari fattori e le loro interazioni, in riferimento a una sola covariata. Se l’analisi è limitata a due sole variabili, con la consueta simbologia il modello additivo è
Yijk = m + ai gj + agij + b(Xijk -
- Dall’altra, con la covarianza multipla si possono seguire più covariate (X1 , X2 ,…, Xn). Il modello più semplice, due covariate in una analisi della varianza ad 1 solo criterio, è Yijk = m + ai + b1(X1ij -
Dalla loro combinazione, più variabili e più covariate, si ottengono modelli additivi che appaiono molto complessi. Superati con l’informatica i problemi di calcolo, attualmente i limiti alla complessità del disegno sperimentale sono posti solamente dall’interpretazione dei risultati, particolarmente difficile nel caso di più interazioni.
Per la trattazione dell’analisi della covarianza a disegni complessi, più variabili e più covariate con eventuale interazione, si invia a testi specifici.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
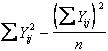 con df n
- 1
con df n
- 1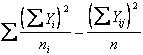 con df k
- 1
con df k
- 1