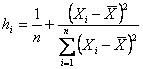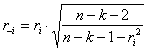CORRELAZIONE  E  COVARIANZA

 

 

18.15.    HAT VALUE O LEVERAGE, STUDENTIZED DELETED RESIDUALS.

 

 

La ricerca degli outlier nella regressione lineare è strettamente associata al problema più ampio della validità stessa della regressione, che è fondata su tre assunzioni:

1 – la media della popolazione della variabile dipendente, per l’intervallo di valori della variabile indipendente che è stato campionato, deve cambiare in modo lineare in rapporto ai valori della variabile indipendente;

2 – per ogni valore della variabile indipendente, i valori possibili della variabile dipendente devono essere distribuiti normalmente;

 3 – la deviazione standard della variabile dipendente intorno alla sua media (la retta), per un dato intervallo di valori della variabile indipendente, deve essere uguale per tutti i valori della variabile indipendente.

 

La presenza anche di un solo outlier nelle Y, per un certo valore della X, modificando

-  la media, che in questo caso è la retta (assunto 1),

-  la forma della distribuzione (assunto 2),

-  la deviazione standard (assunto 3),

 rende irrealizzate queste condizioni di validità.

Anche quando non si intende analizzare se è presente almeno un outlier, la distribuzione effettiva dei dati può determinare una o più di queste condizioni. Ne consegue che, per affermare statisticamente la validità di una retta, sarebbe importante applicare sempre alcune delle tecniche diagnostiche della regressione (regression diagnostics), per valutare i suoi residui.

 

Nel testo

-  di R. L. Mason, R.F: Gunst e J. L. Hess del 1989 Statistical Design and Analysis of Experiments (edito da John Wiley and Sons, New York, pp. 510-257)

- e in quello più recente di Stanton A. Glanz e Bryan K. Slinker del 2001 Primer of applied regression and analysis of variance (2^nd ed. Mc Graw-Hill, Inc., New York, 27 + 949),

 per citarne solamente due, tra quelli che affrontano questi argomenti, sono riportati vari metodi per una impostazione più generale e approfondita dell’analisi dei residui, in grado di assicurare la validità dell’analisi della regressione e della correlazione.

 

Glanz e Slinker, con esempi spesso divertenti, sviluppano una serie di applicazioni dei vari test di diagnostica della regressione, utilizzando dati totalmente inventati. Sono le misure di alcuni marziani, dei quali si vuole conoscere le caratteristiche fondamentali, attraverso l’analisi statistica. La pratica di avvalersi di dati non reali, in esercizi e in dimostrazioni di statistica applicata, è criticata da molti studiosi, in quanto può condurre a problemi e situazioni irreali. E’ l’opposto degli scopi specifici della disciplina. Ma in questo caso, data la competenza degli autori e nel contesto di tanti dati sperimentali, servono per illustrare con semplicità e rapidità una casistica numerosa e complessa di situazioni reali.

 

Di 11 marziani è stata misura la lunghezza del piede (in cm) e il quoziente d’intelligenza (in zorp)

 

 

 

E’ indicato come ESEMPIO A.

 

Non è noto se esista una relazione di causa-effetto tra le due variabili.

Tuttavia, come metodo esplorativo, è applicata l’analisi della regressione lineare semplice e viene calcolato il coefficiente di correlazione  (la cui significatività, ovviamente, è identica a quella del coefficiente angolare ).

Assumendo

-  come variabile indipendente (X) la lunghezza del piede

-  e come variabile dipendente (Y) il quoziente d’intelligenza,

 il programma informatico fornisce i seguenti risultati:

 

 

CAMPIONE A

The regression equation is:    = 3,00      = 0,500

 

Predictor     Coeff.     St.dev.     t-ratio     P

            3,000       1,125        2,67      0,026

           0,5001      0,1179        4,24      0,002

 

  s = 1,237      Rsq= 0,667      Rsq(adj)=0,629      r = 0,816

 

Analysis of variance

SOURCE       DF        SS        MS        F        P

Regression    1      27,510    27,510    17,99     0,002

Error         9      13,763     1,529

Total        10      41,273

 

 

Come evidenzia anche il diagramma di dispersione riportato nella pagina precedente (grafico A, in alto a sinistra),

-  la retta di regressione  è

- il coefficiente di correlazione è

- la linearità e la correlazione sono significative (con t = 4,24  o  F = 17,99  e  P = 0,002);

-  è significativamente differente da zero anche l’intercetta  (t = 2,67   e   P = 0.026).

 

Le altre tre figure (B, C, D) sono state costruite da Glanz e Slinker in modo tale che i dati, non riportati, forniscono le seguenti tre analisi della regressione:

 

 

CAMPIONE B

The regression equation is:    = 3,00      = 0,500

 

Predictor     Coeff.     St.dev.     t-ratio     P

            3,001       1,125        2,67      0,026

           0,5000      0,1180        4,24      0,002

 

  s=1,237      Rsq=0,666      Rsq(adj)=0,629      r=0,816

 

Analysis of variance

SOURCE       DF        SS        MS        F        P

Regression    1      27,500    27,500    17,97     0,002

Error         9      13,776     1,531

Total        10      41,276

 

 

CAMPIONE C

The regression equation is:    = 3,00      = 0,500

 

Predictor     Coeff.     St.dev.     t-ratio     P

            3,002       1,124        2,67      0,026

           0,4997      0,1179        4,24      0,002

 

  s=1,236      Rsq=0,666      Rsq(adj)=0,629      r=0,816

 

Analysis of variance

SOURCE       DF        SS        MS        F        P

Regression    1      27,470    27,470    17,97     0,002

Error         9      13,756     1,528

Total        10      41,226

 

CAMPIONE D

The regression equation is:    = 3,00      = 0,50

 

Predictor     Coeff.     St.dev.     t-ratio     P

            3,002       1,124        2,67      0,026

           0,4999      0,1178        4,24      0,002

 

  s=1,236      Rsq=0,667      Rsq(adj)=0,630      r=0,816

 

Analysis of variance

SOURCE       DF        SS        MS        F        P

Regression    1      27,490    27,490    18,00     0,002

Error         9      13,742     1,527

Total        10      41,232

 

 

Dalla lettura di queste tre tabelle, risulta con evidenza che i dati con i quali sono stati costruiti i tre grafici (B, C, D) hanno in comune con il grafico A

-  la stessa retta  di regressione:

-  lo stesso coefficiente di correlazione:

- lo stesso errore standard:  

Le piccole differenze nei test di significatività sono trascurabili.

 

Ma i quattro diagrammi di dispersione risultano visivamente molto differenti. Effettivamente hanno caratteristiche diverse, che è successivamente saranno quantificate in indici.

 

-    La figura A (in alto, a sinistra) rappresenta una situazione corretta, in cui sono rispettate le tre condizioni di validità e nella quale pertanto non sono presenti outlier.

 

-    La figura B (in alto, a destra) riproduce una situazione non corretta, in cui non sono rispettate tutte le condizioni di validità, ma nella quale non sono presenti outlier. Infatti la collocazione dei punti lungo la retta indica che la regressione esiste, ma che essa non è lineare. E’ un esempio classico di model misspecification, di scelta errata del modello di regressione.

 

-    La figura C (in basso, a sinistra) mostra una situazione non corretta, in cui non sono rispettate tutte le condizioni di validità e nella quale è presente un outlier, con un leggero swamping effect. Poiché la retta è fondata sul principio dei minimi quadrati, il valore anomalo ha un peso determinante sul coefficiente di regressione , attirandolo verso se. Questa capacità di attrazione di un punto è tanto maggiore, quanto più grande è la distanza del dato dal baricentro della distribuzione.

 

-   La figura D (in basso, a destra) rappresenta un’altra situazione non corretta, nella quale non sono rispettate tutte le condizioni di validità; soprattutto è presente un outlier, molto distante dagli altri e quindi con un peso sproporzionato sui coefficienti di regressione  e di correlazione .

 In termini tecnici, si dice che

-  è un leverage point o hat value

-  che ha un importante swamping effect.

Vale a dire che, come visibile nel diagramma di dispersione, è collocato in una posizione dove ha una forte capacità di sommergere l’informazione data da tutte le altre coppie di dati.

 

La retta e la correlazione di questa figura D non sarebbero significativi, senza la presenza di quel dato anomalo. Se il dato anomalo è un errore, è doveroso eliminarlo. Ma anche se è corretto, occorre molta cautela per poterlo utilizzare nel calcolo della regressione e della correlazione. Secondo Glanz e Slinker: Even if the point is valid, you should be extremely cautions when using the information in this figure to draw conclusions…. Such conclusions are essentially based on the value of a single point. It is essentials to collect more data … before drawing any conclusions.

 

Il problema statistico è come arrivare a conclusioni sulla validità delle analisi non sulla base di descrizioni qualitative, ma attraverso metodologie statistiche condivise che quantificano le diverse caratteristiche. In modo più dettagliato, a pag. 118 sempre Glanz e Slinker scrivono: These graphical differences are also quantitavely reflected in the value of regression diagnostics associated with the individual data points. These differences are the key to indentifying problems with the regression model or errors in the data. The fact we can fit a linear regression equation to a set of data - even if it yields a reasonably high and statistically significant correlation coefficient and small error of the estimate – does not ensure that the fit is appropriate or reasonable.

 

Come nel paragrafo precedente,

- le informazioni fondamentali sulla validità della regressione e della correlazione

- sono basati sui residui , detti anche raw residuals, per distinguerli più nettamente dagli altri residuals, diversamente aggettivati, che derivano da questi per elaborazioni successive.

L’analisi della normalità della distribuzione dei residui grezzi (raw residuals), dei residui studentizzati o di quelli standardizzati può essere effettuata con le tecniche illustrate per la statistica univariata.

 

Quindi, si rimanda ad esse. Anche su questi dati è utile

-   costruire il grafico dei residui,

-  applicare a essi il test di Tukey con il metodo Box-and-Wiskers,

-  calcolare e rappresentare graficamente i residui studentizzati, alla ricerca degli outlier.

 

Ma sono possibili e vantaggiose anche altri analisi, sebbene non esauriscano l’elenco:

-  stimare il leverage o hat value di ogni punto, che valutata l’influenza potenziale sulla regressione;

-  calcolare gli Studentized deleted residuals o externally Studentized residuals;

-  calcolare la distanza di Cook (Cook’s distance), che valuta l’influenza effettiva o reale (actual influence) di ogni punto sui risultati della regressione; è chiamata distanza ma è una misura d’influenza del dato sul risultato complessivo della regressione.

 

Il leverage o hat value è un termine usato nell’analisi della regressione multipla, per definire il peso che le singole osservazioni hanno sul valore della regressione. Sono di particolare interesse i dati con un valore estremo, in una o più variabili indipendenti. Per il principio dei minimi quadrati, la retta è forzata a passare vicino a quei punti, che pertanto hanno una grande capacità di attrarre verso di loro la retta e quindi di determinare residui piccoli.

Nel caso della regressione lineare semplice, quindi con una sola variabile indipendente, il leverage  del punto ,  è stimato con

 

Questo numero, che deve essere calcolato per ogni punto,

-   varia da 0 a 1,

-  è determinato dalla distanza del valore della variabile X dalla sua media

-   rapportato alla devianza totale della X.

Nell’esempio A, dove    = 9,0    e    = 110

- per il punto del marziano I  con X = 10  e  Y = 8,04

 il leverage

 

 è piccolo (uguale a 0,1000) poiché il suo valore di X è vicino alla media;

-   per il punto del marziano VIII  con X = 4  e  Y = 4,26

 il leverage

 

 è maggiore (uguale a 0,3182) poiché il suo valore di X è più lontano dalla media.

Il leverage è definito come

- una influenza potenziale del punto sulla regressione e correlazione, determinato dalla distanza del valore  dalla sua media .

 

Con i dati dell’esempio A, si osserva appunto che

-  il valore minimo di leverage è quello del marziano IV, poiché il suo valore della variabile X coincide con la media,

-  mentre è massimo per i marziani VI e VIII, che sono agli estremi per la variabile X

 

 

 

 

Idealmente, per una buona retta di regressione,

-  tutti i punti dovrebbero avere la stessa influenza sui parametri della retta di regressione;

- pertanto i valori di leverage dei punti campionati dovrebbero essere uguali e piccoli.

Nella regressione multipla il valore medio di leverage è 

 dove  è il numero di variabili indipendenti

Nella regressione lineare semplice, dove  = 1

- il valore medio del leverage è

Ne consegue anche che nella regressione lineare semplice

- la somma dei leverage di  dati è uguale a 2:

 

I valori possibili di leverage variano da un minimo di  a un massimo di 1.

Nella prassi statistica, sono giudicati alti i valori maggiori di 0,4; altri statistici suggeriscono di controllare quelli che sono oltre il doppio del valore medio.

Con i dati dell’esempio precedente, con  = 1  e 

 si ha che il valore medio di leverage è

 =

 

Sempre nella lettura dei valori di leverage, si evidenzia che essi sono massimi (0,3182) per i marziani VI e VIII, benché non siano molto maggiori del valore medio. Se ne può dedurre che

-  la retta e/o la correlazione sono calcolate, per questo aspetto, in condizioni ottimali,

-  poiché tutti i punti forniscono un contributo analogo al valore totale.

Il leverage è una potenzialità, non un peso effettivo sulla determinazione della retta di regressione e sul valore della correlazione.

 

Stime del peso effettivo sono fornite da

-  l’internally Studentized residual spesso chiamato semplicemente Studentized residual, generando confusione con quelli definiti prima nello stesso modo ma con formula differente;

-  l’externally Studentized residual chiamato anche Studentized deleted residual;

-  la distanza di Cook (Cook’s distance).

 

A differenza della simbologia utilizzata nel paragrafo precedente,

 il residuo grezzo o raw residual () del punto

 come spesso avviene può essere indicato con

 

Da esso è ricavato il residuo Studentizzato o Studentized residual 

 con

 dove

-   è la deviazione standard dei residui; con i dati dell’esempio A, è

-   è il valore di leverage del valore  relativo al residuo.

 

Nell’esempio A, dove  = 1,237

-  per il punto del marziano I  con  = +0,039  e   = 0,1000

 lo studentized residual

 è  = +0,033;

 

- per il punto del marziano VIII  con  = -0,740  e   = 0,3182

 lo studentized residual

 è  = -0,724.

(I valori dei residui studentizzati per tutti gli 11 marziani sono riportati nella tabella precedente.)

 Il valore dei residui studentizzati risulta grande, quando contemporaneamente  sono grandi

-  sia il valore del residuo ,

-  sia il valore di leverage .

 

In questo caso dello Studentized residual, la deviazione standard dei residui  è calcolata usando tutti gli  del campione; per questo motivo, con una dizione più completa e precisa,

l’indice

è noto anche come internally Studentized residual.

Ma per analizzare l’effetto degli outlier, è utilizzato spesso un altro indice studentizzato dei residui. Per ogni residuo,

- la deviazione standard   è calcolata senza il punto , cioè dopo aver tolto dal calcolo della retta e da quelli successivi per arrivare all’errore il punto .

 La simbologia della deviazione standard diventa .

Il residuo   con il nuovo denominatore

-  è indicato con

 

-  ed è chiamato externally deleted residual oppure Studentized deletd residual.

Il motivo fondamentale di questa metodologia deriva dal fatto che, se il punto  è un outlier, con la sua presenza determina un valore alto della deviazione standard .

Per costruire un test più sensibile alla scoperta dell’outlier  e eliminare il suo masking effect, è quindi opportuno non considerare i valori del punto  nel calcolo di , e successivamente utilizzare appunto la nuova deviazione standard .

 

Per il calcolo dei Studentized deletd residual, esiste un problema pratico rilevante. A pag. 137 del testo già citato Glantz e Slinker scrivono: Although most regression programs report Studentized residuals, they often do not clearly state which definition is used; to be sure, you should check the program’s documentation to see which equation is used to compute the Studentized residual.

A questo scopo e come stima più rapida degli externally Studentized residual  è opportuno utilizzare gli internally Studentized residual  (facilmente ricavabili dalla varianza d’errore dell’ANOVA, come mostrato nei paragrafi precedenti),

 mediante la relazione

 

 dove, nella statistica bivariata, = 1.

 

Spesso

-  i valori dei Studenzized residuals  

- e quelli dei corrispondenti valori Studentized deleted residuals  sono simili.

La tabella successiva mostra come per gli 11 marziani le differenze non siano molto importanti:

- solamente il valore  del marziano III da –1,778 diventa –2,081 con un aumento del 17% in valore assoluto

- e quello del marziano IX aumenta del 12 % ma partendo da un valore minore.

 

 

 

 

Tuttavia a volte sono molto differenti. In alcuni casi   (avendo ridotto la varianza d’errore) può essere molto maggiore di  (in valore assoluto).

Quale dei due valori utilizzare nel test per gli outlier?

 In questi casi,

-  con  il test sull’outlier è più prudenziale,

-  con  il test sull’outlier è più potente.

E’ ovvio che l’interesse dell’utente per uno dei due risultati può influire sulla scelta di quale residuo utilizzare.

Sempre Glantz e Slinker (a pag. 138) suggeriscono il test più potente, scrivendo: …the value of  can greatly exceed , in some instances. Thus,  is slightly preferred.