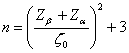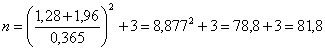CORRELAZIONE  E  COVARIANZA

 

 

18.5.   POTENZA A PRIORI E A POSTERIORI PER LA SIGNIFICATIVITA’ DI r

 

 

Le due ipotesi nulle 

-  H₀: r = 0   che indica che il valore reale di correlazione del campione è uguale a 0

-  H₀: r = r₀ che indica che il valore reale di correlazione del campione è uguale a un valore r qualsiasi, di norma diverso da 0

sono rifiutate correttamente quando nella realtà

r ¹ 0      oppure       r ¹ r₀

 il valore vero di r è diverso da 0 (zero).

Ma, in tali condizioni, la distribuzione è asimmetrica, come visto anche nella figura con l'ultimo esempio.

 

Pertanto, per il calcolo della potenza 1-b in un test di significatività del coefficiente di correlazione r, è necessario ricorrere alla trasformazione di r in z di Fisher.

I metodi di stima di 1-b presentano alcune differenze se

A)  l’ipotesi nulla è  H₀: r  =  0

B)  l’ipotesi nulla è  H₀: r  =  r₀

 

A)  Nel primo caso, nella verifica dell’ipotesi H₀: r = 0, la stima della potenza a posteriori 1-b è ottenuta dalla relazione:

dove

-   è il valore che, nella distribuzione normale unilaterale, permette di ricavare direttamente (senza trasformazione) la probabilità b;

-   è il valore critico di r, da prendere in una delle due tabelle dei valori critici di r,  per la probabilità a prefissata in una distribuzione bilaterale o unilaterale e con df n = n – 2, trasformato in z con la formula di Fisher;

-   è il valore di r sperimentale, trasformato in z con la formula di Fisher;

-   è il numero di coppie di dati,  con i quali è stato calcolato r,

-  ricordando che sia il valore critico di r sia il valore sperimentale di r devono essere trasformati con la solita formula

 

Sempre per rifiutare l’ipotesi nulla H₀: r = 0 quando il valore atteso è r₀ ¹ 0,

 la potenza a priori o numero minimo n di dati perché il valore campionario r sia significativo

 è

 dove

-   e  sono i valori di z nella distribuzione normale per le probabilità  a e b (senza trasformazione di Fisher),

-   (zeta greca minuscola) è il valore  atteso, trasformato in z secondo Fisher.

 

ESEMPIO 1. (PER L'IPOTESI H₀: r = 0)    Con 20 dati è stato calcolato un valore di r = 0,35 che non è risultato significativamente diverso da zero, alla probabilità a = 0.05. Infatti, nelle due tabelle relative è semplice osservare che il valore critico alla stessa probabilità a = 0.05 in un test bilaterale con df = 18  è 0,4438.  Si chiede:

a) quale è la potenza di questo test?

b) quante coppie di dati(n) occorre raccogliere, per rifiutare l’ipotesi nulla H₀: r = 0 nel 90% dei casi, al livello di significatività del 5%?

 

Risposte.

Per il primo caso,

a) Applicando la formula

dove

-   è il valore nella distribuzione normale unilaterale che permette di ricavare direttamente la probabilità b;

-   è il valore sperimentale di r (uguale a 0,35), che trasformato in z con il metodo di Fisher

 

 

 risulta uguale a 0,365

 

-   è il valore critico di r, alla probabilità a = 0.05 bilaterale con n = n - 2 = 18 (nella tabella relativa è 0,4438); trasformato in z con il metodo di Fisher

 

 

 risulta uguale a 0,477.

 

Con i dati dell’esempio,

  risulta uguale a 0,46.

 

Nella distribuzione normale unilaterale, ad essa corrisponde una probabilità b = 0,323. Il segno indica solo la coda della distribuzione.

Di conseguenza, la potenza 1-b del test è 1-0,323 = 0,677 o 67,7%

 

 

b)  Per stimare quanti dati n sono necessari per un test con b = 0.10 e a = 0.05 bilaterale, affinché un valore atteso di r = 0,35 risulti significativamente diverso da zero,

 usando la formula

 dove con

-   = 1,28 (in una distribuzione normale unilaterale per una probabilità uguale a 0.10),

-   = 1,96 (in una distribuzione normale bilaterale per una probabilità uguale a 0.05),

-   = 0,365 ottenuto dalla trasformazione di r = 0,35

 mediante

 si ottiene

 un valore di n = 81,8. E’ necessario rilevare almeno 82 coppie di dati.

 

 

Nel secondo caso, quando l’ipotesi nulla è  H₀: r = r₀ dove r₀ ¹ 0,

 la formula per calcolare la potenza a posteriori 1-b è leggermente più complessa di quella precedente, diventando

 dove, mantenendo uguali gli altri parametri,

-   in

-   z è il valore campionario di r trasformato in z con la formula di Fisher

-    (zeta greca minuscola) è  la stessa trasformazione del valore r₀ atteso o ipotizzato,

ricordando che i tre valori entro parentesi, cioè (1) il valore sperimentale di r, (2) il valore atteso o teorico di confronto r_0,  (3) il valore critico di r con df n-2 devono essere trasformati con la formula di Fisher.

 

 

ESEMPIO 2  (PER L'IPOTESI  H₀: r = r₀  DOVE  r₀ ¹ 0)    La correlazione  tra le variabili X₁ e X₂  è stata valutata in r = 0,15. Con 100 dati, un ricercatore ha calcolato r = 0,35 e ha motivo di credere che, nella nuova condizione sperimentale, la correlazione sia significativamente maggiore.

Calcolare la potenza del test, per una significatività a = 0.05.

 

Risposta

1)  Con r = 0,35 il valore di z

 

 

 è uguale a 0,365.

 

2)  Con r₀ = 0,15 il valore di  

 

 

 è  uguale a 0,151,

 

3) Il valore critico di r alla probabilità a = 0.5 in una distribuzione unilaterale con df = 98 non è riportato nelle 2 tabelle specifiche. Per interpolazione tra 0,168 con df 95  e  0,164 con df 100 può essere stimato uguale a 0,165. Da esso si ricava

 il valore di  

 

 

 che risulta uguale a 0,166.

 

4) Da questi tre valori e con n = 100, si ottiene

 

 

 un valore di = 0,47

In una distribuzione normale unilaterale, a z = 0,47 corrisponde una probabilità di 0,316.

Con questi dati, il valore di b è uguale a 0,316 e la potenza 1-b del test richiesto è 1-0,316 = 0,684.