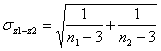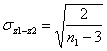CORRELAZIONE  E  COVARIANZA

 

 

18.6.   DIFFERENZA TRA DUE COEFFICIENTI DI CORRELAZIONE, IN CAMPIONI INDIPENDENTI;  CALCOLO DEL COEFFICIENTE COMUNE

 

Il confronto tra due coefficienti di correlazione r₁ e r₂, calcolati su due campioni indipendenti, per verificare

 l’ipotesi nulla

H₀: r₁ = r₂

 con ipotesi alternativa sia bilaterale

H₁: r₁ ¹ r₂

 che unilaterale

H₁: r₁ < r₂     oppure      H₁: r₁ >  r₂

 pone sempre il problema della forte asimmetria dei valori campionari alla quale si aggiunge quella della non omogeneità delle due varianze.

La simmetria e la omoschedasticità  sono ricostruite mediante la trasformazione di Fisher, per cui il test diventa

dove

-   Z è il valore della distribuzione normale, unilaterale o bilaterale in rapporto all’ipotesi alternativa,

-    e  sono r₁ e r₂ trasformati con la formula di Fisher,

-    è l’errore standard della differenza precedente, ottenuta

 con

come formula generale e

 con la formula semplificata

 quando i due campioni sono bilanciati(n₁ = n₂)

Con poche decine di dati, all’uso della distribuzione normale alcuni preferiscono l’uso della tabella t con df = N-4, in quanto più cautelativa. Permane il problema che solitamente i testi per la distribuzione t riportano solo le tavole sinottiche; quindi risulta impossibile stimare la probabilità in modo più preciso.

 

 

Nel caso di due campioni dipendenti, come possono essere i coefficienti di correlazione del padre e quello della madre con una caratteristica di un figlio, calcolate su varie coppie di genitori, la procedura è differente.

 

 

Se i due coefficienti di correlazione r₁ e r₂ non risultano significativamente differenti, anche sulla base della potenza del test e delle dimensioni del campione si può concludere che r₁ = r₂. In tali condizioni, spesso è utile calcolare un coefficiente di correlazione comune o pesato (common or weighted correlation coefficient); è la misura più corretta della correlazione tra le variabili X₁ e X₂, in quanto media ponderata dei risultati dei due esperimenti.

Sempre per i problemi di simmetria e omoschedasticità,  per ottenere il coefficiente di regressione comune r_w

-  dopo la trasformazione di r₁ e r₂ rispettivamente in z₁ e z₂

-  si calcola il valore medio z_w

 con

 

 che, nel caso di n₁ = n_{2 ,} può essere semplificata in

 

-  Infine si trasforma z_w in r_w

con

 

Recentemente, sono stati proposti altri metodi, che dovrebbero dare stime più precise di r_w.

 

 

ESEMPIO

a) Calcolare la significatività della differenza tra i due coefficienti di correlazione

-   r₁ = 0,22 con n₁ = 30 e

-   r₂ = 0,31 con n₂ = 50

b) Calcolare inoltre il coefficiente di correlazione ponderato r_w.

 

Risposte

a)  Dopo aver trasformato r₁= 0,22

 

 

 in z₁ = 0,224

 e r₂ = 0,31

 

 

in z₂ = 0,321

-  si calcola l’errore standard della differenza z₁-z₂

 

 

 ottenendo = 0,24.

Da essi si ricava

 un valore di Z = -0,40.

Nella distribuzione normale bilaterale, poiché la domanda verte solo sulla significatività della differenza tra i due coefficienti di correlazione r₁ e r₂, a Z = -0,40 corrisponde una probabilità a = 0,689. Pure senza un’analisi della potenza del test, illustrata nel paragrafo successivo, la probabilità è così alta che si può concludere non esiste alcuna differenza tra i due coefficienti angolari.

 

Nel caso di un test unilaterale, rispetto alla procedura illustrata l’unica differenza consiste nella stima della probabilità a, non diversamente dal test t su due medie o due coefficienti angolari.

 

 

b)   Per ottenere il coefficiente ponderato r_w, con

-  z₁ = 0,224   e   n₁ = 30

-  z₂ = 0,321   e   n₂ = 50

 

-  dapprima si stima z_w

 

 

che risulta uguale a 0,286

-  infine con la trasformazione

 

 

si ricava r_w = 0,278.

Il coefficiente di correlazione comune o ponderato tra

-   r₁ = 0,22 con n₁ = 30  e

-   r₂ = 0,31 con n₂ = 50

 è r_w  = 0,278.