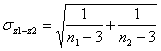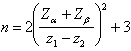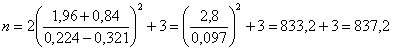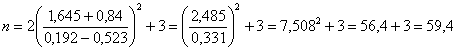CORRELAZIONE  E  COVARIANZA

 

 

 

18.7.   POTENZA A PRIORI E A POSTERIORI DEL TEST PER LA SIGNIFICATIVITA’ DELLA DIFFERENZA TRA DUE COEFFICIENTI DI CORRELAZIONE

 

 

La potenza a posteriori 1-b del test di significatività tra due coefficienti di correlazione in campioni indipendenti è valutata

 mediante

-  dove, con la solita simbologia,

-   e  sono r₁ e r₂ trasformati con la formula di Fisher,

-   è l’errore standard della differenza precedente, ottenuta

 con

 

-    è il valore di Z che permette di ricavare la probabilità b in una distribuzione normale unilaterale,

-    è il valore ricavato dalle tabella sulla base della probabilità a prefissata nella stessa distribuzione normale, ma unilaterale o bilaterale in rapporto alla direzione dell’ipotesi H₁.

 

 

La potenza a priori o numero minimo di coppie di osservazioni (n) può essere valutata

 con

 utilizzando la simbologia consueta.

Come nel test t, la quantità n indica il numero minimo di dati per ognuno dei due coefficienti di correlazione a confronto, affinché l’ipotesi nulla r₁ = r₂ possa essere rifiutata alla probabilità a prefissata e con la potenza 1-b desiderata.

Il bilanciamento di due campioni indipendenti permette di raggiungere la potenza massima del test, utilizzando il numero minimo di osservazioni per ogni gruppo. Ma nella pratica sperimentale, non sempre le rilevazioni nei due gruppi hanno lo stesso costo morale od economico: somministrare sostanze tossiche aumenta la mortalità delle cavie rispetto al placebo; le analisi del controllo e del trattato possono richiedere procedure differenti che esigono tempi di durata differente; tra due aree a confronto nelle quali prelevare i campioni, una può essere sul posto e l’altra molto distante. In vari settori della ricerca applicata, per valutare le trasformazioni intervenute nel periodo, è prassi richiedere il confronto di dati ancora da raccogliere rispetto a dati storici, il cui campione ovviamente non può essere ampliato.

Spesso, può essere utile diminuire al minimo le osservazioni di un gruppo oppure utilizzare il piccolo campione già raccolto, aumentando ovviamente quelle dell’altro gruppo, affinché il test non perda la potenza desiderata.

 

La media armonica permette di stimare

-   quante osservazioni deve avere il campione 2 (n₂),

-   una volta che sia stato stimato il numero minimo di dati (n) e

-   prefissato il numero di dati che si intende raccogliere o già raccolti per il campione 1 (n₁)

 mediante la relazione

 

 

ESEMPIO 1

Il precedente test per la significatività della differenza tra i due coefficienti di correlazione

-   r₁ = 0,22 con n₁ = 30

-   r₂ = 0,31 con n₂ = 50

 non ha permesso di rifiutare l’ipotesi nulla.

 Si chiede

a) Quale era la potenza di questo test per una significatività con  a = 0.05?

b) Quanti dati per gruppo sarebbero necessari affinché nel 80% dei casi il test risulti significativo alla probabilità a = 0.05?

Risposte

A)  Dapprima  si trasformano r₁= 0,22

 

 

 in z₁ = 0,224

 e r₂ = 0,31

 

 

in z₂ = 0,321

 Successivamente si calcola l’errore standard della differenza z₁-z₂

 

 

 ottenendo = 0,24

 e nella tabella della distribuzione normale bilaterale per  a = 0.05 si rileva Z = 1,96.

Infine con

 

 si ottiene Z_b = - 1,56

Ad un valore di Z = 1,56 in una distribuzione normale unilaterale corrisponde una probabilità uguale 0,059; ma il valore negativo indica che essa si trova a sinistra della distribuzione, molto distante dal valore dell’ipotesi nulla; di conseguenza, la potenza del test è particolarmente bassa, pari appunto al 5,9%.

 

 B) Una conferma di questa potenza a posteriori molto bassa può venire anche dalla stima della potenza a priori o numero minimo di dati necessari affinché il test sulla differenza tra i due coefficienti di correlazione risulti significativo. Con una potenza così bassa, ovviamente il numero (n) richiesto risulterà molto alto.

Poiché,

-   per una probabilità  a = 0.05 bilaterale,  il valore di Z_a  è uguale a  1,96

-   mentre, per una probabilità b = 0.20 unilaterale, il valore di Z_b è uguale a 0,84

 e con z₁ = 0,224   e   z₂ = 0,321

 il numero minimo di dati per ogni per ogni gruppo

 

 

 è n = 838 (sempre arrotondato all’unità superiore).

Il numero stimato è molto maggiore di quello dei dati raccolti nei due campioni (30 e 50). In vari settori della ricerca applicata, nei quali ogni misura campionaria ha costi non trascurabili, un numero così elevato indica l’impossibilità pratica di dimostrare la significatività della differenza tra i due coefficienti di correlazione. Pertanto, si può ritenere che tra essi non esista una differenza significativa, come d’altronde indicava il valore di probabilità a molto alto.

 

 

ESEMPIO 2.  Un ricercatore dispone di un campione di 40 osservazioni, raccolte in una rilevazione di alcuni anni prima, nel quale il coefficiente di correlazione lineare semplice sulle quantità di due componenti chimici di un alimento è risultato uguale a 0,19. Egli si aspetta che, per le trasformazioni intervenute nell’ultimo periodo nella coltivazione e nella conservazione dei cibi, tale correlazione sia aumentata. Con un campione di 30 misure ha infatti trovato un valore di r = 0,48.

Calcolare:

a) Quanti dati servono, per un esperimento con 2 campioni bilanciati, affinché il test risulti significativo alla probabilità a = 0.05 con un rischio di commettere un errore di II Tipo pari a una probabilità b = 0.20?

b) Poiché il campione storico è di 40 dati, quanti ne deve raccogliere con il secondo campione per rispettare le probabilità a e b precedenti?

 

Risposte

Dopo aver effettuato il test di significatività, poiché se esso risultasse positivo il problema sarebbe già risolto, si stima il numero di dati minimo per ognuno dei due gruppi a confronto.

-   Dapprima si trasforma r₁ = 0,19 in z₁

 

 ottenendo z₁ = 0,192

 e r₂ = 0,48 in z₂

 

 

 ottenendo z₂ = 0,523.

-   Successivamente, dalla distribuzione normale si ricava

 il valore di Z per a = 0.05 unilaterale (perché il test chiede se vi è stato un aumento significativo) ottenendo Z_a = 1,645

 e il valore di Z per b = 0.20 unilaterale ottenendo Z_b = 0,84.

-   Infine di ricava n

 

 

 che risulta uguale a 60.

 

Poiché è risultato un campione (n = 60) non molto più grande di n₁ = 40, è possibile stimare il numero di dati necessario nel secondo (n₂) per mantenere costante le probabilità richieste.

Applicando

 risulta

 che il secondo campione  deve contenere almeno n₂ = 94

E’ una risposta che, per il numero non eccessivamente elevato di dati richiesti rispetto al campione già raccolto, rende possibile l’esperimento. Ad esempio, se il numero (n) di dati richiesto per ogni gruppo  fosse stato oltre il doppio degli n₁= 40 già raccolti con il primo campione, il numero di dati da raccogliere con il secondo (n₂) sarebbe stato molto grande, tale da rendere molto costoso, se non impossibile, l’esperimento. Inoltre con due campioni così sbilanciati, le condizioni di potenza e significatività  del test sarebbero state profonde alterate.

Per altri concetti sul bilanciamento di due campioni indipendenti, si rinvia al capito sul test t, in quanto la procedura è simile.