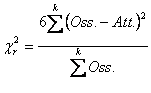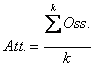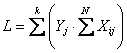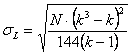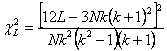|
TEST NON PARAMETRICI PER IL TREND
19.5. IL TEST DI PAGE O DELLE ALTERNATIVE ORDINATE IN K CAMPIONI DIPENDENTI
Il test di Page è simile al test di Jonckheere, ma serve quando le rilevazioni dei dati sono condotte in modo programmato, tale che i k gruppi a confronto abbiano osservazioni raccolte nelle stesse condizioni. Nell’analisi della varianza con la quale condivide l’ipotesi nulla H0: me1 = me2 = … = mek è il caso di k campioni dipendenti o a blocchi randomizzati I dati devono essere impostati in una tabella a doppia entrata:
Questo test, derivato da quello di Friedman già noto come distribution-free test for ordered alternatives based on Friedman rank sums, è stato proposto da Ellis Batten Page dell’Università del Connecticut nel 1963 con l’articolo Ordered hypotheses for multiple treatments: a significance test for linear ranks (pubblicato sulla rivista Journal of the American Statistical Association Vol. 58, pp. 216-230). Il test di Page, come il test di Friedman, serve per verificare l'ipotesi nulla
ma contro l’ipotesi alternativa unilaterale
o con un ordine delle mediane opposto. Nel riassunto del suo articolo, Page scrive: A ranking statistic L is presented as test of a monotonic relationship among the treatment groups in the two-way analysis of variance. Il test è solo unilaterale e quindi occorre definire a priori l’ordine o rango atteso dei valori delle mediane. E’ quindi più potente del test di Friedman. Accettare l'ipotesi
alternativa Per proporre il metodo, evidenziando affinità e differenze con il test di Friedman, Page presenta la seguente tabella di un esperimento fittizio
(In realtà Page indica con n il numero di trattamenti e con m il numero di righe; ma per utilizzare la stessa simbologia usata nei test precedenti, anche qui è usato k per il numero di trattamenti e N per quello delle righe) Il test di significatività utilizza il c2. Tale verifica è stata introdotta nel 1937 da Milton Friedman con l’articolo The use of ranks to avoid the assumption of normality implicit in the analysis of variance (pubblicato su Journal of the American Statistical Association, Vol. 32 pp. 675-701) e sviluppata nel 1940 con l’articolo A comparison of alternative tests of significance for the test of m rankings (pubblicato su Annals of Mathematical Statistics, Vol. 11, pp. 86-92). Successivamente è stata esaminata da altri, tra i quali M. G. Kendall e B. B. Smith nel 1939 con l’articolo The problem of m rankings (pubblicato su Annals of Mathematical Statistics, Vol. 10, pp. 275-287). La formula generale
applicata ai ranghi diventa
dove i gdl sono N – 1 e il valore atteso è
Con i dati dell’esempio riportato da Page dove
si ottiene c2 = 6,60 con 3 gdl. Il test non risulta significativo,
poiché il valore critico alla probabilità a = 0.05 è In questo caso, il test di Friedman non permette di rifiutare l’ipotesi nulla. Ellis Batten Page propone la statistica
dove Yj è il rango della colonna. Con i dati dell’esempio
si ottiene L = 168 I valori critici sono forniti direttamente dalla Page nell’articolo citato. Essi sono riportati nelle tabelle seguenti, con variazioni che riguardano solo la impostazione grafica.
Nel caso di piccoli campioni, la significatività di L è fornita solo dalle tabelle. L’entrata è determinata - dal numero di colonne o gruppi (k) e - dal numero di dati (N) in ogni colonna. Con i dati dell’esempio, in cui k = 4 e N = 6, la tabella dei valori critici alla probabilità - a = 0.05 riporta un valore uguale a 163 - a = 0.01 riporta un valore uguale a 167 - a = 0.001 riporta un valore uguale a 172 Avendo calcolato L = 168 nel caso dell’esempio precedente è possibile rifiutare l’ipotesi nulla con probabilità P < 0.01. E’ da evidenziare che con il test di Friedman non si rifiutava l’ipotesi nulla nemmeno alla probabilità a = 0.05.
Nel caso di grandi campioni, la statistica L si distribuisce in modo approssimativamente normale
dove, in tabelle a doppia entrata di - k trattamenti o colonne , - N righe o osservazioni per colonna, la media attesa
e
Valori critici di L proposti da Page (Sono significativi i valori uguali o maggiori di quelli riportati alle probabilità prefissate) I valori per campioni piccoli, riportati entro caselle sono basati su distribuzioni esatte. I valori per campioni grandi, riportati senza casella, sono basati su approssimazioni alla normale
(continua) Valori critici di L proposti da Page (Sono significativi i valori uguali o maggiori di quelli riportati alle probabilità prefissate) I valori per campioni piccoli, riportati entro caselle sono basati su distribuzioni esatte. I valori per campioni grandi, riportati senza casella, sono basati su approssimazioni alla normale
(continua) Valori critici di L proposti da Page (Sono significativi i valori uguali o maggiori di quelli riportati alle probabilità prefissate) I valori per campioni piccoli, riportati entro caselle sono basati su distribuzioni esatte. I valori per campioni grandi, riportati senza casella, sono basati su approssimazioni alla normale
Sostituendo in
e semplificando, si ottiene la formula abbreviata
che permette un calcolo più rapido e semplice del valore di Z. Poiché il test di Page è a una coda, i valori critici fondamentali sono: - Z = 1,645 alla probabilità a = 0.05 - Z = 2,328 alla probabilità a = 0.01 - Z = 3,09 alla probabilità a = 0.001
Nelle precedenti tabelle dei valori critici, entro le caselle sono riportati i valori stimati con il metodo esatto, valido per campioni piccoli. Nella zone senza le caselle, sono riportati i valori ricavati con la distribuzione normale, valida per grandi campioni. Pubblicati dalla Page fino a campioni di dimensioni k = 10 e N = 50, questi valori permettono di verificare la significatività di L senza l’uso della normale. Il ricorso alla distribuzione Z unilaterale ha lo svantaggio di richiedere calcoli molto più lunghi, per passare da L a Z, ma il vantaggio di determinare probabilità P più precise.
Per spiegare la metodologia in modo ancora più semplice e illustrare altri concetti importanti nell’applicazione del test, è utile sviluppare un esempio in tutti i suoi passaggi logici e metodologici.
ESEMPIO 1. Si supponga di voler sperimentare gli effetti di una sostanza tossica sulla crescita di una specie vegetale. A questo scopo, sono stati collocati i semi - in 5 colture con concentrazione crescente (36, 54, 72, 108, 144) del principio attivo e - il test è stato ripetuto da 3 ricercatori (A, B, C). Nella tabella sottostante sono riportati i valori medi delle 4 repliche fatte da ogni ricercatore per ogni concentrazione (l’uso di valori medi vieta l’uso della statistica parametrica):
E’ possibile affermare che l’aumento della concentrazione della sostanza tossica (da 36 a 144) inibisce la crescita della specie?
Risposta. La metodologia inferenziale del test di Page richiede alcuni passaggi.
1 – Dapprima si deve formulare l’ipotesi nulla H0: me36 = me54 = me72 = me108 = me104 secondo la quale le mediana della crescita alle 5 diverse concentrazioni sono uguali e l’ipotesi alternativa unilaterale H1: me144 £ me108 £ me72 £ me54 £ me36 secondo la quale la crescita della specie aumenta con il diminuire della concentrazione.
2 – L’ipotesi alternativa definisce l’ordine con il quale devono essere riportati i dati nella tabella. Con i dati dell’esempio, è necessario invertire l’ordine delle colonne (i trattamenti a confronto), che pertanto diventa
3 – Come nel test di Friedman, i valori devono essere trasformati nel loro rango, entro la stessa riga. Si assegna quindi il rango minore (1) al punteggio più basso e si aumenta di 1 per ogni punteggio successivo della stessa riga fino a k, uguale al numero di trattamenti o gruppi a confronto. Nel caso di due o più valori uguali entro la stessa riga, secondo la procedura abituale, il punteggio viene calcolato sulla media dei loro ranghi.
Con i dati dell’esempio, la trasformazione dei valori in ranghi delle tre prime righe e la loro somma, riportata nella quarta riga, diventa
4 - Il test
utilizza i totali dei ranghi Se è vera l'ipotesi nulla H0, i punteggi saranno distribuiti a caso entro la stessa riga e pertanto le somme dei ranghi (Rj) per colonna tenderanno ad essere uguali. Questi valori dipenderanno dal numero N di dati presenti in ogni colonna.
5 - Nel test di
Page, dalla somma degli
Con i dati dell’esempio L = 1 x 5 + 2 x 5 + 3 x 9 + 4 x 14 + 5 x 12 = 5 + 10 + 27 + 56 + 60 = 158 L risulta uguale a 158.
6 - Nel caso di piccoli campioni, la significatività di L è fornita dalle tabelle. L’entrata è determinata - dal numero di colonne o gruppi (k) e - dal numero di dati (N) in ogni colonna. Con i dati dell’esempio, in cui k = 5 e N = 3, la tabella dei valori critici alla probabilità - a = 0.05 riporta un valore uguale a 150 - a = 0.01 riporta un valore uguale a 155 - a = 0.001 riporta un valore uguale a 160 Poiché il valore calcolato è L = 158, si rifiuta l’ipotesi nulla con probabilità P < 0.01. E’ importante osservare come l’affermazione riguardi il trend generale, cioè la diminuzione dei valori medi di crescita nel loro complesso, non tutti i risultati dei trattamenti; infatti la crescita media è stata maggiore con dose 54 rispetto a dose 36.
TIES. I dati dovrebbero essere misurati su una scala continua, per cui non dovrebbero esistere valori con lo stesso rango. Page non ha proposto correzioni per i ties, affermando che la scala deve essere continua. Tuttavia un numero molto limitato di valori sono accettabili, poiché non alterano sensibilmente il risultato e forniscono una risposta più cautelativa. In altri termini l’errore che si commette con i ties rende il test meno significativo
Nel caso di 2 soli gruppi (k = 2), l’alternativa al test di Page è il test U di Mann-Whitney per 2 campioni dipendenti, nell’ipotesi unidirezionale (Infatti verifica la direzione della tendenza centrale con due gruppi).
Nelle situazioni in cui i trattamenti hanno un ordine naturale, il test di Page è preferibile a quello di Friedman, che risponde solo alla domanda se le mediane dei vari trattamenti sono differenti. Una volta che sia stata rifiutata l’ipotesi nulla, per ottenere una informazione più completa sulla serie delle mediane, è possibile verificare tra quali esista una differenza significativa, ricorrendo ai confronti multipli basati sulla somma dei ranghi di Friedman.
Esempio 2 (per Grandi Campioni). Lungo il corso d'acqua che attraversa una città, sono state collocate 6 stazioni (A, B, C, D, E, F) di rilevazione dell'inquinamento. In ognuna delle 6 stazioni, per 15 giorni è stata fatta una misura del carico inquinante. I valori campionati, classificati per stazione e per giorno di rilevazione, sono riportati nella tabella a due entrate:
Si intende verificare se, con l’accumulo degli scarichi urbani, lungo il percorso (dalla stazione A alla F) si ha un aumento significativo del carico inquinante.
Risposta. 1 - Dapprima si devono definire l'ipotesi nulla
e l'ipotesi alternativa
intendendo con essa che tra valore iniziale e valore finale c’è almeno una discontinuità significativa.
2 - Successivamente, poiché i trattamenti sono già nell’ordine naturale, si devono trasformare i valori in ranghi, considerando in modo indipendente ogni riga, come nella tabella sottostante:
3 - Successivamente, si calcolano le somme dei ranghi per colonna (Rj), come nell’ultima riga della tabella precedente.
4 - Dalla somma dei ranghi per colonna (Rj) si ottiene il valore di L
che risulta uguale a 1321. 5 - Per valutare la sua significatività,
si stima il valore di
che risulta uguale a 7,20. Il valore di Pertanto, si rifiuta l'ipotesi nulla e si accetta l'ipotesi alternativa: dalla stazione A alla stazione F si ha un aumento altamente significativo del carico inquinante, anche se non è possibile dire nulla sulla curva di crescita. Nella tabella dei valori critici, con k = 6 e N = 15 alla probabilità a = 0.001 è riportato L = 1197. Permette di rifiutare l’ipotesi nulla con probabilità P < 0.001 quindi con una stima molto meno precisa. Infine l’eventuale ricorso ai confronti multipli con il test di Friedman permette di verificare tra quali stazioni esiste una differenza significativa.
Esempio 3 (per Piccoli Campioni). In un centro urbano sono stati attivati 5 punti di osservazione (a, b, c, d, e) per rilevare l'inquinamento dovuto al traffico e per ogni zona sono state effettuate 4 osservazioni, a distanza di 4 ore ognuna, dalle ore 6 alle ore 18. Per esporre alla cittadinanza la situazione dell’inquinamento atmosferico in modo chiaro e sintetico, l’ufficio comunale ha fornito le misure su una scala ordinale, con giudizi della qualità dell'aria riportati in modo simbolico, -- pessima - insufficiente = sufficiente + buona ++ ottima come nella tabella sottostante
Si vuole verificare se, nel corso di una giornata con blocco del traffico, dal mattino alla sera vi è stata una diminuzione nei tassi d'inquinamento.
Risposta. I dati devono essere - trasformati in ranghi entro la stessa riga e - sommati per colonna (Rj),
al fine di calcolare il valore di L L = 1x6,5 + 2x13 + 3x14 + 4x17,5 = 144,5 che risulta uguale a 144,5.
Per k = 4 e N = 5, la tabella sinottica dei valori critici della L di Page riporta - alla probabilità a = 0.05 il valore 137 - alla probabilità a = 0.01 il valore 141 - alla probabilità a = 0.001 il valore 145. Il valore di L calcolato (144,5) è compreso tra quello relativo alla probabilità a = 0.01 e quello alla probabilità a = 0.001. Di conseguenza, si rifiuta l'ipotesi nulla con probabilità P < 0.01 di commettere un errore di I tipo. Si accetta l'ipotesi alternativa: nel complesso delle stazioni esiste un miglioramento delle condizioni dell'aria al trascorrere delle ore (dalle 6 alle 18), durante la giornata di blocco del traffico.
ESEMPIO 4 (CONFRONTI TRA L E Z). E’ ovvio che, quando il campione non è troppo piccolo, in tutti i test non parametrici esista corrispondenza tra le probabilità indicate dai valori critici riportate nelle tabelle sinottiche e quelle stimate con la distribuzione normale. E’ una relazione che spesso sfugge allo studente e al ricercatore, che non abbiano acquisito sufficiente familiarità con la statistica. A questo scopo, è didatticamente utile l’esercizio di valutare le probabilità corrispondenti ai valori critici.
Per il test di Page dalla tabella dei valori critici ricaviamo che per k uguale a 10 ed N uguale a 12, - alla probabilità a = 0.05 il valore critico è L = 3788, - alla probabilità a = 0.01 è L = 3852, - alla probabilità a = 0.001 è L = 3927. Poiché (con k uguale a 10 ed N uguale a 12) il campione è di dimensioni relativamente grandi, le probabilità calcolate con la distribuzione normale, ovviamente solo in una coda come richiede il test, dovrebbero essere molto simili.
Infatti la formula generale
per N = 12 e k = 10 diventa Z =
nella quale l’unico valore da inserire è L, fornito dalle tabelle.
Per la probabilità a = 0.05 il valore critico di L è 3788; con esso, il risultato di Z diviene
Z =
uguale a 1,66. Nella tabella dei valori critici in una coda della distribuzione normale, a Z = 1,66 corrisponde la probabilità a = 0.0485. E’ un valore molto vicino a 0.05 indicato per la significatività di L.
Per la probabilità a = 0.01 a L si sostituisce il valore critico di 3852; il risultato di Z diviene
Z =
uguale a 2,33 al quale, in una coda della distribuzione, corrisponde la probabilità a = 0.099.
Per la probabilità a = 0.001 a L si sostituisce il valore critico di 3927; il risultato di Z diviene
Z =
uguale a 3,11 al quale corrisponde la probabilità a = 0.00099. Con la distribuzione normale, i valori critici hanno fornito probabilità molto vicine, quasi coincidenti, con quelle riportate nella tabella. E’ una dimostrazione empirica del fatto che, in assenza dei valori critici, il ricorso alla distribuzione normale fornisce risposte attendibili, se i campioni non sono eccessivamente piccoli. Per campioni di dimensioni maggiori, la coincidenza è perfetta, a meno delle approssimazioni introdotte nei calcoli. Infatti la Page stima i valori critici di L fino a N = 50 e k = 10 utilizzando i valori critici di Z. Ad esempio per a = 0.01 suggerisce la misura approssimata Z = 2,33.
Per valutare la significatività di L in grandi campioni, Page suggerisce
che è distribuito approssimativamente come un chi-quadrato con 1 grado di libertà. Ma il chi-quadrato serve per test bilaterali, mentre il test di Page è unilaterale: di conseguenza la probabilità stimata con il chi-quadrato deve essere dimezzata.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||