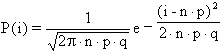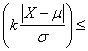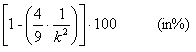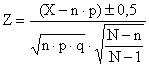|
DISTRIBUZIONI e leggi di probabilità'
2.4. alcune distribuzioni continue
Tutti i modelli precedenti forniscono la distribuzione teorica di variabili casuali discrete. Quando si devono descrivere variabili casuali continue e positive, come peso, altezza, reddito, tempo, i modelli più utili sono quelli di seguito riportati. Tra essi, la distribuzione più frequente e di maggiore utilità nella ricerca sperimentale, fondamento della statistica parametrica, è la distribuzione normale o gaussiana.
2.4.1 DISTRIBUZIONE NORMALE O DI GAUSS La più importante distribuzione continua è la curva normale. E’ stata individuata per la prima volta nel 1733 da Abraham De Moivre (nato in Francia nel 1667, vissuto in Inghilterra e morto nel 1754, la cui opera più importante The Doctrine of Chance contiene la teoria della probabilità enunciata nel 1718) ed è stata proposta nel 11797 da Karl Friedrich Gauss (tedesco, nato nel 1777 e morto nel 1855, ha scritto i suoi lavori più importanti su gravità, magnetismo e elettricità) nell'ambito della teoria degli errori. Nella letteratura francese è attribuita anche a Laplace (1812), che ne avrebbe definito le proprietà principali prima della trattazione più completa fatta da Gauss in varie riprese, a partire dal 1809.
La teoria della stima degli errori è fondata empiricamente sul fatto che tutte le misure ripetute dello stesso fenomeno manifestano una variabilità, che è dovuta all'errore commesso ogni volta. Nei calcoli astronomici, l'indicazione della posizione di ogni stella è sottoposta a un errore e la distribuzione delle medie campionarie, secondo Gauss, è di tipo normale. Da tempo, in realtà viene chiamato il dogma della normalità degli errori, poiché questa supposta normalità della distribuzione non ha una dimostrazione, ma solo qualche verifica empirica. D'altronde, se il problema è indicare esattamente dove si trovi la stella, la soluzione è impossibile, a meno che esista una distribuzione nota degli errori. Se essi hanno una distribuzione normale, è semplice indicare che la zona in cui con probabilità maggiore la stella si trova: è collocata simmetricamente intorno alla media di tutte le medie campionarie. E' il centro della distribuzione di tutte le misure e con le leggi della distribuzione normale è possibile stimare anche la probabilità con la quale si trova entro un intervallo prestabilito, collocato simmetricamente intorno alla media della distribuzione normale.
Il nome di curva normale deriva d alla convinzione, non sempre corretta, che molti fenomeni, da quelli biologici e quelli fisici, normalmente si distribuiscano secondo la curva gaussiana. La sua denominazione di curva degli errori accidentali, diffusa soprattutto nelle discipline fisiche, deriva dall'osservazione sperimentale che la distribuzione degli errori, commessi quando si misura ripetutamente la stessa grandezza, è molto bene approssimata da tale curva. Sotto l'aspetto matematico, la distribuzione gaussiana può essere considerata come il limite della distribuzione binomiale - per n che tende all'infinito, - mentre né p né q tendono a 0 (condizione che la differenzia dalla poissoniana).
Se n tende all'infinito e p resta costante, la media (n×p) a sua volta si approssima all'infinito e rende la distribuzione senza applicazioni pratiche. Per contro, la variabile considerata, che nel caso di pochi dati era quantificata per unità discrete, può essere espressa in unità sempre minori, tanto che diventa accettabile esprimerla come una grandezza continua. La distribuzione gaussiana può essere considerata il limite anche della distribuzione poissoniana, quando i e m diventano molto grandi.
Quando n tende all'infinito (in realtà quando n, i e m sono molto grandi) a condizione che né p né q tendano a 0, secondo il teorema di De Moivre (1833) la probabilità Pi della distribuzione binomiale è sempre meglio approssimata da
Sostituendo n×p con la media m della popolazione, n×p×q con la varianza s2 della popolazione e il conteggio i (indice di un valore discreto) con x (indice di una misura continua), si ottiene
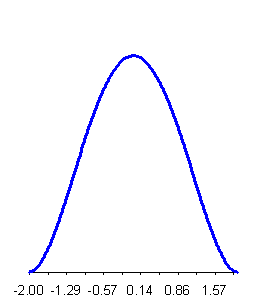
che è l'espressione della funzione di densità di probabilità (o delle frequenze relative) della distribuzione normale. In termini meno matematici, permette di stimare il valore di Y (il valore dell’ordinata o altezza della curva) per ogni valore di X (il valore della ascissa). La curva normale ha la forma rappresentata nella figura 10. La distribuzione normale con media µ=0 e deviazione standard s =1 è indicata con N(0,1); al variare di questi due parametri che la definiscono compiutamente, si possono avere infinite curve normali. Le
caratteristiche più importanti della normale sono una frequenza relativamente
più elevata dei valori centrali e frequenze progressivamente minori verso gli
estremi. La funzione di densità è simmetrica rispetto alla media: cresce da
zero fino alla media e poi decresce fino a
Figura 10. Distribuzione normale µ=175,
In ogni curva normale, la media, la moda e la mediana sono coincidenti. Se µ
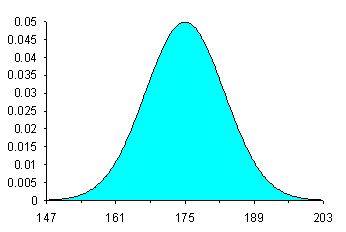
varia e Se invece µ rimane costante e s varia, tutte le infinite curve hanno lo stesso asse di simmetria; ma hanno forma più o meno appiattita, secondo il valore di s. Le due curve della figura 11 hanno media m identica e deviazione standard s differente.
Figura 11. Curve normali con µ uguale e s diversa.
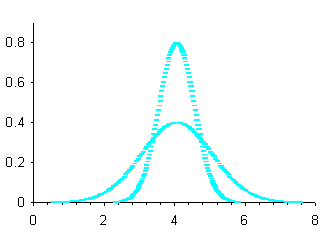
Una seconda serie di curve con medie diverse e dispersione uguale è quella riportata nella figura successiva (Fig.12).
Figura 12. Curve normali con µ diversa e s uguale.
Una terza serie è quella delle distribuzioni normali che differiscono sia per la media sia per la dispersione dei dati (figura 13).
Figura 13. Curve normali µ e s diverse.
I momenti e gli indici di forma della distribuzione normale (già presentati nel primo capitolo sulla statistica descrittiva) valutano in modo sintetico e mediante una rappresentazione numerica le sue caratteristiche essenziali, rese visibili e di più facile lettura, ma non quantificate, nella rappresentazione grafica. Poiché la distribuzione teorica normale è simmetrica, tutti i momenti di ordine dispari dalla media sono nulli. Per i momenti di ordine pari, è bene ricordare che - il momento di secondo ordine è uguale alla varianza (µ2 = s2) - ed il momento di quarto ordine è uguale a 3 volte la varianza al quadrato (µ4 = 3s4). L'indice di simmetria di Pearson risulta b1 = 0. L'indice
di curtosi di Pearson è L'indice
di simmetria di Fisher è L'indice di curtosi
di Fisher è Le infinite forme della distribuzione normale, determinate dalle combinazioni di differenze nella media e nella varianza, possono essere tutte ricondotte alla medesima forma. E’ la distribuzione normale standardizzata o normale ridotta, che è ottenuta mediante il cambiamento di variabile dato da
La standardizzazione è una trasformazione che consiste nel: - rendere la media nulla (m = 0), poiché ad ogni valore viene sottratta la media; - prendere la deviazione standard Come conseguenza, si ottiene anche una trasformazione degli scarti x-µ in scarti ridotti,
La distribuzione normale ridotta viene indicata con N(0,1)., che indica appunto una distribuzione normale con media 0 e varianza uguale a 1. Dopo il cambiamento di variabile, nella normale ridotta la densità di probabilità è data da
dove Z è il valore sull’asse delle ascisse, misurato in unità di deviazioni standard dalla media.
Y = Ordinata della curva normale standardizzata in z.
Figura 14 con tabella delle ordinate per ascisse (z) della distribuzione normale standardizzata
Tale relazione evidenzia come la forma della distribuzione non dipenda più né dalla sua media né dalla sua varianza: è sempre identica, qualunque sia la distribuzione gaussiana considerata.
La tabella riportata serve solamente per rendere veloce la stima dell’ordinata. Una volta fissato il valore di z, è possibile calcolare il valore dell’ordinata, come nell’esempio successivo per il punto individuato in ascissa da z uguale a 1. Utilizzando la formula
con i dati dell’esempio si ottiene
un valore di Y uguale a 0,2420.
La tabella precedente riporta i valori della ordinata della curva normale standardizzata in z, per z che varia da 0 a 3.99. In essa si trovano i valori delle ordinate, per valori di z riportati sommando la prima colonna (in grassetto) con la prima riga (in grassetto).
Ad esempio, per Z uguale a 1.00 si deve - individuare nella prima colonna (in grassetto) il valore 1.0 - individuare nella prima riga (in grassetto) il valore 0.00, perché la somma 1.0 + 0.00 è uguale a 1.00. Nel loro incrocio, è riportato .2420 che indica appunto il valore dell’ordinata.
Per Z uguale a 1,85 si deve - individuare nella prima colonna (in grassetto) il valore di 1.8 - individuare nella prima riga (in grassetto) il valore .05 e leggere il valore riportato al loro incrocio, uguale a .0721 che indica appunto l’ordinata per z uguale a 1,85.
2.4.2 distribuzioni asintoticamente NORMALI, CON approssimazioni E trasformazioni L'interesse per le applicazioni della distribuzione normale dipende dal fatto che molte variabili sono distribuite secondo questa legge; inoltre, è accresciuto dal fatto che varie distribuzioni, che non sono rigorosamente normali o addirittura lontane dalla normalità, possono divenirle od essere ritenute tali quando 1) certi loro parametri tendono all'infinito (leggi asintoticamente normali), 2) sono quasi normali (approssimazioni), 3) oppure mediante trasformazioni appropriate, che conducono a variabili distribuite normalmente almeno in modo approssimato (trasformazioni).
1) Come esempi di leggi asintoticamente normali si possono ricordare 3 casi già presentati nei paragrafi precedenti. a - La distribuzione binomiale (p + q)n tende alla legge di distribuzione normale, quando n tende all'infinito. b - La distribuzione poissoniana tende alla distribuzione gaussiana quando la media è elevata; in pratica superiore a 6. c - La media di n variabili aleatorie indipendenti, che singolarmente seguono una legge qualunque, segue la legge normale quando n è grande.
Non sono distribuzioni esattamente normali, ma sono considerate approssimativamente tali. E' il teorema centrale della statistica, noto anche come teorema fondamentale della convergenza stocastica o teorema di Laplace-Chebyshev-Liapounoff (spesso citato solo come teorema di Laplace): - “Qualunque sia la forma della distribuzione di n variabili casuali indipendenti (xi), la loro somma X (con X = x1 + x2 + x3 +… + xn) è asintoticamente normale, con media generale uguale alla somma delle singole medie e varianza generale uguale alla somma delle singole varianze”.
Una dimostrazione semplice può essere fornita dal lancio dei dadi. Con un solo dado, i 6 numeri hanno la stessa probabilità ed hanno una distribuzione uniforme; ma con due o più dadi, la somma dei loro numeri tende ad essere sempre più simile alla normale, all’aumentare del numero dei dadi. Se invece della somma si considera la media di n lanci, si ottengono i medesimi risultati.
2) Come esempio di approssimazione alla normale di una distribuzione non normale, è possibile ricordare che nelle popolazioni animali e vegetali abitualmente la distribuzione normale viene usata sia nello studio della massa o volume, come nello studio dell'altezza o delle dimensioni di singoli individui; ma tra essi il rapporto non è lineare e quindi queste variabili non potrebbero essere tutte contemporaneamente rappresentate con la stessa legge di distribuzione. Nella pratica, sono tutte ugualmente bene approssimate dalla distribuzione normale; quindi, per tutte indistintamente è prassi ricorrere all’uso della normale.
3) Quando i dati hanno una distribuzione differente dalla normale, spesso una semplice trasformazione conduce ad una distribuzione normale. E' il caso delle trasformazioni con la radice quadrata o cubica, oppure con il reciproco, l’elevamento a potenza o con i logaritmi. Oltre agli indici statistici sulla forma (varianza, simmetria e curtosi), che misurano come la distribuzione trasformata modifichi i suoi parametri, nella scelta del tipo di trasformazione occorre considerare anche la legge biologica o naturale che determina il fenomeno di dispersione dei dati.
Figura 15. Distribuzione lognormale
Il caso di trasformazione che ricorre forse con frequenza maggiore in biologia e nelle scienze ambientali è quella logaritmica X' = log X dove X' diviene una serie di valori distribuiti in buon accordo con la normale.
Quando la distribuzione di una variabile X ha una forma simile a quella rappresentata nella precedente figura 15, con la trasformazione logaritmica in X’ assume appunto una forma molto simile alla distribuzione normale.
Le trasformazioni dei dati, qui citate in modo estremamente sintetico con l’unico scopo di presentare il concetto di distribuzioni normali dopo trasformazione, sono numerose. Saranno presentate in modo più approfondito alla fine del secondo capitolo sull’analisi della varianza, quando si discuterà sulle condizioni di validità dei test di statistica parametrica.
La distribuzione normale di Gauss e Laplace, derivata dai loro studi sulla teoria della distribuzione degli errori d’osservazione, per lungo tempo ha occupato un posto di assoluta preminenza nella statistica. E’ stato considerato assiomatico che, con un numero elevato di osservazioni, la variabile casuale avesse una distribuzione normale. Più recentemente sono stati sollevati dubbi e critiche; alcuni critici e autori di testi di statistica sono giunti ad affermare che tale assunzione era accettata universalmente solo perché - “gli statistici sperimentali pensavano che essa derivasse da un teorema, mentre i matematici pensavano che essa fosse un fatto sperimentale”.
Benché la sua importanza sia stata ridimensionata, attualmente è diffusamente accettato che moltissime distribuzioni sono approssimativamente normali.
2.4.3 DALLA DISUGUAGLIANZA DI TCHEBYCHEFF ALL’USO DELLA DISTRIBUZIONE NORMALE Nella pratica statistica, le proprietà più utili della distribuzione normale non sono i rapporti tra ascissa ed ordinata, presentati in precedenza, ma le relazioni tra la distanza dalla media e la densità di probabilità sottesa dalla curva. In modo più semplice, è possibile definire quanti sono i dati compresi tra la media ed un determinato valore, misurando la distanza dalla media m in unità di deviazioni standard s.
La frazione dei casi compresi - fra µ+ -
quella fra µ+2 -
quella fra µ+3
In pratica, nella curva normale la quasi totalità dei dati è compresa nell'intorno della media di ampiezza 3 s.
Figura 16. Relazioni tra distanza dalla m in s e densità di probabilità sottesa dalla curva.
La relazione tra la percentuale di dati sottesi dalla curva e le dimensioni dell’intervallo tra due valori è una caratteristica di rilevante importanza nella statistica applicata: se la distribuzione è normale, è sufficiente conoscere due parametri di una serie di dati, la media m e la varianza s2 (o altro parametro da esso derivato come la deviazione standard s), per conoscere anche la sua distribuzione. Più di un secolo fa, a partire da dati sperimentali due matematici Bienaymé e Chebyshev (Jules Bienaymé francese, nato nel 1796 e morto nel 1878; Pahnuty Lvovich Chebyshev russo, nato nel 1821 e morto nel 1894, il cui cognome è ovviamente scritto in cirillico; qui è scritto secondo la pronuncia inglese, in altri testi è scritto Tchebycheff in tedesco e Cebycev secondo la pronuncia francese) avevano enunciato: in un gruppo di dati comunque distribuito, la percentuale (P) di osservazioni comprese entro la distanza di k deviazioni standard (s) intorno alla media m sono almeno
P
Per dati distribuiti in qualsiasi modo, secondo questo teorema noto come disuguaglianza di Tchebycheff, nell'intervallo compreso tra ± 2s rispetto alla media m si ha
almeno il 75% delle osservazioni, mentre tra m ± 3s si trova
almeno l’88,89% dei dati. e nell'intervallo m ± 4s si trova
almeno il 93,75% dei dati. Con questa relazione, non è possibile calcolare la quantità di osservazioni compreso nell’intervallo m ± 1s.
Questo teorema, che come principio è di notevole importanza nella statistica, in quanto giustifica perché la media e la varianza bastano nella maggior parte dei casi per descrivere la distribuzione di una variabile statistica, fornisce una stima molto approssimata. Nel 1946 Harald Cramèr (svedese, nato nel 1893 e morto nel 1985, chimico e matematico che ha dato un grande contributo allo studio del teorema del limite centrale e alle funzioni di distribuzione) ha dimostrato che, se la distribuzione è simmetrica e unimodale, la stima può essere molto più accurata. La relazione tra le dimensioni dell’intervallo intorno alla media e la distribuzione di frequenza o delle probabilità P diviene
P
La migliore è la distribuzione normale standardizzata (presentata in precedenza), che permette i calcoli più precisi e viene appunto utilizzata per questa sua caratteristica, quando la distribuzione dei dati ha tale forma.
Tabelle specifiche forniscono le frequenze sottese alla curva per ogni valore di z, ottenuto con la trasformazione in normale ridotta di qualsiasi distribuzione normale, mediante la relazione
Conoscendo Z, con esse è possibile stimare le frequenze o probabilità; con il percorso inverso, è possibile anche stimare il valore di Z partendo dalle frequenze. Per comprenderne l’uso, più di spiegazioni teoriche sono utili dimostrazioni pratiche, come quelle riportate negli esercizi seguenti.
Alla fine del capitolo ne sono state riportate 4, anche se i testi di statistica di norma ne riportano una sola. I modi con cui i valori della distribuzione normale sono pubblicati sono numerosi, ma tutti forniscono le stesse informazioni, permettono di derivare con facilità l’una dalle altre, servono per i medesimi scopi. In tutte quattro le tabelle riportate, il valore di z è fornito con la precisione di 2 cifre decimali. Nella prima colonna è riportato la quota intera con la prima cifra decimale; spesso il valore si ferma a 3,0 e quasi mai supera 4,0. Nella prima riga è riportato il secondo decimale, che ovviamente varia da 0 a 9 e spesso è indicato con 3 cifre da 0,00 a 0,09. Entro la tabella, all’incrocio del valore dato dalla somma della prima colonna con la prima riga, è riportata la quota di probabilità o frequenza relativa sottesa alla curva entro un intervallo prestabilito, stimato in modo differente nelle 4 tabelle.
La prima tabella riporta la quota dell’area in una coda della curva normale standardizzata, non importa se destra o sinistra. Il primo valore, collocato in alto a sinistra, è uguale a 0.500 e corrisponde ad un valore di Z uguale a 0.00. Significa che la quota di probabilità sottesa alla curva normale, a destra di un valore che si discosta dalla media m di una quantità pari a 0,00 s (quindi coincidente con la media stessa), è pari a 0.500 oppure 50% dei valori, se espresso in percentuale. In altri termini, i dati con valore superiore alla media sono il 50%. Per Z uguale a 1.00, la probabilità è 0.1587: significa che, considerando solo una coda della distribuzione, il 15,87 % dei dati ha un valore che si discosta dalla media di una quantità superiore a 1.00 volte s. I valori di Z usati con frequenza maggiore sono: - 1.645 perché delimita il 5% dei valori maggiori, - 1.96 per la probabilità del 2,5% sempre in una coda della distribuzione, - 2.328 per l’1%, - 2.575 per il 5 per mille.
La seconda tabella riporta l’area sottostante la distribuzione normale standardizzata nell’intervallo compreso tra la media m e il valore di Z. Considera le probabilità sottese in una coda della distribuzione, considerando la curva compresa tra la media e il valore che si discosta da essa di Z volte s. In termini molto semplici, è la differenza a .5000 della tabella precedente: mentre la prima tabella variava da .5000 a 0, questa varia simmetricamente da 0 a .5000. Per Z uguale a 0.00 è uguale a .0000, poiché nell’intervallo tra Z e Z + 0.00s non è compreso alcun valore. Per Z uguale a 1 è 0.3413. Considerando i valori di Z più frequentemente utilizzati, si hanno le seguenti relazioni: - 1.645 per il 45%, - 1.96 per il 47,5%, - 2.328 per il 49%, - 2.575 per il 49,5%.
La terza tabella fornisce la probabilità di ottenere un valore dello scarto standardizzato minore di Z. Poiché i valori inferiori alla media sono il 50%, parte da 0.5000 e tende a 1. Rispetto alla prima tabella, può essere visto come il complemento ad 1; rispetto alla seconda, ha aggiunto .5000 ad ogni valore. Per Z uguale a 0.00 è .5000, per Z uguale a 1.0 è uguale a 0.8413. Considerando i valori di Z più frequentemente utilizzati si hanno le seguenti relazioni: - 1.645 per il 95%, - 1.96 per il 97,5%, - 2.328 per il 99%, - 2.575 per il 99,5%.
La quarta tabella fornisce le probabilità nelle due code della distribuzione. Per ogni Z, il valore riportato è il doppio di quello della prima tabella. Parte da 1.000 e tende a 0 all’aumentare di z, con le seguenti relazioni: - 1.645 per il 10%, - 1.96 per il 5%, - 2.328 per il 2%, - 2.575 per l’1%.
Con una serie di esercizi, è possibile dimostrare in modo semplice e facilmente comprensibile l'utilizzazione pratica della distribuzione normale standardizzata. I calcoli utilizzano quasi esclusivamente la prima tabella, maggiormente diffusa nei testi di statistica applicata.
ESERCIZIO 1. Nella popolazione, la quantità della proteina A ha una media di 35 microgrammi e deviazione standard ( s ) uguale 5. Quale è la probabilità di trovare: a) individui con valori superiori a 40; b) individui con valori inferiori a 40; c) individui con valori inferiori a 25; d) individui con valori compresi tra 40 e 50; e) individui con valori tra 30 e 40.
Risposte: a) Con
Nella prima tabella a una coda, la probabilità esterna a Z = 1,00 è 0,1587; la frequenza di valori oltre 40 o la probabilità di trovare un valore oltre 40 è pari al 15,87%;
c) La probabilità di trovare individui con valori inferiori a 40 è 0,8413 (0,50000 prima della media e 0,3413 a Z = 1,00) corrispondente a 84,13%;
c) Con
Nella prima tabella a Z = -2,00 corrisponde un’area esclusa a sinistra della media pari 0,0228 cioè 2,28%.
d) Il valore di 40 e il valore 50 corrispondono rispettivamente a Z = 1,00 e a Z = 3,00. Nella prima tabella Z = 1,00 esclude il 15,87% delle misure mentre Z = 3,00 esclude il 0,01%; sono quindi compresi il 15,86%.
e) I due dati, 30 e 40 sono i valori compresi nell'intervallo Z = -1,00 e Z = +1,00; a sinistra e a destra della media l'area sottesa è in entrambi i casi pari a 0,3413 determinando un'area totale pari a 0,6826 (o 68,26%).
ESERCIZIO 2. E’ possibile utilizzare le tabelle anche nel modo inverso; cioè leggere su di esse la probabilità e ricavare il valore di Z corrispondente
a) Quale è il valore minimo del 5% dei valori maggiori? Nella prima tabella, la proporzione 0.05 non è riportata. Sono presenti - 0.051, che corrisponde a Z = 1,64 e - 0,049 che corrisponde a Z = 1,65. La loro media è 1,645. Essa indica che occorre spostarsi a destra della media (35) di una quantità pari a 1,645 volte la deviazione standard.
Il 5% dei valori più alti è oltre 43,225.
b) Quale è la quantità massima del 10% dei valori minori? Nella prima tabella, alla proporzione 0.100 corrisponde Z = 1,28. Essa indica che occorre spostarsi a sinistra della media (35) di una quantità pari a 1,28 volte la deviazione standard.
Il 10% dei valori più bassi è inferiore a 28,6.
ESERCIZIO 3. Un anestetico totale, somministrato prima di una operazione, ha una media di milligrammi 60 per Kg di peso, con una deviazione standard pari a 10. A dose superiori, con media uguale a 120 e deviazione standard 20, esso determina conseguenze gravi sulla salute del paziente.
a) Se un individuo vuole il 90% di probabilità di dormire, di quanto anestetico ha bisogno? Ma con quella quantità di anestetico con quale probabilità può avere conseguenze gravi?
Sempre dalla prima tabella, rileviamo che il valore che esclude la proporzione 0,100 a destra della distribuzione è Z = 1,28 . Pertanto da
ricaviamo che la quantità desiderata è 72,8 milligrammi per Kg di peso.
Per stimare il rischio che esso corre di avere conseguenze gravi, calcoliamo il valore di Z corrispondente alla seconda distribuzione normale
Nella tabella della distribuzione normale, a Z = 2,36 nella coda sinistra della distribuzione corrisponde una probabilità pari a 0,009. Se un paziente vuole la probabilità di dormire del 90% corre un rischio di avere conseguenze gravi pari al 9 per mille.
b) Ma il paziente ha molta paura e vuole il 99% di probabilità di dormire, di quanto anestetico ha bisogno? Ma con quella quantità di anestetico con quale probabilità può avere conseguenze gravi?
Sempre dalla prima tabella, rileviamo che il valore che esclude la proporzione 0,01 a destra della distribuzione è Z = 2,33 (ne compiono diversi, ma è la stima più precisa a due decimali). Pertanto da
ricaviamo che la quantità desiderata è 83,3 milligrammi per Kg di peso.
Per stimare il rischio che esso corre di avere conseguenze gravi, calcoliamo il valore di Z corrispondente alla seconda distribuzione normale
Nella tabella della distribuzione normale, a Z = 1,83 nella coda sinistra della distribuzione corrisponde una probabilità pari a 0,034. Se un paziente vuole la probabilità di dormire del 99% corre un rischio di avere conseguenze gravi pari al 34 per mille.
La statistica fa solo i calcoli, non decide. Deve farli bene, perché compete poi al paziente decidere, ma su dati corretti.
Oltre a quantificare la distribuzione dei valori intorno alla media della popolazione, la distribuzione normale serve anche per quantificare
la dispersione delle medie campionarie ( L’unica differenza rispetto a prima è che non si utilizza la deviazione standard, ma l’errore standard
che fornisce appunto la misura della dispersione delle medie di n dati, con frequenza prefissata :
Ad
esempio, entro quale intervallo si troverà il 95% delle medie campionarie di 10
dati ( Dopo aver rilevato nella tabella normale che per una probabilità a = 0.05 nelle due code della distribuzione è riportato Z = 1,96 da
si ricava che il 95% delle medie di 10 dati estratte da quella popolazione avrà - come limite superiore 33,72 - come limite inferiore 26,28.
2.4.4 APPROSSIMAZIONI E CORREZIONI PER LA CONTINUITA' Molte distribuzioni discrete, quali la binomiale, l'ipergeometrica e la normale, sono bene approssimate dalla distribuzione normale, per campioni sufficientemente grandi. L'uso della normale è giustificata anche dalla impossibilità pratica di effettuare i calcoli con le formule delle distribuzioni discrete, a causa di elevamenti a potenze alte e del calcolo di fattoriali per numeri grandi. Nonostante la corrispondenza dei risultati, tra distribuzioni discrete e distribuzioni continue esistono differenze nel calcolo delle probabilità. Le prime forniscono le probabilità per singoli valori della variabile casuale, cioè la probabilità di ottenere esattamente i volte un determinato evento; le seconde forniscono la probabilità cumulata da un certo valore fino all’estremo della distribuzione. Per calcolare la probabilità di un singolo valore, con la distribuzione normale si deve calcolare l'area sottesa all'intervallo X ± 0,5. In altri termini, per individuare un valore discreto i in una scala continua, occorre prendere non il valore esatto X ma l’intervallo unitario X ± 0,5.
ESEMPIO In una popolazione planctonica, la specie A ha una presenza del 10%; in un campionamento casuale di 120 individui quale è la probabilità di: a) trovarne esattamente 15 della specie A? b) trovarne almeno 15 della specie A? c) trovarne meno di 15 della specie A?
Risposte: (ricordando che n = 120; x = 15; µ = n×p = 120 x 0,10 = 12;
a ) Per stimare la probabilità di avere esattamente 15, che è un valore discreto, in una scala continua si deve calcolare la probabilità compresa nell’intervallo tra 14,5 e 15,5. Poiché la tabella della distribuzione normale fornisce la probabilità cumulata da quel punto verso l’estremo, il calcolo richiede 3 passaggi:
1- la stima della probabilità da 15,5 verso destra
corrispondente a µ
+ 1,06
2- la stima della probabilità da 14,5 verso l’estremo nella stessa direzione precedente:
corrispondente
a µ + 0,76
3 - la sottrazione della prima probabilità dalla seconda, per cui la probabilità di trovare esattamente 15 individui della specie A è 35,54 - 27,64 = 7,90% uguale a 7,9 %.
Con la distribuzione binomiale, per risolvere lo stesso esercizio il calcolo della probabilità avrebbe dovuto essere P(15) = che rappresenta un’operazione difficile da risolvere manualmente.
b) La probabilità di trovare almeno 15 individui della specie A potrebbe teoricamente essere calcolata con la distribuzione binomiale, sommando le singole probabilità esatte di trovare 15, 16, 17, ecc. fino a 120 individui. Alla precedente difficoltà di calcolo, si aggiunge quella del tempo richiesto per stimare queste 106 probabilità
da sommare per ottenere quella complessiva.
Con l'utilizzazione della distribuzione normale il calcolo diviene molto più semplice e rapido:
Si stima un valore della distribuzione normale standardizzata con z uguale a 0,76 equivalente ad una probabilità totale verso l’estremo uguale a 22,36%. Pertanto, la probabilità di trovare almeno 15 individui (15 o più individui) è uguale a 22,36%.
c) La probabilità di trovare meno di 15 individui, con la distribuzione binomiale è data dalla somma delle probabilità esatte di trovare da 0 a 14 individui:
Con la distribuzione normale il calcolo diviene:
Nella tavola della distribuzione normale standardizzata a Z = 0,76 corrisponde una probabilità, a partire dalla media, uguale a 27,64%. Ad essa va sommato 50 %, che corrisponde alla probabilità di trovare da 0 a 12 individui (la media). Pertanto, la probabilità complessiva di trovare meno di 15 individui è 50% + 27,64% = 77,64% uguale al 77,64%.
Allo stesso modo della distribuzione binomiale, è possibile approssimare la distribuzione ipergeometrica con la formula
dove: - N = numero totale di individui del campione, - n = numero di individui estratti dal campione.
Per la distribuzione di Poisson il calcolo del valore di z diviene
dove m è il valore della media che, come dimostrato, coincide con quello della varianza s2.
2.4.5 distribuzione rettangolare Come nelle distribuzioni discrete, anche tra le distribuzioni continue la più semplice è la distribuzione rettangolare, detta anche distribuzione uniforme continua. La distribuzione rettangolare continua, compresa nell'intervallo tra x1= a e x2 = b, come densità di frequenze relative ha la funzione
e pertanto è caratterizzata da una densità costante in tutto l'intervallo da a a b. Nella rappresentazione grafica questa distribuzione ha la forma di un rettangolo, figura che giustifica il suo nome. La media è
e la varianza
Ovviamente questa distribuzione è l'equivalente dell'uniforme discreta, considerata nel continuo.
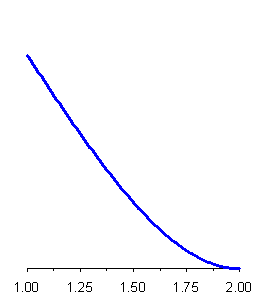
2.4.6 DISTRIBUZIONE ESPONENZIALE NEGATIVA La esponenziale negativa è una distribuzione continua con funzione
che prende il nome dall'esponente negativo che compare nella relazione. E' una funzione positiva o nulla continuamente decrescente, che tende a 0 per x che tende all'infinito. Nel discreto ha l'equivalente nella distribuzione geometrica decrescente. Media e varianza sono rispettivamente: media m
varianza s2
E' di estremo interesse pratico, per dedurre la curva sottostante una determinata distribuzione di dati sperimentali, notare che in questa distribuzione la varianza è uguale al quadrato della media.
2.4.7 LE CURVE DI PEARSON Karl Pearson ha proposto non una curva sola ma una famiglia di curve, utili per descrivere con elevata approssimazione molte distribuzioni empiriche, modificando i suoi parametri. Nonostante gli ottimi risultati ottenuti nell’approssimazione, ha il grave limite che i parametri che la definiscono non sono esplicativi del fenomeno e quindi si prestano male ad usi predittivi. La forma esplicita della funzione può essere espressa come
che dipende dalle radici dell'espressione quadratica del denominatore, cioè dai valori dei parametri b0, b1 e b2, e dove y e x sono i valori degli assi e c è una costante.
Il sistema gode della proprietà di rappresentare molte curve, come quelle di seguito disegnate.
Fig. 17. Curva di Pearson : forma a campana simmetrica Fig.18. Curva di Pearson: forma a U simmetrica
Variando i parametri prima definiti, si passa dall’una all’altra forma di curva.
Figura19. Curva di Pearson : forma a J rovesciato. Figura 20. Curva di Pearson : forma a J .
Anche la distribuzione normale e le sue approssimazioni, con curtosi ed asimmetria variabili, possono essere rappresentate come una delle possibili curve di Pearson.
Fig. 21 Curva di Pearson a campana asimmetrica Fig. 22 Curva di Pearson: forma a U asimmetrica.
Lo studio dettagliato delle diverse curve richiederebbe una trattazione complessa, che non viene affrontata in modo più dettagliato in questo corso, per le sue ridotte applicazioni nelle scienze ambientali ed ecologiche.
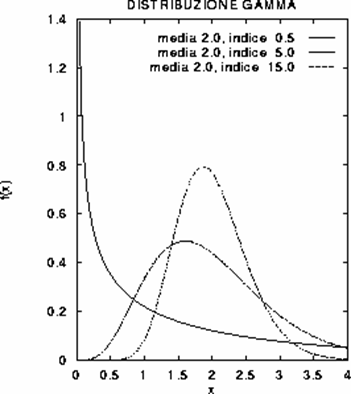
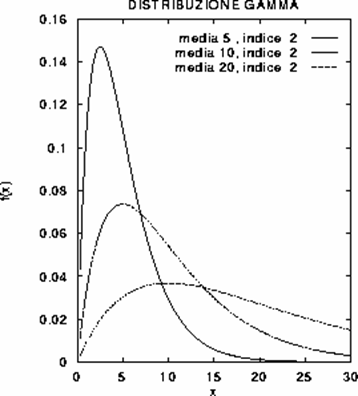
2.4.8 LA DISTRIBUZIONE GAMMA Un altro modello per descrivere la distribuzione di variabili casuali continue e positive, come altezza o lunghezza, peso, tempo, densità e concentrazione, è la distribuzione Gamma ( G ). La sua funzione di densità di probabilità è
f(x) = K × ( xn - 1 / mn ) exp (-nx / m) per x > 0 e dove sia m che n sono maggiori di 0, mentre K è una costante che rende unitaria l’area sottesa dalla curva. Quando x £ 0 la funzione è uguale a 0.
I parametri che determinano la funzione di densità della curva G ( indicata sui testi anche G da Gamma) sono - la media m ed n (chiamato indice della distribuzione), - mentre la costante K è data da K = nn/ G( n ), con G( n ) = ò0¥ x n-1 e - x dx
Per il calcolo di G(n) sono disponibili tavole apposite. Per n intero positivo, è possibile calcolare G(n) mediante G( n ) = ( n - 1) ! per i valori interi e G( n + ½ ) = Öp {(1 × 3 × 5 × 7 × ... × (2n-1)} / 2n per valori interi + 0,5.
I casi particolari più importanti della distribuzione Gamma sono - la distribuzione Esponenziale - la distribuzione Chi-quadrato ( c2 ).
Figura 22. Alcune distribuzioni Gamma
Figura 23. Altre forme della distribuzione Gamma.
La funzione di densità di probabilità della distribuzione esponenziale è f(x) = ( 1 / m ) exp ( - x / m) per x>0 dove m > 0.
La esponenziale è utile per descrivere la distribuzione delle durate di intervalli di tempo, in cui si manifesta un fenomeno biologico od ambientale, calcolando la distribuzione degli intervalli di tempo tra il manifestarsi di due eventi successivi. E’ in relazione con la distribuzione di Poisson, che fornisce la distribuzione degli eventi in un determinato intervallo di tempo. Se il numero di eventi i, che avvengono in un determinato intervallo di tempo t, segue la legge di Poisson con media l, - il tempo di attesa X intercorrente tra due eventi segue la legge esponenziale con parametro m = 1 / l.
Il tempo medio di attesa m tra due eventi è costante ed è pari al reciproco della media utilizzata nella distribuzione binomiale (in epidemiologia, chiamato tasso d’incidenza ed uguale al numero di nuovi eventi contati in un periodo unitario, come ora, giorno, mese, anno).
Figura 24. Distribuzione esponenziale (negativa).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Manuale di Statistica per la Ricerca e la Professione © Lamberto Soliani - Dipartimento di Scienze Ambientali, Università di Parma (apr 05 ed) ebook version by SixSigmaIn Team - © 2007 |