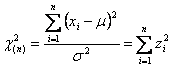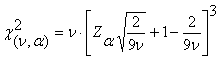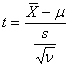DISTRIBUZIONI  e  leggi  di  probabilità'

 

 

 

2.5.   DISTRIBUZIONI CAMPIONARIE DERIVATE DALLA NORMALE ED UTILI PER L’INFERENZA

 

 

La distribuzione normale è valida per campioni molto numerosi, teoricamente infiniti. Spesso è possibile disporne nella statistica economica e sociale, in cui si analizzano i dati personali di una regione o una nazione. Nella pratica della ricerca statistica biologica, naturalistica ed ambientale, per l’inferenza sono disponibili alcune decine, al massimo poche centinaia di osservazioni. In molti settori della ricerca applicata, molto spesso i campioni hanno dimensioni ancora minori e la loro numerosità gioca un ruolo importante, nel determinare la forma della distribuzione. Essa non può più essere considerata normale od approssimativamente tale, ma se ne discosta quanto più il campione è piccolo.

Per l’inferenza, nella statistica parametrica l’ipotesi fondamentale è che questi campioni siano estratti da una popolazione normalmente distribuita. E’ un’ipotesi limitativa, ma basilare per le distribuzioni t di Student e F di Fisher, che insieme rappresentano le distribuzioni fondamentali dell’inferenza statistica parametrica. E’ importante comprendere come le 3 distribuzioni più utilizzate nell’inferenza statistica, la distribuzione c² di Pearson in quella non parametrica, la distribuzione t di Student e la F di Fisher, per la statistica parametrica, siano legate logicamente e matematicamente con la distribuzione normale e tra loro.

 

 

2.5.1   LA DISTRIBUZIONE c²

 

La distribuzione Chi-quadrato ( c² ), il cui uso è stato introdotto dallo statistico inglese Karl Pearson (1857–1936), può essere fatta derivare dalla distribuzione normale. Date n variabili casuali indipendenti x₁, x₂, …, x_n,

 normalmente distribuite con  m = 0  e  s = 1,

 il c² è una variabile casuale data dalla somma dei loro quadrati.

 

La funzione di densità di probabilità della distribuzione c²  è

f(x) = K × x  ^{(n / 2) - 1} exp (-x/2) 

 dove n = 1, 2, ...         e       K = 2 ^{- n / 2}  / G ( n / 2 ).

La funzione di densità del c² è determinata solo dal parametro n, il numero di gradi di libertà, pertanto viene scritta come c²_(n).

 

La distribuzione c²

parte da n uguale a 1 e al suo aumentare assume forme sempre diverse, fino ad una forma approssimativamente normale per n = 30

 

Una buona approssimazione è data dalla relazione

 

Con n molto grande (oltre 200,  per alcuni autori di testi) è possibile dimostrare che si ottiene una nuova variabile casuale (Z),  normalmente distribuita, con media m uguale a 0 e deviazione standard s uguale a 1

La distribuzione

chi quadrato e le sue relazioni con la normale possono essere spiegate in modo semplice attraverso alcuni passaggi.

Supponendo di avere una popolazione di valori X, distribuita in modo normale,

 

 la media m di questa distribuzione è

E(X) = m

 e la varianza s² è

E(X - m)² = s²

 

Se da questa distribuzione si estrae un valore X alla volta, per ogni singolo valore estratto si può stimare un punteggio Z² standardizzato attraverso la relazione

 

 

Questo valore al quadrato,  a differenza della Z,

- può essere solo positivo e variare da 0 all’infinito,

 

Esso coincide con il chi quadrato con un grado di libertà.

 

Nella distribuzione Z, il 68% dei valori è compreso nell’intervallo tra –1  e  +1; di conseguenza il chi quadrato con 1 gdl calcolato con

 

 ha una quantità equivalente di valori (il 68% appunto) tra 0 e 1.

 

Analizzando non un caso solo ma due casi, con la formula

 

    e   

 

si calcola un chi quadrato con 2 gradi di libertà

 

 

fondato su due osservazioni indipendenti, che avrà una forma meno asimmetrica del caso precedente e una quantità minore di valori compresi tra 0 e 1.

 

Con n osservazioni X_i indipendenti, estratte casualmente da una popolazione normale con media m e varianza s², si stima una variabile casuale chi quadrato

 

 

con n gradi di libertà e uguale alla somma degli n  valori Z².

 

Figura 25.  Alcune distribuzioni c²_(n), con gdl che variano da 1 a 10

 

La variabile casuale c²  gode della proprietà additiva: se due o più chi-quadrato, ognuno con i propri gdl sono indipendenti, dalla loro somma si ottiene un nuovo chi-quadrato con gdl uguale alla somma dei gdl.

 

Anche la varianza campionaria s² ha una distribuzione chi quadrato, come verrà in seguito approfondito. Il c² può servire per valutare se la varianza  di una popolazione, dalla quale sia stato estratto un campione con varianza S², sia uguale o diversa da un valore predeterminato. Questi concetti sono espressi nell’ipotesi nulla H₀

H₀:  =

con ipotesi alternativa H₁

H₁ =   ¹  

 

Per decidere alla probabilità a tra le due ipotesi, si stima un valore del chi quadrato

 

 

 determinato dal rapporto tra il prodotto degli n-1 gradi di libertà con il valore sperimentale s² e la varianza  attesa o predeterminata.

Per ogni grado di libertà, si dovrebbe avere una tabella dei valori del c²_(n), come già visto per la distribuzione normale. Per evitare di stampare tante pagine quante sono i gradi di libertà, di norma viene utilizzata una tavola sinottica, una pagina riassuntiva, che per ogni grado di libertà riporta solo i valori critici più importanti corrispondenti alla probabilità a del 5% (0.05), 1% (0.01), 5 per mille (0.005) e 1 per mille (0.001).

 

All’uso del c²_(n) è dedicato il successivo capitolo 3.

 

Non disponendo delle tabelle relative al chi quadrato e alla distribuzione normale, è possibile passare dall’una altra.

Per passare dai valori del c² al valore z, ricordando che, con n grande, la distribuzione c²_(n) è approssimativamente normale, è possibile ricorrere alla relazione

 

z_a =

 

poiché quando i gradi di libertà sono molto più di 100

la media m della distribuzione c²_(n) è uguale a n e

e la varianza s² è uguale a 2n.

 

Per esempio, si abbia con n =100, alla probabilità a = 0.05 il valore di c²= 124,342;

 mediante la relazione

 = 1,72

 

si ottiene un valore di z uguale a 1,72 mentre il valore corretto è 1,6449. L’errore relativo è del 4,5%.

 

Inversamente, dal valore di Z è possibile ricavare quello del c²_(n)  alla stessa probabilità a. Quando n è grande, maggiore di 100, per stimare il valore del chi quadrato che esclude una quota a di valori in una coda della distribuzione si ricorre alla relazione

 

 

in cui Z_a è il valore di Z alla probabilità a prefissata.

 

Per esempio, con n =100, alla probabilità a = 0.05 con il valore di Z = 1,6449 mediante la relazione

 

 = 124,056

 

 si calcola un valore di  uguale a 124,056 mentre il valore corretto alla terza cifra decimale, riportato nelle tabelle, è 124,342. Il processo inverso permette una stima migliore.

 

Una approssimazione ancora migliore, che fornisce una stima accurata anche con pochi gradi di libertà (n), è stata proposta da Wilson e Hilferty nel 1931 con la relazione

 

 

Per esempio, con n =10, alla probabilità a = 0.05 con il valore di Z = 1,6449 mediante la prima relazione, valida per n grande

 

 = 18,0048

 

si trova un valore di  uguale a 18,0048

mentre con la seconda relazione

 

 

 = 10 × 1,8297 = 18,297

 

 si trova un valore di   uguale a 18,297 che è molto più vicino al valore 18,3070 riportato nelle tabelle, appunto per  n =10, alla probabilità a = 0.05.

Nelle 2 tabelle successive, sono riporti i valori di z alle varie probabilità a per trovare il valore corrispondente del c² per i gradi di libertà n prefissati

(la tabella del chi quadrato è riportata alla fine del terzo capitolo).

 

a	0.995	0.990	0.975	0.950	0.900	0.750	0.500
Z	-2,5758	-2,3263	-1,9600	-1,6449	1,2816	-0,6745	0,0000

 

a	0.250	0.100	0.050	0.025	0.010	0.005	0.001
Z	+0,6745	+1,2816	+1,6449	+1,9600	+2,3263	+2,5758	+3,0902

 

Occorre ricordare che anche la distribuzione chi quadrato è normale, quando n è molto grande. Ciò spiega, in modo semplice ed intuitivo, perché in tale situazione quando Z è uguale a 0, alla probabilità a corrispondente al 50%, si abbia un valore del chi quadrato uguale alla sua media n.

La tabella dei valori critici mostra che con gradi di libertà n = 100, la media (corrispondente alla probabilità a = 0.500) non è esattamente 100 ma 99,3341 a dimostrazione del fatto che non è una distribuzione perfettamente normale.

 

 

2.5.2   LA DISTRIBUZIONE t DI STUDENT

 

La distribuzione t di Student (pseudonimo del chimico inglese Gosset che ne propose l’applicazione al confronto tra medie campionarie) considera le relazioni tra media e varianza, in campioni di piccole dimensioni, quando si utilizza la varianza del campione. La scelta tra l’uso della normale o della distribuzione t di Student nel confronto tra medie deriva appunto dalla conoscenza della varianza s² della popolazione o dal fatto che essa sia ignota e pertanto che, in sua vece, si debba utilizzare la varianza campionaria s².

Se una serie di medie campionarie () è tratta da una distribuzione normale ridotta (m = 0, s = 1) e la varianza del campione è s², con distribuzione c² e n gdl, è possibile derivare la v.c. t di Student, tramite la relazione

t² =

dove

 i gdl n corrispondono a N –1, con N uguale al numero totale di dati.

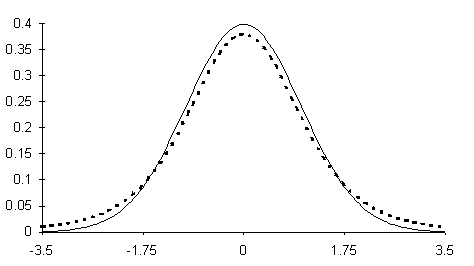
La curva corrispondente è simmetrica, leggermente più bassa della normale e con frequenze

 

maggiori agli estremi, quando il numero di gdl (n) è molto piccolo.

 

Per n che tende all’infinito, la curva tende alla normale.

 

 

Figura 26. Confronto tra la densità di probabilità della v.c. t di Student con gdl 5 (linea tratteggiata)

e la distribuzione normale corrispondente, con stessa media e stessa varianza (linea continua).

 

 

 

2.5.3   LA DISTRIBUZIONE  F  DI FISHER

 

Un’altra distribuzione di notevole interesse pratico, sulla quale è fondata l’inferenza di molta parte della statistica parametrica, è la distribuzione F.

Essa corrisponde alla distribuzione del

-  rapporto di 2 variabili casuali chi-quadrato indipendenti (A e B), divise per i rispettivi gradi di libertà (indicata da  e da ).

F = (A/m) / (B/n)

 

 

Questo rapporto F è definito tra 0  e  + ¥.

La curva dipende sia dal valore di n₁ e n₂, tenendo conto delle probabilità a.

Di conseguenza, in quanto definita da tre parametri, la distribuzione dei valori di F ha tre dimensioni.

Il problema della rappresentazione dei valori di F è risolto praticamente con 2-4 pagine sinottiche, che riportano solo i valori più utilizzati, quelli che fanno riferimento in particolare alle probabilità  0.05, 0.01 e, più raramente, 0.005 e 0.001.

 

L’ordine con il quale sono riportati i due numeri che indicano i gradi di libertà è importante: la densità della distribuzione F non è simmetrica rispetto ad essi. Per convenzione, le tavole sono calcolate per avere F uguale o maggiore di 1.

Per primo si riporta sempre il numero di gradi di libertà del numeratore, che è sempre la varianza maggiore, e per secondo quello del denominatore, che è sempre la varianza minore.

Il valore di F in teoria può quindi variare da 1 a +¥.

In realtà sono molto rari i casi in cui  supera 10; avviene solo quando i gradi di libertà sono pochi.

 

Storicamente,

-   la distribuzione F è stata proposta dopo la distribuzione t e ne rappresenta una generalizzazione.

Tra esse esistono rapporti precisi:

-  il quadrato di una variabile casuale t di Student con n gradi di libertà è uguale ad una distribuzione F di Fisher con gradi di libertà 1 e n.

 

t²_(n) = F_(1,n)    oppure    t_(n) =

 

E' una relazione che sarà richiamata diverse volte nel corso, in particolare quando si tratterà di passare dal confronto tra più medie al confronto tra solo due.

Inoltre il test t di Student permette confronti unilaterali più semplici ed immediati, che in molti casi sono vantaggiosi rispetto a quelli bilaterali. Anche questi concett saranno sviluppati nella presentazione dei test d'inferenza.

Aree in una coda della curva normale standardizzata

 

             

 

La tabella riporta la probabilità nell’area annerita

 

 

Z	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0.500	0.496	0.492	0.488	0.484	0.480	0.476	0.472	0.468	0.464
0,1	0.460	0.456	0.452	0.448	0.444	0.440	0.436	0.433	0.429	0.425
0,2	0.421	0.417	0.413	0.409	0.405	0.401	0.397	0.394	0.390	0.386
0,3	0.382	0.378	0.374	0.371	0.367	0.363	0.359	0.356	0.352	0.348
0,4	0.345	0.341	0.337	0.334	0.330	0.326	0.323	0.319	0.316	0.312
0,5	0.309	0.305	0.302	0.298	0.295	0.291	0.288	0.284	0.281	0.278
0,6	0.274	0.271	0.268	0.264	0.261	0.258	0.255	0.251	0.248	0.245
0,7	0.242	0.239	0.236	0.233	0.230	0.227	0.224'	0.221	0.218	0.215
0,8	0.212	0.209	0.206	0.203	0.200	0.198	0.195	0.192	0.189	0.187
0,9	0.184	0.181	0.179	0.176	0.174	0.171	0.169	0.166	0.164	0.161
1,0	0.159	0.156	0.154	0.152	0.149	0.147	0.145	0.142	0.140	0.138
1,1	0.136	0.133	0.131	0.129	0.127	0.125	0.123	0.121	0.119	0.117
1,2	0.115	0.113	0.111	0.109	0.107	0.106	0.104	0.102	0.100	0.099
1,3	0.097	0.095	0.093	0.092	0.090	0.089	0.087	0.085	0.084	0.082
1,4	0.081	0.079	0.078	0.076	0.075	0.074	0.072	0.071	0.069	0.068
1,5	0.067	0.066	0.064	0.063	0.062	0.061	0.059	0.058	0.057	0.056
1,6	0.055	0.054	0.053	0.052	0.051	0.049	0.048	0.048	0.046	0.046
1,7	0.045	0.044	0.043	0.042	0.041	0.040	0.039	0.038	0.037	0.037
1,8	0.036	0.035	0.034	0.034	0.033	0.032	0.031	0.030	0.029	0.029
1,9	0.029	0.028	0.027	0.027	0.026	0.026	0.025	0.024	0.024	0.023
2,0	0.023	0.022	0.022	0.021	0.021	0.020	0.020	0.019	0.019	0.018
2,1	0.018	0.017	0.017	0.017	0.016	0.016	0.015	0.015	0.015	0.014
2,2	0.014	0.014	0.013	0.013	0.013	0.012	0.012	0.012	0.011	0.011
2,3	0.011	0.010	0.010	0.010	0.010	0.009	0.009	0.009	0.009	0.008
2,4	0.008	0.008	0.008	0.008	0.007	0.007	0.007	0.007	0.007	0.006
2,5	0.006	0.006	0.006	0.006	0.006	0.005	0.005	0.005	0.005	0.005
2,6	0.005	0.005	0.004	0.004	0.004	0.004	0.004	0.004	0.004	0.004
2,7	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003	0.003
2,8	0.003	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.002
2,9	0.002	0.002	0.002	0.002	0.002	0.002	0.002	0.001	0.001	0.001
3,0	0.001

 

Valori della distribuzione normale standardizzata.

 

           

 

La parte annerita rappresenta l’area sottostante la distribuzione normale standardizzata dalla media aritmetica a z.

 

 

 

 

 

Valori dell’integrale di probabilità della distribuzione normale standardizzata

 

L’area annerita rappresenta la probabilità di ottenere un valore dello scarto standardizzato minore di z.

 

 

 

 

 

 

Area nelle due code della distribuzione normale standardizzata

 

La tabella riporta le probabilità nelle aree annerite.