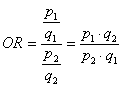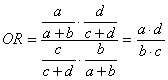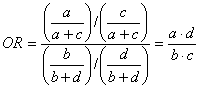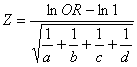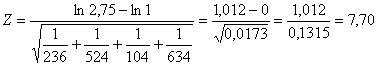COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

 

20.11.   ODDS RATIO E CROSS PRODUCT RATIO; INTERVALLO DI CONFIDENZA; TEST DI SIGNIFICATIVITA’ PER UNO E TRA DUE ODDS RATIO

 

 

Il rischio relativo (relative risk = p₁/p₂), come presentato nel paragrafo precedente, è espresso dal rapporto della probabilità tra persone esposte (p₁) al rischio e quella di persone non esposte (p₂).

E’ un metodo facile da capire; ma ha il grave svantaggio di essere costruito sul denominatore. Se la proporzione del rischio per i non esposti è piccola, il rapporto diventa grande ma con una misura approssimata. Se tale proporzione è grande, vicina a 1come quella delle persone esposte, anche il valore di RR tende a 1.

 

Ad esempio:

-  se p₂ = 0,6 (ovviamente rispetto a p₁), il valore del rischio relativo è 1/0,6 = 1,67

-  se p₂ = 0,9 (sempre rispetto a p₁ e minore di esso perché rappresenta il rischio delle persone non esposte), il valore del rischio relativo è 1/0,9 = 1,11.

Per superare questo limite, le due proporzioni sono stabilizzate attraverso la relazione

 

Quindi il rapporto tra le due proporzioni p₁ e p₂ diventa il rapporto di probabilità o

 odds ratio (OR):

Odds ratio è un termine tecnico inglese, che nei testi di statistica in italiano spesso non è tradotto; significa rapporto di probabilità.

 

Se p è la probabilità di un evento, l’odds è la probabilità a favore del successo,

(If two proportions p₁, p₂ are considered and the odds in favor of success are computed for each proportions, then the ratio of odds, or odds ratio, becomes a useful measure for relating the two proportions).

 

In una tabella di contingenza 2 x 2

 

 

 

 

 con

p₁ =        q₁ =         p₂ =           q₂ =

 l’odds ratio diventa

 

E’ il prodotto incrociato o Cross Product Ratio, abbreviato spesso in CPR.

 

Quando si parla di ammalati presenti in un gruppo di persone esposte (caso) rispetto agli ammalati in un gruppo di non esposti (controllo) si ha il disease odds ratio (OR), definito come la probabilità di essere colpiti dalla malattia per il gruppo di esposti, diviso la probabilità del gruppo dei non esposti.

 

A volte è possibile che, trattandosi di conteggi, una o più delle 4 caselle (a, b, c, d) siano uguali a 0. Ne deriva che il valore di OR, calcolato sul prodotto incrociato, diventa indeterminato.

 

In tal caso, se almeno una frequenza è pari a 0,

OR è dato da

OR =

 

ESEMPIO 1 (stessi dati del paragrafo precedente).  Su un campione di 4 mila persone che giornalmente assumono il farmaco X, 11 presentano i sintomi della malattia A. Nel campione di controllo, formato da 10 mila persone, gli individui affetti sono 7.

Calcolare il desease odds ratio (OR).

 

Risposta. Utilizzando la formula

 con

-  p₁ = 11/4000 = 0,00275      e     q₁ = 1 – 0,00275 = 0,99725

-  p₂ = 7/10000 = 0,00070     e      q₂ = 1 – 0,00070 = 0,9993

 si ottiene

 

 con un risultato approssimato, in funzione del numero di decimali utilizzati nelle proporzioni.

Impostato come una tabella 2 x 2 con le frequenze assolute

 

 

 

si ottiene

 lo stesso identico risultato.

Ma con una stima che è più semplice della precedente.

Quando, come in questo caso che rappresenta la norma, il valore è maggiore di 1, l’interpretazione è che il gruppo degli esposti ha  una probabilità maggiore di essere colpito dalla malattia di quello dei non esposti al rischio. Nel caso di  OR,

-  quando p₁ ha un valore prossimo a 0, anche OR tende a 0.

-  quando p₁ ha un valore prossimo a 1, OR tende a infinito.

 

E’  possibile valutare anche l’exposure odds ratio, definito come il rapporto (ratio) tra la probabilità (odds) di un ammalato di essere del gruppo degli esposti e la probabilità di essere stato tra i non esposti.

 

In una tabella di contingenza 2 x 2

 

 

 

 

 l’exposure odds ratio diventa

 

 uguale all’odds ratio e al disease odds ratio.

 

Come evidenziato per il rapporto tra rischi (RR), anche l’odds ratio (OR) è un rapporto e quindi la sua distribuzione campionaria ha una forte asimmetria destra. Di conseguenza, la varianza è stimata attraverso la trasformazione logaritmica. Per il suo calcolo, sono stati proposti molti metodi.

 

Tra i più semplici e diffusi è da ricordare il metodo di Woolf, proposto appunto da B. Woolf nel 1955 in una ricerca per confrontare il rischio di malattie nei vari gruppi sanguigni (con l’articolo On estimating the relation between blood group and disease, pubblicato su Annals of Human Genetics, Vol. 19, pp. 251-253)

 

La varianza dell’odds ratio è

 

La sua radice quadrata, quindi la deviazione standard, in realtà

è l’errore standard (se = standard error)

 

Assumendo che la distribuzione del ln(OR) sia approssimativamente normale, alla probabilità a l’intervallo di confidenza è

 

Anche per la varianza e l’errore standard dell’odds ratio è possibile che, trattandosi di conteggi, una o più delle 4 caselle (a, b, c, d) siano uguali a 0.

Ne deriva che il valore di OR e il suo errore standard diventano infiniti.

In tal caso, quando almeno una frequenza è pari a 0,

 l’errore standard es_(lnOR) è

es_(lnOR) =

 

Secondo quanto proposto da M. Pagano e K. Gauvreau nel 1993 nel loro testo Principles of biostatistics (Belmont, CA, Duxbury Press), questo metodo sarebbe da utilizzare anche come correzione per la continuità, quando il campione è piccolo.

 

Per stimare l’intervallo fiduciale di OR, si deve

-  trasformare il suo valore in lnOR,

-  calcolare l’intervallo fiduciale alla probabilità a prefissata,

 che per (1 - a) = 0,95  e quindi Z = 1,96 è

lnOR ± 1,96 x es_(lnOR)

 

- riconvertire i ln dei due valori estremi l₁ e l₂ dell’intervallo fiduciale in OR, mediante elevamento a potenza di   cioè di  2,71828^l

 

 

ESEMPIO 1.  Si vuole verificare se in una popolazione anziana, che da vari anni risiede in una zona ad alto inquinamento, le malattie polmonari hanno un’incidenza maggiore rispetto a quella della popolazione di pari età che risiede in una zona con inquinamento basso. La raccolta dei dati ha fornito i seguenti risultati

 

 

 

 

Stimare alla probabilità 1 - a = 0,95 l’intervallo di confidenza del rischio relativo di malattie polmonari, per la popolazione che da anni risiede nella zona ad alto inquinamento.

 

Risposta.  Il rapporto incrociato o odds ratio (OR)

 tra le popolazioni che vivono nelle due zone diverse

 è

OR =  =  = 2,75

 uguale a 2,75.

Esso sta ad indicare che la frequenza relativa delle persone con malattie polmonari nella zona ad alto inquinamento è 2,75 volte più elevato di quella presente nella zona a basso inquinamento.

 

Di questa stima media è possibile calcolare l’intervallo di confidenza.

 

A questo scopo, si ricorre al suo logaritmo naturale

lnOR = ln 2,75  = 1,012

 e se ne stima l’errore standard

es_(lnOR)  =  

es_(lnOR)=   = 0,1315

 

 che, sempre espresso in logaritmo naturale, risulta es_(lnOR) = 0,1315.

 

L’intervallo di confidenza deve dapprima essere calcolato per il ln (cioè per lnOR) e successivamente essere riportato al valore del rapporto reale.

Con i dati dell’esempio,

 alla probabilità 1- a = 0,95 il ln dell’intervallo di confidenza di OR

ln OR  =  1,012  ±  1,96  x  0,1315  = 1,012 ± 0,258

 risulta compreso tra 0,754 e 1,270.

Di conseguenza, alla probabilità 1- a = 0,95 il valore reale del rapporto OR, cioè il rischio relativo o rapporto tra rischi per le persone che risiedono in una zona ad alto inquinamento rispetto a quelli che risiedono in una zona a basso inquinamento (risultato uguale a 2,75), con questi dati campionari è compreso tra i due limiti

- l₁ =  =  2,71828^0,754  = 2,13

- l₂ =  = 2,71828^1,270  = 3,56.

E’ chiaramente una distribuzione non simmetrica, con asimmetria destra.

 

ESEMPIO  2. (tratto, con elaborazione, dal testo di Bernard Rosner (2000) Fundamentals of Biostatistics, 5^th ed. Duxbury). Stimare il risk ratio e il suo intervallo di confidenza alla probabilità del 95%, per il cancro al seno in donne che hanno avuto il primo figlio all’età di almeno trenta anni rispetto a donne che lo hanno avuto prima dei 30 anni, con i seguenti dati

 

 

Risposta.  Dalla tabella risulta che

-  per le donne che hanno avuto il primo figlio più giovani (età £ 29 anni), la frequenza relativa o proporzione di ammalate di cancro al seno è  p = 1498 / 10245 = 0,146

-  per le donne che hanno avuto il primo figlio in età più avanzata (età ³ 30 anni), la frequenza relativa o proporzione è  p = 683 / 3220 = 0,212.

Una prima osservazione è che non è richiesto che i due campioni abbiano lo stesso numero di osservazioni; anzi è meglio che il campione con la frequenza minore sia più ampio, come nell’esempio.

La seconda osservazione è che, per calcolare il rischio relativo, la tabella deve essere impostata in modo tale che il campione con il rischio maggiore sia nella prima riga.

La tabella precedente diventa

 

 

 

 

In essa l’odds ratio o risk ratio è

 uguale a 1,572

Il suo intervallo di confidenza è dato da

 

Per la probabilità a = 0.05 e quindi con Z = 1,96 e con i dati dell’esempio,

 diventa

 

 

 

 e determina

-  il limite inferiore l₁ = 0,452 – 0,101 = 0,351

-  il limite superiore l₂ = 0,452 + 0,101 = 0,553

Si ritorna alla scala del rapporto con l’antilog ( dove ):

-  il limite inferiore è l₁ =  =   = 1,42

-  il limite superiore è l₂ =  =   = 1,74

In conclusione si può affermare che il rischio relativo per le donne che hanno avuto il primo figlio ad età più alta è 1,57 rispetto a quelle che lo hanno avuto prima dei 30 anni. Alla probabilità del 95%, tale rischio è compreso tra 1,42 e 1,74.

 

Su principi simili è fondata, con un test che può essere sia bilaterale sia unilaterale, la significatività dell’odds ratio, cioè  la verifica dell’ipotesi nulla che l’odds ratio sia significativamente maggiore di 1. La procedura è basata su gli stessi concetti dell’intervallo di confidenza appena illustrati, come mostrano R. Christensen nel 1990 (nel volume Log-linar models, edito da Springer-Verlag, New York) e M. Pagano e K. Gauvreau nel loro lavoro del 1993 (vedi il testo Principles of biostatistics, edito da Duxbury Press, Belmont CA).

Anche in questo caso, si ricorre alla trasformazione logaritmica (ln) sulla base di due considerazioni:

- se è vera l’ipotesi nulla H₀

p₁ = p₂

 si  ha  OR = 1; quindi il rapporto tra le due probabilità (quella dell’effetto del farmaco rispetto al controllo o della zona ad alto inquinamento rispetto a quella a basso inquinamento) è uguale a 1 e il ln di 1 è uguale a 0;

-   tradotte per OR, le ipotesi del test unilaterale di significatività diventano

H₀: OR £ 1     contro    H₁: OR > 1

 

La significatività è quindi determinata attraverso

 la distribuzione  Z

 

ESEMPIO 3. Con gli stessi dati dell’esempio 1, valutare se l’odds ratio delle persone con malattie polmonari è significativamente maggiore di 1, come atteso nel confronto tra persone che vivono in una zona ad alto inquinamento rispetto a quelle che vivono in un’area a basso inquinamento

 

 

 

 

Risposta. Per verificare l’ipotesi unilaterale

H₀: OR £ 1      contro      H₁: OR > 1

 si può utilizzare la distribuzione Z

Pertanto, dopo aver ricavato

OR =  =  = 2,75

 OR uguale a 2,75 si calcola

 

 il valore Z = 7,70. E’ talmente alto da essere significativo con probabilità inferiore a circa 1 su un milione.

Quasi sempre questo test è unilaterale, per cui il valore critico di confronto per

-   a = 0.05  è  Z = 1,646

-   a = 0.01  è  Z = 2,33

Quando il test è bilaterale, per cui a priori è atteso che l’odds ratio possa risultare inferiore oppure superiore a 1, il valore critico di confronto per

-   a = 0.05  è  Z = 1,96

-   a = 0.01  è  Z = 2,58.

 

E’ possibile anche il confronto tra due odds ratio, ovviamente calcolati in modo indipendente, cioè mediante due differenti tabelle 2 x 2.

Il test può essere sia bilaterale che unilaterale, utilizzando la distribuzione Z,

dopo aver calcolato

 

ESEMPIO 4. Si ritiene che l’odds ratio tra persone che vivono in zone ad alto inquinamento e persone che vivono in aree a basso inquinamento sia maggiore per gli anziani rispetto ai giovani.

In una popolazione è quindi stato accertato il numero di persone risultate affette da malattie polmonari, separando gli anziani dai giovani. La distribuzione ottenuta nelle due tabelle di contingenza

 

 

 

 

 è in accordo con l’atteso?

 

Risposta.  E’ un test unilaterale. Indicando con OR₁ l’odds ratio degli anziani e con OR₂ quello dei giovani, l’ipotesi da verificare è

H₀: OR₁ £ OR₂      contro      H₁: OR₁ > OR₂

Dopo aver stimato

- l’odds ratio degli anziani

 e la sua varianza

 

- l’odds ratio dei giovani

 e la sua varianza

 

- si calcola il valore di Z

 che risulta Z = 2,05.

Nella distribuzione normale unilaterale, a Z = 2,05 corrisponde una probabilità P = 0,02 che permette di rifiutare l’ipotesi nulla. Con i due campioni raccolti, si conferma che l’odds ratio degli anziani è significativamente maggiore di quello dei giovani.