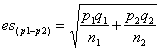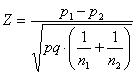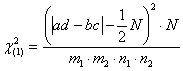COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

20.1.  I PRIMI ANNI DEL CHI- QUADRATO: CENNI SU NASCITA ED EVOLUZIONE

 

 

Le misure di associazione sono fondate sul valore del , ricavato da una tabella di contingenza di dimensioni minime  2 x 2 oppure di dimensioni generiche r x c. Anche la loro significatività è verificata attraverso questo test:

- un valore di associazione è significativo, se lo è il  calcolato sulla stessa tabella di dati.

E’ quindi fondamentale una conoscenza approfondita delle sue origini e delle sue caratteristiche distintive del , anche per impostare correttamente e meglio comprendere le misure di associazione - indipendenza tra due variabili. Questi argomenti sono illustrati nei paragrafi successivi.

 

Per questa rilettura storica e di approfondimento dei metodi già presentati nei capitoli iniziali, sono di aiuto due pubblicazioni scientifiche internazionali:

1 -  l’articolo di Frank Yates (1902-1994, già assistente di Fisher nel 1931 presso l’Istituto di ricerche agrarie Rothamsted di Londra) del 1984 intitolato  Test of Significance for 2 x 2 Contingency Tables (su Journal of the Royal Statistical Society, A, Vol. 147, Part.3, pp.: 426-463), nel quale sono presentate le idee originarie su cui è stato impostato il test di significatività per tabelle di contingenza 2 x 2; questo articolo è stato pubblicato a 50 anni esatti di distanza dal suo articolo del 1934, il famoso Contingency tables involving small numbers and the  test (pubblicato su Journal of the Royal Statistical Society, Suppl., 1, pp.: 217-235), con cui Yates propose la correzione per la continuità che ha preso il suo nome, e ne rappresenta una difesa scientifica importante;

- la rassegna sull’evoluzione di questi metodi scritta da Noel Cressie e Timothy R. C. Read nel 1989 Pearson’s X² and the Loglikelihood Ratio Statistic G²: A Comparative Review (pubblicata su International Statistical Review Vol. 57, 1, pp.: 19-43).

 

Nel paragrafo che intitola Early History, F. Yates inizia la sua rassegna dell’evoluzione dei concetti dalla proposta originaria formulata da Karl Pearson (1857-1936) nel 1900, per applicare test sulla bontà dell’adattamento (test for goodness of fit). La nascita del  è individuata nell’articolo On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling (pubblicato su Philosophical Magazine, 5^th  Series, Vol. 50, pp.: 157-172).

 

Questo test è proposto per

- confrontare un gruppo di frequenze osservate in un esperimento con un gruppo di frequenze attese, che sono stimate sulla base di un modello  indipendente dai dati raccolti.

 

Le frequenze possono essere

-  sia il risultato del raggruppamento di dati continui in categorie,

-  sia il conteggio di dati originariamente qualitativi, come avviene nelle tabelle di contingenza.

 

E’ l’utilizzazione più semplice di . Come definito da Pearson, il metodo

 è fondato sulla relazione

 dove

- X =  è un vettore random di frequenze, con

-    e   E(X) =

-  e dove  p =  è un vettore di probabilità con  .

 

Sempre nell’articolo di Karl Pearson del 1900,

- la distribuzione asintotica di X² è fornita dal  con gradi di libertà uguali a  , quando le probabilità  sono numeri noti a priori e derivati da una legge esterna, cioè non sono ricavati dalla distribuzione campionaria delle frequenze raccolte.

Questa corrispondenza asintotica tra  e  richiede che

-  le frequenze attese siano infinite in tutte le celle.

 

E’ una assunzione teorica, soddisfatta in pratica quando

- ogni frequenza attesa () è ³ 5,

 poiché la formula del X² è derivata da una distribuzione poissoniana, in cui la probabilità  tende a 0 (zero) e quindi  deve essere grande.

 

Karl Pearson affermò anche che, quando le probabilità  dipendono dai parametri che è necessario stimare, vale a dire che sono ricavate dalla distribuzione campionaria,

- per un test d’inferenza è ancora adeguato il  con  gradi di libertà.

Tale affermazione, seguita per circa vent’anni,  sollevò un’ampia discussione.

La soluzione corretta è stata proposta solamente nel 1924 da Ronald Aylmer Fisher (1890-1962) con l’articolo The conditions under which  measures the discrepancy between observation and hypothesis (pubblicato su Journal of the Royal Statistical Society, Vol. 87,  pp.: 442-450).

In una tabella r x c, le frequenze attese sono ricavate dai totali delle frequenze osservate. Pertanto

- i gradi di libertà sono , dove  è il numero di parametri stimati mediante i dati campionari.

 

In una tabella di contingenza 2 x 2  (ricordando che per convenzione   e  )

 con la simbologia classica

 

 

 

 

 i gradi di libertà sono  = 1.

Infatti, in questo metodo condizionale proposto da Fisher,

-  i totali  e  sono necessari per calcolare la frequenza attesa di ,

-  che rappresenta l’unico dato atteso che è effettivamente libero di assumere qualsiasi valore.

 

La generalizzazione di questo concetto porta al fatto che  in una tabella  

-  i gradi di libertà sono ,

-  non .

L’errore di Pearson diventava particolarmente grave in una tabella 2 x 2, poiché

-  il  ha un solo grado di libertà e non tre.

 

Nel 1911, pochi anni dopo l’articolo di Pearson del 1900, George Udny Yule (1871-1951) propone un test per l’associazione in tabelle di contigenza 2 x 2, con il volume Introduction to the Theory of Statistics (London, Griffin). In campioni grandi, si può utilizzare

-  la stima dell’errore standard, che per una proporzione  in un campione di  dati

 è

 

Per una differenza campionaria o osservata  

 dove    e   ,

 l’errore standard diventa

 

Se tra le frequenze relative  e  non esiste una differenza significativa, entrambe possono esser sostituite dalla loro stima combinata ,  dove

Con questa stima combinata, come dimostrato nel capitolo sul chi-quadrato,

 il risultato del test di Yule

 

-  è equivalente al test  di Pearson con un grado di libertà:

In realtà, nel suo testo Yule non fa menzione di questa corrispondenza. Presumibilmente perché al test  di Pearson venivano ancora attribuiti 3 gradi di libertà.

 

 Per il calcolo  di Pearson in una tabella 2 x 2 , la formula abbreviata più conveniente e nota

 è

 

Sulla base di concetti uguali e metodi analoghi a quelli che porteranno alcuni decenni dopo alle tecniche Monte Carlo e a quelle di ricampionamento, allo scopo di effettuare una verifica empirica dei modelli matematici della distribuzione , nel 1915 M. Greenwood e G. U. Yule nell’articolo The statistics of anti-cholera and anti-typhoid inoculations, and the interpretation of such statistics in general (pubblicato da Proc. R. Soc. Med. (Epidemiology), Vol. 8, pp.:113-190) costruiscono 350 tabelle 2 x 2  e 100 tabelle 4 x 4, ottenendo una distribuzione che di fatto è indipendente dal modello teorico.

I risultati empirici coincidono con quelli del modello, ma con una stima diversa da quella proposta da Pearson per i gradi di libertà. Tuttavia Greenwood e Yule non pubblicarono questi risultati.

E’ R. A. Fisher che nel 1922, con l’articolo On the interpretation of  from contigency tables, and the calculation (su Journal of the Royal Statistical Society, Vol. 85,  pp.: 87-94), solleva esplicitamente il problema dell’errore di Pearson nel calcolo dei gradi di libertà. Questi non ammette la presenza di un errore e nasce una controversia accesa.

Ora, da decenni, è universalmente accettata la correttezza dell’impostazione di Fisher.

 

Mentre con campioni grandi la proposta di Udry di approssimazione alla normale è universalmente accettata, con campioni piccoli il problema è più complesso e controverso.

Il metodo più diffuso è dovuto a R. A. Fisher, proposto nel suo testo del 1925 Statistical Methods for Research Workers. E’ un metodo esatto, che fornisce direttamente la probabilità della risposta sperimentale e di ogni altra risposta possibile. E’ fondato sul fatto che i totali marginali sono inclusi nella valutazione delle probabilità: si tratta di una restrizione (definita in termini tecnici ipotesi condizionale) che è implicita nel calcolo del  con tabelle, dove la frequenza attesa in ogni singola cella è calcolata a partire dai totali marginali delle frequenze osservate (come illustrato nel capitolo 3).

Nel 1934 Yates dimostra che la distribuzione del valore del  è fortemente migliorata quando la differenza tra osservato e atteso è ridotta di 0,5 che egli chiama correzione per la continuità. (Nell’articolo già citato del 1984 scrive: This I termed the continuity correction).

In tabelle 2 x 2, la formula abbreviata più conveniente

 diventa

 

 Fornisce un risultato del tutto corrispondente al sottrarre 0,5 alla differenza tra osservato e atteso in ogni casella.

 

Mentre il metodo esatto è un test essenzialmente a una coda, in quanto permette di stimare la probabilità del singolo evento e di sommarlo poi con tutti gli eventi più estremi nella stessa direzione,

il  è essenzialmente un test a due code. Si ricava la probabilità  per un test a una coda, prendendo la metà della probabilità ottenuta con il test.

Lo stesso concetto è valido per la posto di Udry sul confronto tra due proporzioni con la distribuzione Z, che può essere sia unilaterale che bilaterale.

 

Nell’articolo del 1984, tra le altre  Yates fornisce due risposte interessanti in merito alle controversie sul chi quadrato. Le critiche riguardavano in particolare due aspetti

1 -  l’uso dell’approccio condizionale in tabelle 2 x 2, poiché secondo alcuni statistici è logico nella stima delle frequenze attese mantenere costante le dimensioni dei due campioni, ma è poco convincente mantenere costante anche la proporzione ,  che rappresenta la proporzione di successi campionari di quell’esperimento;

2 - le probabilità  ottenute con il metodo esatto di Fisher e con il  quando è applicata la correzione per la continuità di Yates forniscono risposte uguali,  ma con valori maggiori di quelle del  di Pearson; quindi, permettono di rifiutare l’ipotesi nulla più raramente.

 

Yates risponde:

1 -  L’uso dei totali marginali ricavati dalla distribuzione osservata per calcolare i valori attesi  è una restrizione che di fatto è implicita già nel test  di Pearson: This was suggested to me by Fisher, and depends on the restriction that only sets of values conforming to both pairs of observed marginal totals are included in evaluating the probabilities, a restriction wich is in fact also implicit in the  test, as the expectations of the cell values are calculated from the marginal totals (pag. 429, righe 5-9).

2 - L’uso di livelli nominali convenzionali di significatività come il 5 e 1 per cento, quando i dati sono discontinui, deve essere attuato con buon senso. Il simbolismo matematico adottato dalla scuola di Neyman-Pearson

    ,   

 o quello ancora più assurdo, se  può essere negativo,

    ,   

 ha incoraggiato l’uso di livelli nominali che può essere gravemente fuorviante con dati discreti. With discontinous data, the use of nominal levels can be seriously misleading (p. 435, terza riga dal fondo).

Esemplifica questo concetto evidenziando che se si lancia una moneta 10 volte,

 -  la probabilità di trovare 9 volte oppure 10 volte testa ha una probabilità di 1,1 per cento,

 -  la probabilità di trovare 8 o più volte testa ha una probabilità del 5,5 per cento.

Non esiste alcun  motivo per confrontare tali probabilità con quelle riportate su una scala continua di 1,0 e 5,0 per cento. E’ più corretto ragionare e decidere sulla base di queste probabilità che sono state ricavate: The actual significance probability attained should therefore always be given when reporting on discontinous data (pag. 437, seconda riga).

 

E’ di particolare importanza questa seconda osservazione, che è estensibile a tutta la statistica non parametrica nel caso di piccoli campioni. Inoltre assume una rilevanza generale, per l’interpretazione da fornire quando la probabilità  calcolata è vicina ai valori critici:

- superare o meno il valore critico prefissato per quantità minime non è un fattore distintivo rilevante, per la significatività del risultato.