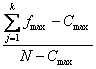COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

20.6.   ASSOCIAZIONE PER VARIABILI CATEGORIALI IN TABELLE r x c: LA PRE,  IL l simmetrico ed asimmetrico di Goodman e Kruskal, CENNI SU la UC O U di theil

 

 

Le tabelle r x c sono costruite per tre grandi tipi di variabili: nominali, ordinali e intervallari:

-  nel primo caso, cioè con variabili nominali, si parla di associazione (gli indici sono presentati in questo paragrafo); 

-  nel secondo caso, cioè con variabili di tipo ordinale, si parla di cograduazione (gli indici verranno presentati nel paragrafo successivo);

-  nell’ultimo caso, quando le variabili sono misurate su una scala ad intervalli o di rapporti, la relazione tra le due variabili è chiamata correlazione (gli indici sono già stati presentati sia nella forma parametrica sia in quella non parametrica).

 

I risultati ottenuti con i metodi precedenti, tutti fondati sul , restano difficili da interpretare, anche dopo le trasformazioni proposte, cioè mediante indici che tengono in considerazione la numerosità del campione e le dimensioni della tabella. In particolare quando i valori sono distanti da zero e quindi non si ha indipendenza tra le due variabili qualitative, non è chiaro il tipo di associazione. Per renderlo più evidente, nel 1954 Leo A. Goodman e E. H. Kruskal hanno introdotto il concetto di Riduzione Proporzionale nell’Errore, abbreviato in PRE da Proportionate Reduction in Error (vedi l’articolo Measures of association for cross classification pubblicato su Journal of the American Statistical Association Vol. 49, pp. 732 – 764). Hanno poi approfondito questi concetti e sviluppato i metodi, presentando con altre misure anche varie forme dell’indice l (lambda) in 3 articoli successivi, dallo stesso titolo e sulla stessa rivista:

-   nel 1959 l’articolo II, su Vol. 54, pp.123-163;

-   nel 1963 l’articolo III, su Vol. 58, pp. 310-364;

-   nel 1972 l’articolo IV, su Vol. 67, pp. 415-421.

 

Nella previsione delle frequenze con cui compare una variabile nominale o categoriale, è possibile utilizzare la sola conoscenza di quella variabile, ma anche quella delle altre: la PRE è data dal rapporto fra le due misure dell’errore.

Si supponga di avere una tavola di contingenza 3 x 3

 

 

 

 

 nella quale è stato riportato quante volte in 144 laghi di una regione, classificati secondo il livello d’inquinamento (alto in 34 laghi, medio in 57 e basso in 53), sono state trovate come prevalenti le tre specie: A (36 volte), B (44) e C (64). Si supponga che la classificazione delle 3 specie, tra loro molto simili, non sia semplice; inoltre che conoscere in quale ambiente vivono, cioè il livello di inquinamento del lago, possa essere una buona indicazione per una classificazione corretta della specie.

(In grassetto è riportato quante volte sono state trovate come prevalenti le 3 specie in laghi a differente livello d’inquinamento; in corsivo, è riportata la proporzione relativa.)

 

La specie che risulta prevalente, cioè quella con la frequenza maggiore o la categoria modale tra le specie, è la C con 64 presenze su 144 casi, pari ad una frequenza relativa di 0,444.

 

La stima della probabilità di una classificazione non corretta P₁ delle specie prevalenti (cioè dell’errore che è possibile commettere), utilizzando solo le informazioni sulla loro morfologia, è 1 meno la probabilità della categoria modale:

P₁  =  1 - 0,444  =  0,556

 

Poiché ognuna delle tre  specie risulta prevalente in un ambiente diverso, per ridurre l’errore e migliorare la classificazione delle specie è possibile utilizzare anche l’informazione sul livello d’inquinamento.

Per ogni gruppo di laghi, classificato sulla base del livello d’inquinamento, dai dati campionari è possibile ricavare quale specie abbia frequenza maggiore:

-   in laghi con inquinamento alto è prevalente la specie A,

-   in laghi con inquinamento medio è prevalente la specie B,

-   in quelli con inquinamento basso è prevalente la specie C.

La probabilità di errore nella classificazione delle specie prevalenti, quando viene usato anche il livello d’inquinamento del lago, è data

-  dalla somma delle probabilità di tutte le celle sulla stessa riga e colonna della cella in questione,

-  esclusa la probabilità relativa alla cella stessa: nella tabella 3 x 3 dell’esempio, è data dalla somma delle 4 frequenze relative

P₂  =  0,056 + 0,069 + 0,118 + 0,042  =  0,285

 ottenendo P₂ = 0,285.

Utilizzando anche l’informazione derivante dalla classificazione del livello d’inquinamento, la probabilità d’errore nella classificazione della specie diminuisce da P₁ = 0,556   a   P₂ = 0,285.

 

Il lambda (l) di Goodman e Kruskal (Goodman-Kruskal lambda) è una misura PRE: valuta la riduzione proporzionale nell’errore, sulla base della relazione

l  = 

Con i dati dell’esempio,

l  =  = 0,487

 si ottiene l = 0,487.

Esso significa che nella classificazione della specie prevalente, quando si utilizza anche l’informazione derivante dal livello d’inquinamento, si ha una riduzione dell’errore pari al 48,7%.

 

Una formula abbreviata, che evita la lunga procedura per ottenere P₁ e P₂, ma che ovviamente mantiene gli stessi concetti, è

l =

 dove

-   f_max   è la frequenza maggiore in ogni RIGA,

-   C_max  è il totale per COLONNA maggiore,

-   N      è il totale generale.

 

Con i dati dell’esempio,

l =  = 0,4875

 

 si ottiene l = 0,4875 (senza gli arrotondamenti prima necessari, con la formula estesa)-

 

Il valore di l varia sempre da 0 a 1.

Il valore 0, che si ottiene quando le frequenze entro ogni casella sono distribuite a caso (calcolabili attraverso il prodotto dei totali di riga e di colonna diviso il totale generale), indica che la variabile indipendente non aggiunge informazioni nella previsione della variabile dipendente e che pertanto non può essere utile nella sua classificazione.

Un valore uguale a 1 indica che esiste corrispondenza perfetta e quindi che la variabile dipendente è classificata correttamente anche dalla variabile indipendente (le specie A, B e C sono rispettivamente presenti sempre e soltanto in laghi con inquinamento alto, basso e medio).

Come già espresso in altre occasioni, non esiste corrispondenza biunivoca tra il valore 0 del lambda e l’associazione tra le due variabili: quando le due variabili sono indipendenti lambda è uguale a 0; ma quando lambda risulta uguale a 0 non sempre si ha indipendenza statistica.

L’indice lambda deve essere usato solo in condizioni particolari di analisi dell’associazione: quando i valori di una variabile qualitativa sono utilizzati per prevedere quelli dell’altra variabile (anche se, come nell’esempio, una variabile è qualitativa e l’altra è di rango).

 

Come è stato proposto il livello d’inquinamento di un lago per predire la presenza della specie prevalente, nello stesso modo è possibile utilizzare la presenza della specie prevalente per indicare il livello d’inquinamento. E’ quindi possibile calcolare un altro valore di lambda, scambiando le righe con le colonne, cioè il previsore con la variabile predetta. Salvo casi fortuiti, di norma i diversi approcci danno risultati differenti. Il lambda presentato è asimmetrico; è quindi importante scegliere la variabile dipendente adatta.

 

In vari casi, come nell’esempio, non è possibile o semplice distinguere tra variabile dipendente ed indipendente. Viene quindi utilizzato un lambda simmetrico, in cui le variabili di riga e di colonna hanno le stesse frequenze.

 

Per spiegare questi concetti con una serie di esempi dettagliati, vengono riportati quelli già utilizzati da Graham J. G. Upton nel suo testo del 1978 The Analysis of Cross-tabuled Data (John Wiley & Sons, Chichester – New York, 1978, reprinted April 1980, da pag. 30 a 32).

 

Data una tabella r x c, con le variabili qualitative A e B, come quella riportata,

 

 

 

 

- l_b stima la diminuzione relativa della probabilità d’errore nell’indovinare la categoria B, utilizzando anche la classificazione di A invece del solo totale marginale di B.

 

I dati che servono (indicati con l’asterisco e in grassetto nella tabella successiva) sono

 

 

-  i valori maggiori in ognuna delle 3 righe A (A₁ = 20;   A₂ = 16;   A₃ = 11),

-  il totale maggiore fra le 4 colonne B (37),

-  il totale generale (120).

 

Da essi si ricava l_b

l_b =

  e si ottiene l_b = 0,120.

 

Invertendo i concetti sulla previsione di A, i dati che servono per stimare l_a (indicati con l’asterisco e in grassetto nella tabella successiva) sono

 

 

 

 

-   i valori maggiori in ognuna delle 4 colonne B (B₁= 11;   B₂ = 16;   B₃ = 18;   B₄ = 20),

-   il totale maggiore fra le 3 righe A (53),

-   il totale generale (120).

 

Da essi si ricava l_a

l_a =

  e si ottiene l_a = 0,179.

Da l_a  e   l_b  mediante

l =

 si ricava l = 0,15 un valore compreso tra l_a  e   l_b.

 

Goodman e Kruskal hanno proposto anche altri metodi, come il t (tau), che per calcolare le probabilità d’errore utilizzano una informazione differente: i totali di riga o di colonna. Questo metodo richiede calcoli più lunghi, nei quali è più facile commettere errori. Di conseguenza, esso non è presentato in modo dettagliato, ma illustrato solamente nei suoi concetti generali.

Quando i dati sono distribuiti in modo indipendente, anche il valore di tau è pari a 0.

Per verificare se il valore ottenuto di l o di t è significativo, si deve ricorrere ad una distribuzione campionaria complessa, che è approssimativamente normale quando N è relativamente grande. Ma, appunto perché asintoticamente normale, la distribuzione campionaria può esser stimata; quindi diventa possibile calcolare il suo errore standard e la sua significatività del valore campionario di l e di t rispetto a quello espresso nell’ipotesi nulla. Data la complessità del calcolo, queste analisi sono possibili solamente attraverso programmi informatici.

Per verificare la significatività di un valore l e un valore t sperimentali con calcoli semplici, manualmente fattibili, è  conveniente utilizzare il valore del c², ottenuto dalla matrice originaria di dimensioni r x c , che ovviamente ha gdl pari a (r-1) x (c-1).

 

Sulla base di concetti analoghi a quelli del l, nel 1972 H. Theil ha proposto un coefficiente di incertezza UC o U (Uncertainty Coefficient, UC or Theil’s U) nel volume Statistical decomposition analysis (Amsterdam, North Holland). E’ chiamato anche coefficiente di entropia (entropy coefficient) e come molti degli indici precedenti ha la proprietà di variare da 0 e 1. La sua originalità consiste nel fatto che  utilizza la teoria dell’informazione per interpretare la PRE, la riduzione proporzionale dell’errore.

L’indice UC di Theil è la percentuale dell’errore nella varianza della variabile dipendente, dove la varianza è definita in termini di entropia. Quando UC = 0, la variabile indipendente o predittiva non fornisce alcun contributo alla stima della variabile dipendente.

E’ una misura asimmetrica.

Per motivi storici, contrariamente alla norma seguita nelle scienze sociali, colloca la variabile dipendente nelle righe. Tuttavia molti programmi informatici, per standardizzare l’input dei dati, seguono la prassi di collocare sulle righe la variabile indipendente e sulle colonne quella dipendente.

E’ simile alla l, come misura di associazione in variabili nominali; ma se ne differenzia, poiché tiene in considerazione tutta la distribuzione, mentre la l utilizza solamente quella modale.

La  UC o U di Theil ha una distribuzione di campionamento nota, per cui è possibile sia calcolare l’errore standard sia effettuare test sulla significatività del valore stimato su dati campionari.