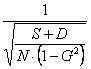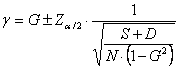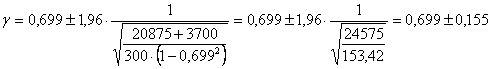COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

20.7.  COGRADUAZIONE PER VARIABILI ORDINALI IN TABELLE r x c:  IL g di GOODMAN E KRUSKALL, IL t_c.DI KENDALL-STUART, IL d_ba E d_ab DI SOMERS.

 

 

In una tabella r x c, in cui le due variabili siano di tipo ordinale, l’associazione viene chiamata con il nome specifico di cograduazione. Pure in questo caso, il punto di riferimento sono le due diagonali; ma in modo più complesso, poiché sono prese in considerazione anche le altre caselle.

Quando la tabella r x c è impostata con le stesse modalità di quella successiva

 

 

 

 

-  la diagonale dai valori bassi verso quelli alti (a – d) è chiamata diagonale della cograduazione,

-  la diagonale opposta (c – d) è chiamata diagonale della contro-graduazione.

 

L’indice di cograduazione più diffuso è il g (presentato anche con il simbolo G) di Goodman e Kruskal presentato nell’articolo del 1954 e  nei 3 successivi, già citati.

Ha una formula analoga al coefficiente bidirezionale Q di Yule

 per tabelle 2 x 2

Q = 

Estesa a una tabella r x c diventa

g  = 

 

In letteratura il g di Goodman e Kruskal è presentato come una misura di correlazione/associazione, in rapporto al fatto che le variabili siano di tipo ordinale (correlazione) oppure nominale (associazione).

Il significato di questo indice, che può essere compreso interpretando la formula per il calcolo, trova la difficoltà maggiore nel capire come sono ottenuti S e D.

 

Più della definizione

-  S = somma delle coppie cograduate, partendo dal valore in alto a sinistra: numero totale di coppie di osservazioni in cui si abbiano sia i>i’ e j>j’ oppure entrambi i<i’ e j<j’

-  D = somma delle coppie cograduate, partendo dal valore in alto a destra: numero totale di coppie di osservazioni in cui si abbiano sia i>i’ e j<j’ oppure entrambi i<i’ e j>j’

 è utile un esempio.

 

A partire dalla tabella

 

 

 

 

 in cui, A e B in questo caso devono essere due variabili ordinali, ranghizzate (ordinate per rango) in modo crescente, il valore di S è determinato dalla somma di più prodotti S_i.

Nel caso specifico della tabella i valori S_i sono sei, ottenuti come indicato di seguito

 

1)  S₁ = 10 (16 + 5 + 13 + 7 + 3 + 4 ) = 10 (48) = 480

 

 

 

2)  S₂ = 5 (5 + 13 + 3 + 4) = 5 (25) = 125

 

 

 

 

3)  S₃ = 18 (13 + 4) = 18 (17) = 306

 

 

 

 

4)  S₄ = 8 (7 + 3 + 4) = 8 (14) = 112

 

 

 

5)  S₅ = 16 (3 + 4) = 16 (7) = 112

 

 

 

 

6)  S₆ = 5 (4) = 20

 

 

 

 

S =  = 480 + 125 + 306 + 112 + 112 + 20 = 1155

 

In modo esattamente simmetrico, il valore di D è ottenuto a partire dal valore in alto a destra

 

1)       D₁ = 20 (8 + 16 +5 + 11 + 7 + 3) = 20 (50) = 1000

2)       D₂ = 18 (8 + 16 + 11 + 7) = 18 (42) = 756

3)       D₃ = 5 (8 + 11) = 5 (19) = 95

4)       D₄ = 13 (11 + 7 + 3) = 13 (21) = 273

5)       D₅ = 5 (11 + 7) = 5 (18) = 90

6)       D₆ = 16 (11) = 176

D = = 1000 + 756 + 95 + 273 + 90 + 176 = 2390

Da S e D si ricava g, indicato spesso con G quando ricavato da dati campionari,

 

Con l’esempio

G  = 

 si ricava G = - 0,348.

Il segno negativo sta ad indicare che a valori bassi di A sono associati valori alti di B, come evidenzia la tabella dei dati.

 

Il valore di G dovrebbe essere calcolato su campioni con un numero totale di conteggi (N) grande. E’ quanto avviene normalmente, poiché G è calcolato in tabelle di grandi dimensioni.

 

Per la significatività di G, appunto perché stimato in grandi campioni, si ricorre alla distribuzione normale Z:

- per verificare l’ipotesi nulla

H₀: g = 0

 contro un’ipotesi alternativa che può essere bilaterale

H₁: g ¹ 0

 quando serve un indice nondirezionale (detto anche bidirezionale),

 

- oppure contro un’ipotesi alternativa unilaterale che può essere

H₁: g > 0     oppure     H₁: g < 0

 quando si è stimato un indice direzionale, il cui segno (positivo oppure negativo) assume un significato preciso nella disciplina analizzata.

 

Il test per la significatività di G è

 dove

- N è il numero totale di osservazioni utilizzate nella tabella

 e SE_G

SE_G =

 è l’errore standard di G.

 

Il valore G calcolato dai dati sperimentali può essere testato non solo rispetto a 0 (H₀: g = 0), ma pure  rispetto a un valore g atteso, specificato nell’ipotesi nulla (ad esempio,  H₀: g = 0,7).

In questa ultima condizione, il test diventa

 

L’intervallo di confidenza di g alla probabilità a prefissata

è

 

Quando il valore G è calcolato per due campioni indipendenti (1 e 2) e in condizioni sperimentali del tutto uguali, cioè se

-  i campioni sono entrambi abbastanza grandi, tanto da poter giustificare per ognuno l’uso della normale,

-  le due tabelle r x c hanno lo stesso numero di righe e di colonne,

-  i livelli di ogni variabile, cioè i gruppi ordinali di ogni variabile, sono identici,

 è possibile confrontare se i due valori G campionari (G₁ e G₂) sono statisticamente uguali,

 cioè  verificare l’ipotesi nulla H₀: g₁ = g₂

con

 in test sia bilaterali che unilaterali.

 

 

ESEMPIO (tratto dal testo di David J. Sheskin del 2000, Parametric and nonparametric statistical procedures, 2^nd ed. Chapman & Hall/CRC, London, 982 p.).

Per valutare se esiste una relazione tra peso alla nascita di un bambino e il suo ordine di nascita, esiste il problema pratico che mentre il primo è misurato su una scala continua, il secondo è una misura di rango con molti valori identici.

A tale scopo, i dati di 300 bambini sono stati aggregati in una tabella r x c, di dimensioni 3 x 4,

 

 

 

 

 in cui il peso è stato aggregato in tre gruppi di dimensioni uguali (100), definiti sotto, uguale e sopra la media.

Calcolare g e verificare la sua significatività.

Inoltre stimare l’intervallo di confidenza di g per a = 0.05

 

Risposta. Scindendo lo sviluppo dell’esempio nei suoi passaggi logici fondamentali,

 

1 - è necessario calcolare S e D

Il valore di S è dato dalla somma dei seguenti 12 prodotti

1)   Cella 11:  70 x (60 + 20 + 10 + 15 + 35 + 40)              = 12600

2)   Cella 12:  15 x (20 + 10 +35+ 40)                                 =   1765

3)   Cella 13:  10 x (10 + 40)                                                =     500

4)   Cella 14:  5 x (0)                                                                             =         0

5)   Cella 21:  10 x (15 + 35 + 40)                                        =     900

6)   Cella 22:  60 x (35 + 40)                                                =   4500

7)   Cella 23:  20 x (40)                                                                         =     800

8)   Cella 24:  10 x (0)                                                                           =         0

9)   Cella 31:  10 x (0)                                                                           =         0

10) Cella 32:  15 x (0)                                                                           =         0

11) Cella 33:  35 x (0)                                                                           =         0

12) Cella 34:  40 x (0)                                                                           =         0

 e risulta S = 20875

 

Il valore di D, iniziando dall’angolo in alto a destra, è dato dalla somma dei seguenti 12 prodotti

1)   Cella 14:  5 x (10 + 60 + 20 + 10 + 15 + 35)                =  750

2)   Cella 13:  10 x (10 + 60 + 10 + 5)                                 =  950

3)   Cella 12:  15 x (10 + 10)                                                =  300

4)   Cella 11:  70 x (0)                                                                           =      0

5)   Cella 24:  10 x (10 + 15 + 35)                                        =  600

6)   Cella 23:  20 x (10 +15)                                                 =  500

7)   Cella 22:  60 x (10)                                                                         =  600

8)   Cella 21:  10 x (0)                                                                           =      0

9)   Cella 34:  40 x (0)                                                                           =      0

10) Cella 33:  35 x (0)                                                                           =      0

11) Cella 32:  15 x (0)                                                                           =      0

12) Cella 31:  10 x (0)                                                                           =      0

 e risulta D = 3700

 

2 – Il valore di G

 risulta G = 0,699.

 

3 - La significatività del valore sperimentale ottenuto  G = 0,699, cioè la verifica dell’ipotesi nulla

H₀: g = 0

 contro l’ipotesi alternativa bilaterale oppure unilaterale è

 

 data da Z = 8,847.

In una distribuzione normale, Z è altamente significativo sia considerando un test bilaterale che unilaterale.

 

4 - L’intervallo di confidenza (con Z = 1,96 in quanto richiesto per a = 0.05 in una distribuzione bilaterale)

 

 è uguale a 0,699 ± 0,155

 e quindi come

- limite inferiore ha l₁ =  0,699 – 0,155 = 0,544

- limite superiore ha l₂ = 0,699 + 0,155 = 0,854

 

 

Il coefficiente t_c di Kendall (Kendall’s tau-c), chiamato anche t_c di Stuart (Stuart’s tau-c) o  t_c di Kendall-Stuart (Kendall-Stuart tau-c) è una estensione del t_b (specifico per tabelle 2 x 2 e già presentato) a tabelle di dimensioni maggiori, cioè r x c.

Il t_c di Kendall-Stuart è un coefficiente di cograduazione; è uguale all’eccesso di coppie concordanti su quelle discordanti, con aggiustamento per le dimensioni del campione.

Con i simboli usati in precedenza per il g

 il t_c è dato da

 in cui

-   S e D sono uguali alla formula precedente ed ovviamente calcolati nello stesso modo,

-   T_a = numero totale di coppie di osservazioni in cui i = i’: è la somma dei prodotti di ogni valore per la somma di quelli che sulla stessa riga stanno alla sua destra, a partire dalla prima colonna;

-   T_b = numero totale di coppie di osservazioni in cui j = j’: è la somma dei prodotti di ogni valore per la somma di quelli che stanno sotto di lui, nella stessa colonna, a partire dalla prima riga.

 

Dalla stessa tabella utilizzata in precedenza

 

 

 si ricava che  T_a è la somma di 9 valori, dei quali vengono riportati dettagliatamente tutti i calcoli, come spiegazione del metodo:

1)  T_a1  =  10 (5 + 18 + 20) = 10 (43)   = 430

2)  T_a2  =  5 (18 + 20) = 5 (38)                             = 190

3)  T_a3  =  18 (20)                                  = 360

4)  T_a4  =  8 (16 + 5 + 13) = 8 (34)       = 272

5)  T_a5  =  16 (5 + 13) = 16 (18)           = 288

6)  T_a6  =  5 (13)                                    =   65

7)  T_a7  =  11 (7 + 3 + 4) = 11 (14)       = 154

8)  T_a8  =  7 (3+4) = 7 (7)                     =   49

9)  T_a9  = 3 (4)                                                       =   12

  T_a =  = 430 + 190 + 360 + 272 + 288 + 65 + 154 + 49 + 12 = 1820

 

 T_b ( sempre in questa tabella specifica) è la somma di 8 valori:

1)  T_b1  =  10 (8 + 11) = 10 (19)           = 190

2)  T_b2  =  8 (11)                                    =   88

3)  T_b3  =  5 (16 + 7) = 5 (23)                               = 115

4)  T_b4  =  16 (7)                                    = 112

5)  T_b5  =  18 (5+3) = 18 (8)                 = 144

6)  T_b6  =  5 (3)                                                      =   15

7)  T_b7  =  20 (13 + 4) = 20 (17)           = 340

8)  T_b8  =  13 (4)                                    =   52

  T_b =  = 190 + 88 + 115 + 112 + 144 + 15 + 340 + 52 = 1056

 

Applicando la formula di Kendall, si ottiene

 

 

 un valore di t_C = –0,497.

 

L'elevato numero di calcoli richiesti, anche se semplici, possono determinare errori.

E’ quindi utile avvalersi della proposta per la verifica della correttezza di tutti i parametri considerati,

 attraverso la relazione

N² = 2×(S + D + T_a + T_b) +

 dove

-   N²  è il quadrato della somma di tutti i dati della tabella,

-   S, D, T_a e T_b sono i 4 valori utilizzati per la stima dell’indice,

-    è la somma dei quadrati di tutti i singoli valori della tabella.

 

Con i dati della tabella utilizzata,   è

 

 

 

 uguale a 1558; di conseguenza, con

N = 120;   S = 1155;   D = 2390;   T_a = 1820;   T_b = 1056

 si dimostra

120² = 2 (1155 + 2390 + 1820 + 1056) + 1558 = 14400

 

 l’uguaglianza delle due quantità (entrambe danno lo stesso risultato di 14400): è testimoniata la correttezza di tutti i parametri calcolati in precedenza.

 

Nel 1962 R. H. Somers (con lo stesso articolo citato per il D asimmetrico, A new asymmetric measure of association for ordinal variables, pubblicato su American Sociological Review Vol. 27, n. 6, pp. 700-811) ha proposto anche indici (d_ba e d_ab) di cograduazione asimmetrici o unidirezionali per tabelle r x c, da applicare nel caso di variabili ordinali.

Come nel titolo dell’articolo, questo indice e i precedenti (gamma, tau-b e tau-c) sono chiamate anche misure di associazione ordinale (ordinal association).

 

Quando B è la variabile dipendente (e ovviamente A la variabile indipendente), si può stimare d_ba con

 

Questa statistica è distribuita in modo approssimativamente normale. La sua varianza è stata stimata da L. A. Goodman e E. H. Kruskal nel 1972 (con l’articolo Measures of association for cross-classification, pubblicata dalla rivista Journal of the American Statistical Association, Vol. 67, pp. 415-421).

 

Quando A è la variabile dipendente, si stima d_ab con

con formula simmetrica.

 

Utilizzando sempre la stessa tabella, con S = 1155;   D = 2390;   T_a = 1820;   T_b = 1056

-  d_ba

 risulta uguale a –0,268 e

 

- d_ab

 risulta uguale a –0,230.

 

In un confronto tra questi diversi indici, Graham J. G. Upton nel suo volume del 1978 (The analysis of cross-tabuled data, pubblicato da John Wiley & Sons, Chichester, a pag. 38) consiglia, giustificandola come pura scelta personale, di preferire:

-  per dati nominali, il l di Goodman e Kruskal,

-  per dati ordinali, il g se le due variabili sono di importanza uguale,

-  rispettivamente il l_b di Goodman e Kruskal  o il d_ba di Somers, se la variabile B dipende dalla variabile A.