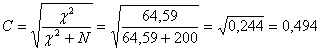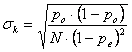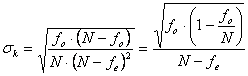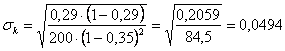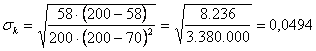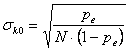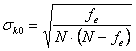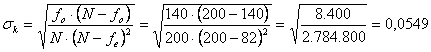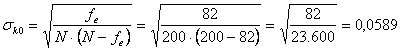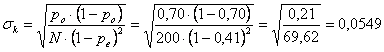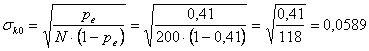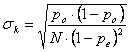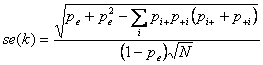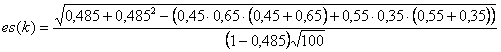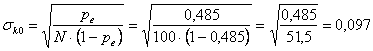COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

20.8.  IL KAPPA DI COHEN: STIMA DELL’ACCORDO (AGREEMENT) TRA DUE VALUTAZIONI CON SCALA NOMINALE.

 

 

Le misure del grado di associazione, la cui significatività è ottenuta con il test c² e/o il test G, fanno riferimento a due variabili. Ad esempio, nelle tabelle 2 x 2 del c² si è valutato il grado di associazione tra livello di inquinamento (alto o basso) di un’area e la presenza di persone residenti con malattie polmonari (si o no); in termini diversi ma con lo stesso concetto, nelle tabelle M x N si è verificata l’indipendenza tra presenza di specie e tipologia del lago.

In altre situazioni, che sono illustrate in questo paragrafo, si utilizza una sola variabile per valutare il grado di accordo tra due valutatori. Ad esempio, in medicina può essere interessante verificare se due chirurghi che decidono sulla necessità di operare forniscono risposte concordanti; nella ricerca ambientale, se due commissioni che agiscono in modo indipendente approvano o respingono gli stessi progetti; in psicologia e nelle scienze forensi, se due giurie assolvono o condannano gli stessi imputati, ovviamente sempre trovandosi nelle stesse condizioni di valutazione.

Un problema identico si pone anche per lo stesso valutatore, quando opera in due momenti differenti. Ad esempio, se lo stesso chirurgo fornisce o meno la medesima risposta sulla necessità di un intervento chirurgico prima e dopo aver preso visione di una nuova analisi clinica; se un ricercatore, di fronte agli stessi soggetti in due momenti differenti, fornisce la stessa classificazione.

In casi più complessi, nella ricerca applicata sovente a due o più esperti è chiesto di catalogare una serie di oggetti, piante, animali o persone in gruppi qualitativi o nominali. In biologia e agraria può essere la classificazione di specie animali o vegetali; in medicina l’individuazione della malattia o la sua causa in un gruppo di pazienti.

 

In una visione più generale, il problema è importante tutte le volte in cui si confrontano due o più distribuzioni di frequenza, tratte da ricerche o da pubblicazioni differenti. L’appartenenza dell’esperto a scuole con impostazioni culturali differenti e la diversa esperienza dei ricercatori possono determinare classificazioni troppo discordanti, per effettuare correttamente test sulla similarità della distribuzione. Ad esempio, con una tabella 2 x 2 oppure a più dimensioni (M x N) spesso si vuole valutare se M specie hanno la stessa distribuzione nelle N aree campionate. Ma tale analisi come condizione di validità richiede necessariamente che la classificazione delle specie abbia seguito gli stessi criteri. In altri termini, che la classificazione sia riproducibile, che i criteri utilizzati siano affidabili (reliability studies, where on wants to quantify the reproducibility of the same variable measured more than once).

Il problema non è valutare quale delle due classificazioni sia quella corretta o la migliore; è una domanda alla quale è possibile rispondere con una impostazione logica e con  metodi differenti.

 

Il kappa di Cohen è una misura dell’accordo (coefficient of agreement) tra le risposte qualitative o categoriali di due persone (inter-observer variation) oppure della medesima persona in momenti differenti (intra-observer variation), valutando gli stessi oggetti. Tra i testi internazionali di statistica non parametrica, il k di Cohen è riportato in P. Sprent e N. C. Smeeton del 2001 (Applied nonparametric statistical methods, 3^rd ed. Chapman & Hall/CRC, London, XII + 461 p.).

 

La metodologia è stata presentata da Jacob Cohen della New York University nel 1960 (con l’articolo A coefficient of agreement for nominal scales, pubblicato su Educational and Psychological Measurement, Vol. XX, No. 1, pp. 37-46) per il caso più semplice. Secondo l’autore, il test trova i presupposti nell’articolo di W. A. Scott del 1955 (Reliability of content analysis: the case of nominal scale coding, pubblicato da Public Opinion Quarterly, Vol. XIX, pp.321-325).

Cohen sviluppa un esempio con un linguaggio estremamente semplice, caratteristico di quasi tutte le riviste di psicologia sulle quali questo test è stato in prevalenza proposto e discusso. Pertanto questa presentazione riporta il suo testo in modo quasi integrale.

Riprendendo una situazione caratteristica della ricerca psicologica, si supponga che due medici abbiano analizzato separatamente e in modo indipendente il comportamento delle stesse 200 persone, classificandole in tre differenti tipologie nominali (A = disordini della personalità, B = neurosi, C = psicosi), con i seguenti risultati:

 

 

 

 

Si tratta di valutare se i giudizi forniti dai due esperti sono riproducibili, affidabili (reproducible, reliable); in altri termini, si chiede di determinare il grado, la significavità e la stabilità campionaria del loro accordo (the degree, significance, and sampling stability of their agreement).

 

Per il coefficiente di concordanza, devono essere realizzate le seguenti condizioni di validità:

1 -   le unità (in questo caso i 200 soggetti analizzati) sono indipendenti;

2 -   le categorie della scala nominale sono indipendenti, mutuamente esclusive e esaustive;

3 -   i giudici operano in modo indipendente.

Queste assunzioni ne implicano altre due:

4 -   i due giudici hanno lo stesso livello di competenza;

5 -   non esistono restrizioni nell’attribuzione alle categorie.

 

Per entrare nella logica del test, è importante comprendere che se la classificazione dei pazienti fosse effettuata su criteri indipendenti, cioè se le due serie di attribuzioni fossero realizzate in modo puramente casuale, si avrebbe ugualmente un certo numero di giudizi coincidenti: un paziente potrebbe essere attribuito alla stessa categoria, per solo effetto del caso. Per meglio illustrare il concetto di concordanza e evidenziare la logica che porta a ricavare l’indice k proposto da Cohen, è vantaggioso utilizzare le proporzioni riportate nella tabella successiva. Esse sono semplicemente la trasformazione in frequenze relative (con totale uguale a 1,0) delle frequenze assolute precedenti (con totale uguale a 200)

 

 

 

 

Entro ogni casella,

-   in grassetto sono riportate le proporzioni osservate (p_o da observed); ad esempio, nella casella 1,1 si ha 0,25 = 50/200 (presi dalla tabella precedente con le frequenze assolute),

-  in corsivo quelle attese (p_e da expected), nella condizione che l’ipotesi nulla sia vera, cioè che l’attribuzione dell’individuo alla categoria sia stata casuale; ad esempio sempre nella 1,1 si ha 0,20 = 0,4 x 0,5 (totali marginali presi da questa ultima tabella di frequenze relative).

Come nelle tabelle del chi quadrato, le proporzioni attese entro ogni casella sono date dai prodotti delle proporzioni marginali.

 

Si tratta di valutare quanto differiscono le classificazioni effettuate dai due medici.

 

Prima di Jacob Cohen, era seguita la procedura proposta nel 1950 da J. P. Guilford nel testo Fundamental Statistics in Psychology and Education (2^nd ed., New York, McGraw-Hill). In esso si ricorre al c², per stimare la significatività, e al coefficiente di contingenza C di Pearson, per ricavare una misura dell’accordo che sia più facilmente valutabile, cioè indipendente dalle dimensioni del campione. Con i dati dell’esempio,

-   per ottenere  il c² mediante la formula applicata alle proporzioni

 si stimava

 con 4 gdl

 

-  per il C di Pearson si stimava

 

Jacob Cohen contesta questo metodo.

Poiché il risultato del c² è altamente significativo (infatti il valore critico del c² con 4 gdl e a = 0.001 è 18,467), quindi si allontana dall’ipotesi di distribuzione casuale, alcuni ricercatori potevano dichiararsi soddisfatti e ritenere di avere provato l’esistenza di un accordo adeguato tra i due valutatori (at this point some investigators would rest content that agreement is adeguate). In realtà, egli scrive, è semplice dimostrare che l’uso del c² e quindi del C fondato su di esso sono logicamente indifendibili, come misura dell’accordo.

Quando è applicato a una tabella di contingenza, il test c² serve per

-  verificare l’ipotesi nulla rispetto all’associazione, non alla concordanza

(anche se la distribuzione dell’ipotesi nulla è calcolata nello stesso modo). Infatti, come nel caso dell’esempio, sul valore totale = 64,59 il contributo maggiore è dato dalla casella 3,2

con

 un c² parziale uguale a 27,00.

 

Questo valore così alto non dipende dall’accordo tra i due medici, ma dal fatto opposto: essi hanno fornito una classificazione differente degli stessi pazienti (cioè la malattia B per il medico 1 e la malattia C per il medico 2) e in misura maggiore dell’atteso, cioè delle frequenze fondate sull’ipotesi nulla di casualità. Quindi il valore ottenuto risulta elevato, non perché i due medici concordano, ma perché essi non concordano. Più in generale, il valore del c² misura se due distribuzioni qualitative sono associate (non importa se in modo positivo o negativo, trattandosi di valori elevati al quadrato), ma senza fornire la direzione dell’accordo, che è l’aspetto fondamentale e specifico di questa valutazione della concordanza.

 

Come conclusione dei concetti precedenti, si deduce che una misura dell’accordo tra le due distribuzioni può essere ricavata

-   dalla differenza tra la proporzione osservata dei giudizi che sono effettivamente coincidenti e la proporzione di quelli attesi nell’ipotesi di totale casualità dei giudizi (H₀ vera),

-  rapportata a quella della non associazione attesa.

 

In altri termini, la formula proposta da Cohen standardizza la differenza tra proporzione totale osservata e proporzione totale attesa, dividendola per la massima differenza possibile non casuale.

Nelle ultime due tabelle dei dati, l’informazione utile è fornita dalle frequenze collocate lungo la diagonale principale (nella tabella 3 x 3, le caselle 1,1; 2,2; 3,3).

Nel caso dell’esempio, con le proporzioni la somma della diagonale principale

-  0,25 + 0,02 + 0,02 = 0,29 è la proporzione totale osservata p_o = 0,29

-  0,20 + 0,09 + 0,06 = 0,35 è la proporzione totale attesa p_e = 0,35.

 

L’indice k proposto da Cohen

 è

 

Con le frequenze assolute, sovente è possibile una stima più semplice e rapida.

Dopo aver calcolato

-  le frequenze osservate f_o = 50 + 4 + 4 = 58  (nella prima tabella)

-  e quelle attese f_e = 40 + 18 + 12 = 70  (nella tabella sottostante)

 

 

 

 utilizzando appunto solo i valori collocati sulla diagonale principale,

 il calcolo dell’indice k diventa

 

Con entrambe le formule, il valore dell’accordo risulta k = -0,09. In questo caso, è un valore negativo.

Esso indica che i due medici si trovano d’accordo su una proporzione di casi che è minore di quella che si sarebbe ottenuta con una attribuzione casuale dei pazienti alle varie categorie. In conclusione, i due medici forniscono valutazioni tendenzialmente contrapposte( anche se per una quantità minima).

 

Il valore di k teoricamente può variare tra – 1 e + 1. In realtà l’indice k ha significato solo quando è positivo.

Da questa osservazione derivano due conseguenze:

1 - la sua significatività deve essere verificata mediante il test unilaterale:

H₀: k £ 0      contro      H₁: k > 0

2 - il valore massimo teorico è k = +1,0.

 

Questa ultima affermazione è vera, cioè si può ottenere k = +1, solamente quando sono realizzate contemporaneamente le seguenti due condizioni:

1 -  tutte le celle non collocate sulla diagonale, cioè quelle che indicano il disaccordo (disagreement) sono 0.

2 - i totali marginali dei due valutatori (cioè i totali delle righe e quelli delle colonne) sono identici.

 

Infatti essi indicano che i due valutatori hanno trovato le stesse proporzioni delle categorie utilizzate. Nella tabella con le proporzioni fino ad ora utilizzata, le frequenze marginali dei due medici sono differenti, esattamente quelle riportate nella tabella sottostante (per il medico 1 esse sono 0,40,  0,30,  0,30; per il medico 2 sono 0,50,  0,30,  0,20)

 

 

 

 

A causa di questa differenza nei totali marginali, il k massimo (k_M) ottenibile con la formula precedente non potrà mai essere k = +1,00 ma un valore inferiore. Tale valore massimo possibile può essere ricavato con alcuni passaggi:

1) confrontare i singoli totali marginali (prime due righe della tabella) e per ogni categoria scegliere il valore minore (terza riga in grassetto e corsivo),

2) calcolare p_oM, la proporzione osservata massima, utilizzando la somma di queste proporzioni minime:

p_oM =  0,40 + 0,30 + 0,20 = 0,90

3) stimare il k massimo (k_M) con

Con i dati dell’esempio, dove

-  p_oM = 0,90

-  p_e = 0,35

 mediante

 

 si ricava che il valore massimo possibile di k, é k_M = 0,846.

E’ una conseguenza del fatto che i due valutatori forniscono una classificazione differente degli stessi soggetti, poiché per le categorie in oggetto essi “vedono” frequenze differenti nella stessa popolazione.

 

Da questa prima analisi sul k_M può derivare un primo effetto.

Per ottenere ricerche più attendibili, dove k_M sia 1,  sarebbe vantaggioso fornire indicazioni più vincolanti ai due valutatori, con una preparazione preliminare. Dopo il corso, valutare nello stesso modo se il k_M è migliorato.

Una seconda conseguenza potrebbe essere quella di stimare un valore di k corretto (k_C),

 attraverso la relazione

 

 in modo che il valore massimo raggiungibile sia sempre 1 e quindi sia la scala di valutazione sia i confronti siano omogenei.

Ma Cohen sconsiglia tale trasformazione, che nel ragionamento precedente appariva logica e razionale, con la motivazione che se i totali marginali sono differenti è perché i due valutatori hanno fornito effettivamente risposte differenti. Quindi esiste un reale non-accordo nella valutazione, che giustamente è compreso nell’indice k calcolato senza la correzione.

 

Nella presentazione di questo metodo, dopo la illustrazione

a)  del significato di k,

b)  del calcolo del valore k

c)  e di quello massimo possibile (k_M),

 si pongono altri tre problemi:

d)  stimare l’intervallo di confidenza di k,

e)  valutare la significatività statistica e il significato disciplinare del risultato, cioè del valore di k ottenuto,

f)  testare la significatività della differenza tra due valori di k.

 

Nel caso di grandi campioni (N ³100), per calcolare l’intervallo di confidenza di k secondo Cohen  è possibile il ricorso alla distribuzione normale standardizzata,

 dove  è un errore standard (pure essendo indicato come una deviazione standard) in quanto k è una media.

Il valore di  può esser calcolato utilizzando

-  sia le frequenze relative o proporzioni

-  sia le frequenze assolute

 

I limiti di confidenza di kappa sono compresi

-  con probabilità del 95% tra

-  con probabilità del 99% tra

 

Utilizzando i dati dell’esempio,

- sia mediante la tabella delle frequenze relative o proporzioni, dove p_o = 0,29  e  p_e = 0,35  e  N = 200,

 

 

- sia mediante la tabella delle frequenze assolute, dove f_o = 58  e  f_e = 70  e  N = 200,

 

 si ottiene  = 0,0494.

Poiché  il valore sperimentale ricavato è k = - 0,09, alla probabilità del 95% il valore reale di k è compreso

-0,09 ± 1,96 ×0,0494

 tra il valore minimo  = - 0,138  (–0,09 – 0,048)

 e il valore massimo = - 0,042 (–0,09 + 0,0489).

 

Per la significatività statistica di k, teoricamente per valutare l’ipotesi nulla H₀: k = 0 che è ottenibile quando p_o = p_e, la formula dell’errore standard :

- con le frequenze relative diventa

 

- con le frequenze assolute diventa

 

Con i dati dell’esempio,

- sia mediante la tabella delle frequenze relative o proporzioni, dove   p_e = 0,35  e  N = 200,

 

 

- sia mediante la tabella delle frequenze assolute, dove   f_e = 70  e  N = 200,

 

 si ottiene = 0,0519.

 

Nella significatività di un k sperimentale, per la sua rilevanza pratica ai fini della potenza del test e un approccio teoricamente più corretto, è importante ricordare un concetto già evidenziato. Benché, in un esperimento reale, il valore di k possa variare tra –1 e +1, quasi sempre nella ricerca si vuole valutare se esiste un accordo significativo.

Pertanto in realtà il test è unilaterale con ipotesi

H₀: k £ 0      contro      H₁: k > 0

 

Sempre Cohen, per il test di significatività con grandi campioni (N ³100) e come quasi sempre avviene quando si utilizzano tabelle di dimensioni superiori a 2 x 2, propone il ricorso alla distribuzione normale standardizzata

Nel caso dell’esempio, il valore di k è risultato negativo (k = -0,09).

Di conseguenza, non ha senso verificare se è maggiore di zero (cioè H₁: k > 0), cioè se esiste un accordo che sia contemporaneamente positivo e significativo, tra i due medici nella classificazione da essi effettuata per gli stessi pazienti.

 

Nelle due formule dell’errore standard (  e  ), utili

- il primo () per l’intervallo di confidenza

- il secondo  () per la significatività di k,

si evidenzia che il numero totale di osservazioni (N), ha un ruolo importante. Ne deriva che, come in quasi tutti i test, con grandi campioni anche un valore di k piccolo può risultare significativo, mentre con un campione piccolo anche un valore grande di k può non essere statisticamente significativo.

 

Per sfuggire a questi limiti e per ottenere una interpretazione univoca e adimensionale di k come stima di Agreeement o Reproducibility, sono state proposte griglie (benchmarks) di valutazione. Nella tabella successiva, sono riportate le due più frequentemente utilizzate.

 

 

 

 

La prima, a sinistra e più dettagliata, è stata proposta da J. Richard Landis e Gary G. Koch del 1977 (The measurement of observer agreement for categorial data pubblicato da Biometrics, Vol. 33, pp. 159-174).

La seconda, riportata a destra, è stata proposta da Joseph L. Fleiss nel suo testo del 1981 Statistical Methods for Rates and Proportions (John Wiley & Sons). Più semplice, è ripresa da alcuni testi a carattere divulgativo, tra cui il volume di Bernard Rosner del 2000 Fundamentals of Biostatistics (5^th ed. Duxbury, Australia, XVII + 792 p.).

 

 

ESEMPIO 1 (tratto dall’articolo di Cohen del 1960). Valutare il grado di accordo tra due giudici nella seguente tabella 3 x 3  (tra parentesi e in grassetto sono evidenziate le frequenze attese e quelle osservate limitatamente alla diagonale, in quanto sono le uniche informazioni utili).

 

 

 

 

Risposta.   Dopo aver ricavato

- le frequenze osservate  f_o = 88 + 40 + 12 = 140

- le frequenze attese   f_e = 60 + 18 + 4 = 82

 è semplice osservare che in questo caso esiste un accordo maggiore di quello possibile per solo effetto del caso.

 

Dalle frequenze si ricava il valore di k

 che risulta k = 0,492.

Per il calcolo dell’intervallo di confidenza si stima

 

 

 l’errore standard  = 0,0549.

 

Per il test che verifica la significatività dell’accordo si stima

 

 l’errore standard  = 0,0589.

 

Questi stessi risultati possono essere ottenuti con la tabella delle frequenze relative o proporzioni

 

 

 

 

 sempre ricordando che N = 200.

Dopo aver ricavato

- le frequenze relative osservate  p_o = 0,44 + 0,20 + 0,06 = 0,70

- le frequenze relative attese   p_e = 0,30 + 0,09 + 0,02 = 0,41

 si stima il valore di k

 che risulta k = 0,492.

 

Con le frequenze relative, può essere utile calcolare il valore k_M

 

 

Per il calcolo dell’intervallo di confidenza si stima

 

 l’errore standard  = 0,0549.

Per il test che verifica la significatività dell’accordo si stima

 

 l’errore standard  = 0,0589.

 

Con k = 0,492 e   = 0,0549 si ottiene l’intervallo di confidenza.

Alla probabilità del 95% esso è compreso

 =

- tra il valore minimo = 0,384 (0,492 - 0,108)

-  e il valore massimo = 0,600 (0,492 + 0,108).

 

La significatività statistica del valore k = 0,492 cioè la verifica dell’ipotesi

H₀: k £ 0      contro      H₁: k > 0

 con

  determina Z = 8,35

Nella distribuzione normale unilaterale, a Z = 8,35 corrisponde una probabilità P < 0.0001.

L’interpretazione conclusiva è che esiste un accordo statisticamente significativo, ma oggettivamente non alto. Infatti ha un livello o una intensità

-  moderate secondo una classificazione,

-  good secondo l’altra.

In queste condizioni, ai fini dell’interpretazione appare più utile l’intervallo di confidenza: il valore reale di kappa è compreso in una scala molto ampia, essendo incluso con probabilità del 95% tra

-  un livello fair,  nel limite inferiore (k = 0,384) e

-  un livello moderate, nel limite superiore (k = 0,600).

Anche utilizzando l’altra scala, con probabilità alta il valore reale di k potrebbe essere giudicato sia marginal sia good.

 

Per la significatività della differenza tra due k indipendenti (k₁ – k₂), dove l’ipotesi alternativa ovviamente può essere sia unilaterale sia bilaterale, Cohen propone

 

 dove

 

 per ognuno dei due campioni in modo indipendente

 

Per il calcolo dell’errore standard di k, necessario alla verifica dell’ipotesi nulla H₀: k = 0, è stata proposta una nuova formula asintotica, quindi per grandi campioni e con l’uso della distribuzione Z, da J. L. Fleiss, J. C. M. Lee e J. R. Landis nel 1979 (con l’articolo The large sample variance of kappa in the case of different sets of raters, pubblicato su Psychological Bulletin Vol. 86, pp. 974-977). Come riportata nel testo di Sprent e Smeeton citato, indicata con se(k)

 essa è

 

Può essere utile il confronto con quella originaria di Cohen, dalla quale differisce per il numeratore, come svolto nell’esempio successivo.

 

 

ESEMPIO 2 (tabella 2 x 2 tratta dal testo di Sprent e Smeeton, modificata a scopi didattici per maggiore chiarezza).

Un dentista ha registrato sulle cartelle dei pazienti la sua opinione circa la necessità di estrarre il dente cariato, prima e dopo la radiografia. 

Il conteggio delle valutazioni ha dato i seguenti risultati

 

 

 

Fornire una misura quantitativa della variazione di giudizio o inversamente della riproducibilità del giudizio nei due diversi esami (a quantitative measure of reproducibility between the responses at the two surveys).

 

Risposta.   Benché i calcoli possano essere effettuati indifferentemente con le frequenze assolute e con quelle relative, per una visione più chiara dei risultati è vantaggioso utilizzare quelle relative.

Dopo trasformazione, i dati diventano

 

 

 

 

 ricordando che

-  in grassetto sono riportate le proporzioni osservate,

-  in corsivo e tra parentesi quelle attese e che

-  il numero totale di osservazioni è N = 100.

(Per i calcoli successivi, è sempre bene avere almeno 3-4 cifre decimali).

 

Dopo aver ottenuto p_o = 0,40 + 0,30 = 0,70    e    p_e = 0,2925 + 0,1925 = 0,485

 si ricavano

 

- il valore di k

- il suo errore standard es(k)

 

 

 

La significatività di k per la verifica di

H₀: k £ 0      contro      H₁: k > 0

 fornisce un valore

 

Il risultato (Z = 4,53) è così grande che, nella tabella della distribuzione normale standardizzata unilaterale, corrisponde a un probabilità P < 0,0001.

Se ne deve dedurre che il valore di k è altamente significativo, quindi statisticamente maggiore di zero. Tuttavia, poiché k = 0,417 non è molto alto, il grado di accordo tra le due distribuzioni è

-  moderate secondo la scala di Landis e Koch

-  good secondo quella di Fleiss.

 

Con la formula di Cohen

 

 

 l’errore standard sarebbe risultato  = 0,097.

E’ un valore più grande e quindi fornisce una stima di Z più prudenziale (più bassa) ai fini del rifiuto dell’ipotesi nulla k = 0; ma la differenza con il risultato precedente è ridotta.

Con questo valore dell’errore standard,

 il risultato del test per la significatività

 sarebbe stato Z = 4,30.

Non avrebbe modificato sostanzialmente l’interpretazione del risultato ottenuto con l’errore standard precedente.

Benché alcuni testi di statistica applicata propongano solo la nuova formula, altri testi evidenziano che per essa la condizione di normalità è più vincolante e che pertanto in esperimenti standard, con campioni inferiori alle 100 unità, sia preferibile utilizzare sempre quella proposta da Cohen.

 

Anche per l’intervallo di confidenza più recentemente è stata proposta una formula asintotica dell’errore standard di k, che con grandi campioni appare più precisa. E’ stata presentata da J. L. Fleiss nel 1981, nel volume Statistical Methods for Rates and Proportions (2^nd ed. New York, John Wilwy & Sons). Secondo altri autori di testi divulgativi, fondamentalmente non è migliore e ha gli stessi limiti dell’altra già proposta per il test di significatività: fornisce risultati non molto dissimili da quella di Cohen, è più vantaggiosa per la significatività, ma è meno valida per i campioni effettivamente raccolti in molte ricerche, che sono inferiori a 100 unità.

 

SVILUPPI SUCCESSIVI

Una breve presentazione degli sviluppi del k di Cohen è rintracciabile nell’articolo del 1990 di Posner e alii (Karen L. Posner, Paul D. Sampson, Robert A. Caplan, Richard J. Ward and Frederick W. Cheney)  intitolato Measuring interrater reliability among multiple raters: an example of methods for nominal data, (pubblicato su Statistics in Medicine, Vol. 9, pp. 1103-1115). Tali sviluppi hanno riguardato fondamentalmente tre aspetti:

-   il tipo di scala (con il Weighted kappa), che da nominale è diventata prima ordinale e poi di rapporti; in queste, l’errore di classificazione può avere gravità differenti e può essere valutato; l’argomento era già stato discusso dallo stesso Cohen nel 1968 (con l’articolo Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit, pubblicato su Psychological Bulletin, Vol. 70, No. 4, pp. 213-220);

-  il numero di valutatori (Multiple kappa), esteso da due a più già da J. L. Fleiss nel 1971 (nell’articolo Measuring nominal scale agreement among many raters, su Psycological Bulletin, vol. 76, pp. 378-382) e da J. Richard Landis e Gary G. Koch nel 1977 (The measurement of observer agreement for categorial data pubblicato da Biometrics, Vol. 33, pp. 159-174);

-  il numero di sottopolazioni, eventualmente giudicate da più valutatori (Generalized kappa), con la stima del peso di ogni categoria.

 

Alcuni di questi sviluppi e una ampia discussione sul k di Cohen sono illustrati nel paragrafo successivo.