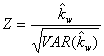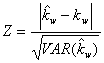COEFFICIENTI DI ASSOCIAZIONE, DI COGRADUAZIONE E DELL’ACCORDO

RISCHIO RELATIVO E ODDS RATIO

 

 

20. 9.  ALCUNI SVILUPPI DELLA STATISTICA KAPPA: LA K PESATA E I PARADOSSI

(di Sonia Cipriani dell’Istituto di Ricerche Farmacologiche “Mario Negri” di Milano. Mail: cipriani@marionegri.it).

 

 

L’idea della statistica kappa pesata nasce, con l’estensione dell’applicazione di tale statistica a variabili di tipo ordinale, allo scopo di discriminare tra gradi diversi di disaccordo. Secondo questa logica, il disaccordo nell’attribuzione di un’unità a due categorie differenti è da ritenere, infatti, meno grave se le due categorie di attribuzione sono confinanti; è invece via via più grave, quanto più le categorie di attribuzione sono distanti nella scala ordinale.

Sulla base di questa considerazione, Cohen (1968) propone di introdurre nel computo della statistica kappa dei pesi   da assegnare alle celle in modo da esprimere la gravità o intensità del disaccordo.

Tali pesi possono assumere valori nell’intervallo [0-1] e devono essere tali che:

-  alle celle di perfetto accordo, cioè quelle sulla diagonale principale, venga attribuito il massimo peso:

  

-  a tutte le celle di disaccordo venga assegnato un peso minore di quello massimo:

    

-  i pesi devono essere attribuiti in modo simmetrico rispetto ai due osservatori:

La proporzione di accordo osservato pesato

 diventa quindi:

 

 e la proporzione di accordo ponderato,

 atteso per il solo effetto del caso, diventa:

 

Date queste premesse,

 la statistica kappa pesata (K_w) è:

 

Notiamo che quando i pesi sono tutti uguali a 0 fuori dalla diagonale ( per ogni ), cioè quando tutti i livelli di disaccordo sono considerati ugualmente gravi, la statistica kappa pesata diviene identica alla kappa non pesata.

Un punto fondamentale di questa metodologia è: il valore della statistica kappa pesata ottenuto dipende

-  sia dall’accordo osservato,

-  sia dalla scelta dei pesi.

 

A parità di accordo osservato, infatti, si otterranno valori differenti della statistica kappa a seconda delle ponderazioni scelte. Al fine di uniformare la scelta dei pesi e di rendere, quindi, confrontabili tra loro i valori della kappa pesata ottenuti da differenti studi, sono state proposte in letteratura le seguenti formule di ponderazione:

-  Pesi quadratici, Fleiss e Cohen (1968):

 

-  Pesi assoluti, Cohen (1968), Cicchetti e Allison (1971):

 

Nel caso di una variabile a quattro categorie, i pesi calcolati sarebbero

 

 

La distribuzione di campionamento della statistica kappa pesata è stata

-  derivata da Fleiss, Cohen e Everitt (1969) e

-  confermata da Cicchetti e Fleiss (1977), Landis e Koch (1977a), Fleiss e Cicchetti (1978), e Hubert (1978).

 

La varianza della statistica kappa pesata (VAR(K_w)), sotto l’ipotesi nulla ,

  è :

dove:

          e         

 

L’ipotesi nulla  può essere, quindi, saggiata mediante

 la statistica test:

 

 rifiutando l’ipotesi nulla per valori di  maggiori rispetto ai valori critici riportati nelle tabelle della distribuzione normale standardizzata.

 

Un altro test proposto per saggiare l’ipotesi che il vero valore della kappa pesata sia uguale a un predefinito  diverso da zero,

 cioè  per verificare l’ipotesi nulla

,

 è fondato sulla statistica

 

 dove

 

la varianza è:

 

Anche in questo caso si rifiuta l’ipotesi nulla per valori di  maggiori dei valori critici riportati nelle tavole della distribuzione normale standardizzata.

 

 

I PARADOSSI DELLA STATISTICA KAPPA

Nel 1990 Feinstein e Cicchetti hanno pubblicato due articoli sul Journal of Clinical Epidemiology (Feinstein and Cicchetti, 1990; Cicchetti and Feinstein, 1990) nei quali è proposta una trattazione relativa alla definizione e alle possibili soluzioni di due paradossi della statistica kappa per variabili dicotomiche. Si tratta di due casi in cui la statistica kappa fornisce valori che non sembrano ben interpretare il reale livello di accordo.

Prima di introdurre la definizione dei paradossi, così come è stata proposta dai due autori, ci soffermiamo su alcuni concetti, relativi alle distribuzioni marginali, che stanno a fondamento dei paradossi stessi.

 

-  Bilanciamento e sbilanciamento

Sono situazioni che si verificano a carico di ciascuna delle distribuzioni marginali prese singolarmente. Riscontriamo una situazione di bilanciamento quando i soggetti da valutare si equidistribuiscono nelle due categorie, come nell’esempio in tabella 1.

Quando, invece, vi è prevalenza di una delle due categorie allora si riscontra una situazione di sbilanciamento,  come nell’esempio in tabella 2.

 

Tabella 1: situazione di bilanciamento.

 

 

 

Tabella 2: situazione di sbilanciamento.

 

 

 

 

-  Sbilanciamento simmetrico e asimmetrico

Confrontando lo sbilanciamento delle distribuzioni marginali dei due valutatori si può giudicare uno sbilanciamento simmetrico o asimmetrico rispetto alla diagonale principale.

 

In tabella 3 è riportato un esempio di sbilanciamento simmetrico, caratterizzato dal fatto che lo sbilanciamento delle due marginali ha lo stesso verso. La distribuzione di entrambi gli osservatori è infatti sbilanciata sul “Sì”.

 

In tabella 4 si verifica, invece, una situazione di sbilanciamento asimmetrico in quanto lo sbilanciamento ha verso opposto.

 

 

Tabella 3: sbilanciamento simmetrico.

 

 

 

Tabella 4: sbilanciamento asimmetrico.

 

 

 

 

Notiamo che la situazione di sbilanciamento simmetrico, di per sé, non fornisce alcuna informazione sul livello di concordanza. Tale sbilanciamento, ammesso che non siano stati commessi errori sistematici (di selezione o di classificazione), è semplicemente l’espressione dello sbilanciamento della distribuzione nella popolazione oggetto di studio.

Lo sbilanciamento asimmetrico invece ci fornisce un’informazione di non-accordo che si esprime già sulle frequenze marginali.

 

-  Definizione dei paradossi

Vediamo ora come vengono definiti i paradossi dai due autori:

1)  primo paradosso: “... un alto valore della proporzione di accordo osservato () può essere paradossalmente alterato dalla correzione per l’accordo atteso per il solo effetto del caso”;

 

Tabella 5: esempio del primo paradosso.

 

 

 

Questa è una situazione che si può verificare nel caso di sbilanciamento simmetrico delle frequenze marginali. In questi casi, proprio a causa dello sbilanciamento, la proporzione di accordo atteso può assumere valori talmente alti che, anche a fronte di una proporzione di accordo osservato alta, si possono ottenere valori di kappa tutt’altro che soddisfacenti.

 

2)  secondo paradosso: “Il valore della statistica kappa sarà più alto con uno sbilanciamento asimmetrico piuttosto che simmetrico nelle distribuzioni marginali…..”

 

Tabella 6:  sbilanciamento simmetrico

 

 

 

 

Tabella 7: sbilanciamento asimmetrico.

 

 

 

Come possiamo notare da queste tabelle a parità di accordo osservato lo sbilanciamento asimmetrico fornisce un valore di kappa maggiore che nel caso di sbilanciamento simmetrico.

 

I paradossi da un punto di vista analitico

Come abbiamo avuto modo di spiegare, la statistica kappa è una misura di accordo in cui il livello di accordo osservato  e il livello di accordo massimo (che nella formula classica viene posto pari a 1) vengono aggiustati per un fattore di correzione .

Il valore assunto da tale fattore, che esprime il livello di accordo atteso per il solo effetto del caso (cioè assumendo criteri di valutazione indipendenti), dipende dalle distribuzioni delle frequenze marginali. A parità di accordo osservato, quindi, il valore della statistica kappa varia in funzione del valore di accordo atteso e, indirettamente, in funzione delle distribuzioni marginali.

 

Dal punto di vista formale ciò può essere spiegato esprimendo il valore dell’accordo atteso nel seguente modo:

 dove:

           e           .

 

 

Il valore dell’accordo atteso dipende, quindi, da

-  una quantità fissa che esprime il valore assunto da  in caso di bilanciamento (0.5)

-  e dalla quantità  che esprime lo scostamento dalla situazione di bilanciamento.

In particolare la quantità  assumerà valori positivi nei casi di sbilanciamento simmetrico e valori negativi nei casi di sbilanciamento asimmetrico producendo rispettivamente un abbassamento e un innalzamento dei valori assunti dalla statistica kappa.

 

In figura 1 presentiamo l’andamento dei valori assunti dalla proporzione di accordo atteso () in funzione della quantità  nel caso di perfetto sbilanciamento asimmetrico e simmetrico.

 

Chiariamo che per sbilanciamento perfetto si intende il caso in cui il grado di sbilanciamento sia uguale nelle due marginali.

 

 

 

Questo grafico mostra come si modifica il valore dell’accordo atteso () in funzione della situazione di bilanciamento o sbilanciamento delle marginali. Il valore minimo lo si riscontra nel caso di estremo sbilanciamento asimmetrico perfetto. Man mano che si procede verso una situazione di bilanciamento il valore aumenta fino ad arrivare alla situazione di perfetto bilanciamento in cui . Dopodiché continua a incrementare man mano che si procede verso uno sbilanciamento simmetrico fino ad arrivare al valore massimo in corrispondenza della situazione di estremo sbilanciamento simmetrico perfetto.

 

I paradossi da un punto di vista empirico

Nel caso del primo paradosso, che come abbiamo detto coincide con il caso di sbilanciamento simmetrico, il valore della proporzione di accordo atteso assume valori elevati proprio per effetto dello sbilanciamento. Da un punto di vista empirico questo potrebbe essere spiegato notando che, sempre per effetto dello sbilanciamento, una parte della casistica deve necessariamente collocarsi nella cella di concordanza della categoria di prevalenza.

 

Riprendiamo il nostro esempio.

 

 

 

 

In questa tabella, al fine di rispettare i valori assunti dalle frequenze marginali, nella cella di concordanza del “Sì” devono collocarsi necessariamente almeno 60 casi. Questo implica, da una parte che il valore della proporzione di accordo osservato non potrebbe mai scendere al di sotto di 0.60, dall’altra che questi 60 casi non rappresentano l’effetto di una situazione di concordanza tra i valutatori, ma solo l’effetto dello sbilanciamento della variabile nella popolazione. E maggiore è lo sbilanciamento, maggiore è la proporzione della casistica “non utile” alla valutazione del reale livello di accordo. Risulta quindi corretto che il valore dell’accordo atteso, che nella statistica kappa ha proprio la funzione di “correggere” per tener conto di questa situazione, risulti, in casi come questo, elevato. Il basso valore assunto dalla statistica kappa nel nostro esempio non è quindi da considerarsi paradossale se non apparentemente. Se proviamo, infatti, a considerare la nostra tabella, escludendo i 60 casi di cui sopra, vedremo che il livello reale di accordo è basso e è quindi ben rappresentato dalla stima. Come del resto, un valore elevato dell’accordo atteso, non impedisce alla statistica di assumere valori soddisfacenti nei casi di reale accordo.

Tuttavia, in conseguenza del fatto che la casistica “utile” per la valutazione della concordanza si riduce a una parte della casistica, è sufficiente che anche solo pochi casi si collochino sulle celle di discordanza per portare a un valore di kappa basso.

 

Alla luce di quanto detto potremmo concludere che i valori della kappa in questa situazione sono valori solo apparentemente paradossali, tuttavia, il primo paradosso identifica una situazione delicata di cui è bene tenere presente in fase di pianificazione.

 

In particolare:

-  In fase di pianificazione di uno studio di concordanza su variabili dicotomiche, ove sia possibile, è utile impostare lo studio in modo tale che la variabile sia bilanciata.

-  Ove non fosse possibile selezionare la casistica in modo tale da ottenere variabili bilanciate è consigliabile aumentare la numerosità della casistica stessa in modo tale che le stime siano maggiormente stabili.

 

Il secondo paradosso, al contrario del primo, è da considerarsi reale.

Infatti, non sembra corretto che, a parità di accordo osservato, uno sbilanciamento asimmetrico, che di per se stesso è già indice di disaccordo, produca valori di k più elevati che nel caso di sbilanciamento simmetrico. Come abbiamo avuto modo di spiegare (vedi figura 1), le situazioni di sbilanciamento asimmetrico sono caratterizzate da valori di . Si potrebbe dunque proporre, per ovviare almeno in parte a questo paradosso, di forzare la proporzione di accordo atteso a non assumere valori inferiori a 0.5. Tuttavia, l’effetto di questo paradosso sul valore della statistica è di entità talmente contenuta da non modificare sostanzialmente il giudizio sul grado di concordanza. E’ bene, però, tener presente in fase di interpretazione dei risultati che nel caso di sbilanciamento asimmetrico il valore della statistica kappa risulta essere lievemente sovrastimato. 

 

 APPLICAZIONE

Il presente lavoro è stato pubblicato insieme con altri autori (Corletto V et al, 1998) sull’Analitycal Cellular Pathology. Si tratta di un lavoro nel quale è stato indagato il livello di concordanza, nella valutazione del residuo tumorale su un campione di vetrini, tra l’anatomo-patologo e un analizzatore d’immagine.

All’epoca della pubblicazione di questo articolo veniva proposto, come parte integrante del trattamento primario del tumore della mammella, l’utilizzo della chemioterapia pre-operatoria da effettuarsi, nel caso di tumori di piccole dimensioni, al fine di ridurre il rischio di recidiva locale, e nei tumori di maggiori dimensioni al fine di permettere una chirurgia più conservativa. Uno degli end-point di efficacia era fornito dalla quantità di residuo tumorale che veniva solitamente valutato dall’anatomo‑patologo. Successivamente si è reso disponibile un analizzatore d’immagine che poteva fornire tale valutazione e si è reso quindi necessario valutare la concordanza.

La variabile esprime la classificazione in 4 categorie della presenza di residuo tumorale, in percentuale.

Di seguito riportiamo le tabelle di presentazione dei dati e dell’analisi statistica.

 

 

 

Tabella 3: Valori della kappa e intervalli di confidenza al 95% per la kappa classica e per la kappa pesata.

 

 

 

ESEMPIO*

*Realizzato utilizzando il software SAS di proprietà esclusiva, tutelata dalla normativa sui diritti d'autore, di SAS Institute Inc., Cary ,North Carolina, USA.

 

ISTRUZIONE

*======================================RIPRODUCIBILITA’;

data riprod;

input AP1 AP2 wt;

cards;

1 1 11

1 2 3

1 3 0

1 4 0

2 1 0

2 2 6

2 3 3

2 4 0

3 1 1

3 2 1

3 3 25

3 4 0

4 1 0

4 2 0

4 3 1

4 4 18

;

 

proc freq order=data;

weight wt;

 

table AP1*AP2/agree (wt=FC) printkwt nopct norow nocol;

      exact kappa wtkap;

  run;

 

 

OUTPUT

TABLE OF AP1 BY AP2

AP1       AP2

 

 Frequency|    1   |    2   |    3   |    4   |  Total

 ---------+--------+--------+--------+--------+

      1   |   11   |    3   |    0   |    0   |     14

 ---------+--------+--------+--------+--------+

      2   |    0   |    6   |    3   |    0   |      9

 ---------+--------+--------+--------+--------+

      3   |    1   |    1   |   25   |    0   |     27

 ---------+--------+--------+--------+--------+

      4   |    0   |    0   |    1   |   18   |     19

 ---------+--------+--------+--------+--------+

 Total        12       10       29       18         69

 

 Simple Kappa Coefficient

 --------------------------------

 Kappa (K)                 0.8162

 ASE                       0.0563

 95% Lower Conf Limit      0.7059

 95% Upper Conf Limit      0.9265

 

 Test of H0: Kappa = 0

 ASE under H0              0.0729

 Z                        11.2026

 One-sided Pr >  Z         <.0001

 Two-sided Pr > |Z|        <.0001

                                

 Kappa Coefficient Weights(Fleiss-Cohen Form)

  AP2        1           2           3           4

 ---------------------------------------------------

   1      1.0000      0.8889      0.5556      0.0000

   2      0.8889      1.0000      0.8889      0.5556

   3      0.5556      0.8889      1.0000      0.8889

   4      0.0000      0.5556      0.8889      1.0000

 

 Weighted Kappa Coefficient

 --------------------------------

 Weighted Kappa (K)        0.9209

 ASE                       0.0321

 95% Lower Conf Limit      0.8579

 95% Upper Conf Limit      0.9838

 

 Test of H0: Weighted Kappa = 0

 ASE under H0              0.1202

 Z                         7.6605

 One-sided Pr >  Z         <.0001

 Two-sided Pr > |Z|        <.0001