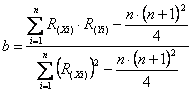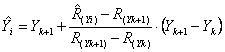TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.16.    LA REGRESSIONE MONOTONICA DI IMAN-CONOVER

 

 

In una distribuzione bivariata, nella quale

-  una variabile è identificata con la causa e è detta variabile indipendente, indicata con X,

-  l’altra è identificata con l’effetto e è detta variabile dipendente, indicata con Y,

 può sorgere il problema di verificare se al crescere della prima variabile la seconda cresce o diminuisce, senza richiedere che il rapporto sia di tipo lineare, cioè costante.

E’ la regressione monotonica.

 

Tra i metodi presenti in letteratura, quello proposto da R. L. Iman e W. J. Conover nel 1979 (vedi The use of the rank transform in regression su pubblicato su Technometrics vol. 21 pp. 499-509) è il più diffuso; inoltre, è presentato nel testo di Conover del 1999 (Practical Nonparametric Statistics, 3^rd ed. John Wiley & Sons, New York, 584 p.), indubbiamnete da annoverare tra quelli internazionali più noti.

 

Da esso è tratto l’esempio seguente, qui illustrato con una presentazione più dettagliata della metodologia, una esposizione  di tutti i passaggi logici e con la correzione di alcuni risultati.

 

 

 

 

La teoria sottostante a tale approccio, già presentato nel paragrafo dedicato alla correlazione non parametrica, è che

-  quando tra i ranghi di due variabili esiste regressione lineare,

-  tra i loro valori osservati (su scale ad intervalli o di rapporti) esiste regressione monotonica.

Di conseguenza, è utile calcolare la retta di regressione lineare sui ranghi e la sua significatività. Per questo ultimo test, cioè per valutare l’ipotesi nulla H₀: b = 0 si ritorna alla correlazione non parametrica già illustrata, per un concetto del tutto analogo alla verifica della regressione lineare di Theil.

 

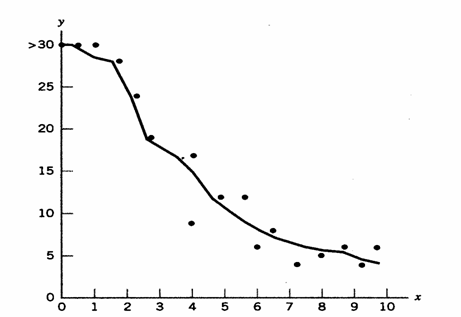
Per valutare se l’aggiunta di zucchero al mosto d’uva favorisce la fermentazione, in 17 esperimenti indipendenti alla stessa quantità di mosto è stata aggiunta una quantità differente di zucchero (X, misurata in libbre); successivamente per 30 giorni è stato valutato se la fermentazione era iniziata (Y, misurata in giorni trascorsi). Dopo 30 giorni l’esperimento è stato interrotto. Nei tre contenitori ai quali erano state aggiunte le quantità di zucchero minori (cioè X uguale a 0,0;  0,5;  1,0 libbre) la fermentazione non era ancora iniziata: a essi è stata attribuita la misura approssimata Y >30.

 

Curva di regressione monotonica con i dati osservati

 

 

I dati dei 17 campioni indipendenti (individuati nella colonna 1 dalle lettere da A a S) sono riportati nelle colonne 2 () e 3 () della tabella precedente. Nel grafico sottostante, sono rappresentati i punti () che identificano le 17 osservazioni (i segmenti che descrivono la tendenza sono spiegati nella parte finale del paragrafo).

 

Il metodo di Iman-Conover richiede due serie di passaggi:

-  la prima per calcolare la retta di regressione sui ranghi dei valori;

-  la seconda per ritornare da questa retta ai valori originali, trasformadola in una serie di segmenti che descrivono la regrassione monotonica di Y su X, nella scala effettivamente utilizzata.

 

Questi passaggi logici e metodologici sono:

1 - Trasformare i valori della variabile X e Y (riportati nelle colonne 2 e 3 della tabella precedente) nei loro ranghi (come nelle colonne 4 e 5).

 

Il grafico sottostante, come evidenzia anche la differente scala riportata in ascissa e in ordinata, è la rappresentazione dei punti mediante i loro ranghi.

 

RETTA DI REGRESSIONE OTTENUTA CON LA TRASFORMAZIONE DEI DATI IN RANGHI

 

 

2 – Calcolare la retta sui ranghi (quella rappresentata nella figura). Dapprima si stima il coefficiente angolare  con

 

 una formula corrispondente a quella abbreviata della retta parametrica.

Utilizzando i dati dell’esempio, dove

-  = 996,5  (colonna 6)

-  = 1784,5  (colonna 7)

-    = 17

 

 

 si ottiene il coefficiente angolare  = -0,935.

 Successivamente, si stima l’intercetta  con

 

 

 Utilizzando i dati dell’esempio

 

 

 risulta  = 17,415.

Di conseguenza, la retta di regressione stimata mediante i ranghi è

 

 

 

3 – Questa formula permette di calcolare i valori attesi per ogni rango di Y a partire dai ranghi di X, cioè gli  riportati nella colonna 8, anche se per tracciare la retta è sufficiente calcolarne solo due.

Ad esempio,

-  per il campione A con  = 0,0  e  quindi rango  = 1 si ottiene la stima del rango di Y

 

-  per i campioni G e H  con  = 4,0  e  rango  = 7,5 si ottiene la stima del rango di Y

 

La retta è costruita con i punti (), cioè utilizzando i dati della colonna 4 e quelli riportati nella colonna 8.

 

4 – Per valutare la significatità della retta così calcolata (H₀: b = 0), quindi se esiste regressione monotonica sui dati originali, è sufficiente valutare la significatività della correlazione non parametrica (H₀: r = 0); può essere ottenuta  indifferentemente con il test r di Spearman oppure con il t di Kendall.

 

 

5 - Dalla retta calcolata sui ranghi, si ritorna alla scala originale di X e Y calcolando gli  riportati nella colonne 9. Unendo i punti individuti dai valori  osservati della colonna 1 e quelli  stimati riportati nella colonna 9 (cioè i punti , si ottiene la linea spezzata, rappresentata nella prima figura.

 

 

6 - Per identificare tutti i valori  di questa regressione monotonica, la procedura è complessa e richiede alcune scelte, che dipendono dal valore ottenuto del rango stimato per Y (cioè  della colonna 8):

a)       se  è uguale al rango reale della stessa osservazione Y, cioè  della colonna 5,  si attribuisce a  il valore osservato ;

b)       se  è compreso tra il rango di due osservazioni adiacenti di Y, cioè  e  della colonna 3, con  minore in valore di ,  per ottenere il valore stimato di Y, cioè  della colonna 9, si usa l’interpolazione

 

 

c)        se  è minore del rango osservato  più piccolo (colonna 4), il valore stimato di Y (cioè  della colonna 9) è uguale a quel valore osservato minore;

d)       se   è maggiore del rango osservato  più grande (colonna 4), il valore stimato di Y (cioè  della colonna 9) è uguale a quel valore osservato  maggiore.

 

Ad esempio,

-          per il campione A il valore stimato del rango è  = 16,48 (colonna 8); poiché è maggiore del rango più grande (= 16 di colonna 4) , il valore stimato di Y è  >30;

-          per il campione B il valore stimato del suo rango è  = 15,55 (colonna 8); è compreso tra il rango 16 e il rango 14; quindi

-          per il campione C

 

-          per il campione D

 

-          per il campione E

 

-          per il campione F

 

-          per il campione G

 

I valori stimati sono riportati nella colonna 9 (gli altri sono ripresi da Conover).

Nell’esempio utilizzato, tre valori sono molto approssimati (>30) e tra loro identici, quindi che introducono bias nei calcoli. Il metodo dimostra di essere abbastanza robusto da riuscire ugualmente a fornire stime della regressione monotonica. Tuttavia, lo stesso Conover raccomanda di usare scale continue, quindi definite con precisione e senza valori identici