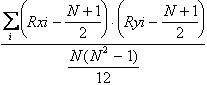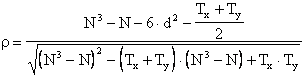TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.1.  LA CORRELAZIONE NON PARAMETRICA  (rho) DI SPEARMAN, CON LA DISTRIBUZIONE DI Hotelling-Pabst.

 

 

La correlazione è uno dei metodi statistici più antichi, diffuso già all’inizio del ‘900, almeno dieci anni prima del test t di Student e quasi trenta prima dell'analisi della varianza. La metodologia non parametrica proposto da

-  C. Spearman nel 1904 (con l’articolo The proof and measurement of association between two things su American Journal of Psychology vol. 15, pp. 72 – 101 e con l’articolo A footrule for measuring correlation , pubblicato nel 1906 su Brit. Journ. Psychol. n. 2)

 è una correlazione basata sui ranghi, che ricorre agli stessi concetti della correlazione parametrica r di Pearson presentata anch'essa poco prima, nel 1900, e successivamente chiamata Pearson’s Product Moment Sample Correlation Coefficient.

Questa metodologia non parametrica ha subito varie elaborazioni e modifiche. Era ancora discussa negli anni ‘20, come può dimostrare l’articolo di W. S. Gosset (Student) del 1921 An experimental determination of the probable error of Dr. Spearman’s correlation coefficients (comparso su Biometrika vol. 13). Ora, dopo un secolo, è ancora uno dei test più ampiamente utilizzati, per lo studio dell'associazione tra due variabili quantitative.

 

In riferimento ai test di correlazione non parametrica, in letteratura sono ricorrenti i termini di correlazione tra ranghi, cograduazione, associazione e concordanza. Da molti utenti della statistica, sono usati come sinonimi; ma

-  i primi due (correlazione e cograduazione) dovrebbero essere utilizzati in modo appropriato solo con scale almeno di tipo ordinale,

-  mentre le ultime due (associazione e concordanza) con scale qualitative o categoriali.

Il coefficiente di correlazione di Spearman è sovente indicato con il simbolo greco  (rho);  in altri testi è simboleggiato con r_S, per evidenziare la sua affinità con il test r di Pearson dal quale è derivato. Come esso, può variare

-  tra +1 e –1 quando la correlazione è massima, con valore positivo oppure negativo;

-  è vicino a zero, quando non esiste correlazione.

 

Il metodo richiede che entrambe le variabili siano misurate su una scala almeno ordinale, per cui ognuna delle due serie di misure, indicate sovente con X e Y anche se non esiste tra esse una relazione di causa effetto e dovrebbero essere correttamente indicate con X₁ e X₂, non dovrebbe avere valori uguali entro la stessa sequenza. Questo metodo può essere più potente del test r di Pearson anche per scale d'intervallo o di rapporto, quando le condizioni di validità del test parametrico non sono pienamente soddisfatte. Di conseguenza, come per altri test non parametrici, la sua utilizzazione è consigliabile insieme con il test parametrico, ad ulteriore dimostrazione e verifica delle conclusioni raggiunte. In particolare quando si disponga solo di pochi dati e pertanto non sia possibile dimostrare che le condizioni di validità del test parametrico sono soddisfatte in modo completo.

 

Il coefficiente di correlazione per ranghi di Spearman serve per verificare l'ipotesi nulla dell'indipendenza tra due variabili, nel senso che gli N valori della variabile Y hanno le stesse probabilità di associarsi con ognuno degli N valori di X.

L’ipotesi alternativa di esistenza di una associazione può prevedere un risultato positivo oppure negativo. Nel primo caso è detta associazione diretta: le coppie di valori sono contemporaneamente alti o bassi sia per X che per Y; nel secondo caso, chiamata anche associazione indiretta, a valori alti di X corrispondono valori bassi di Y o viceversa.

Per una illustrazione didattica chiara, i vari passaggi logici richiesti dal metodo proposto da Spearman possono essere suddivisi in 5 fasi, di seguito presentate nella dimostrazione di un caso.

e

-  sia bilaterale

H₀: r = 0       contro        H₁: r ¹ 0

 

-  sia unilaterale in una direzione

H₀: r £ 0      contro      H₁: r > 0

 oppure nell’altra

H₀: r ³ 0      contro      H₁: r < 0

 è utile riportare i dati come nella tabella seguente

 

 

2 - Successivamente, occorre ordinare i ranghi della variabile X, assegnando 1 al valore più piccolo e progressivamente valori interi maggiori, fino ad N per il valore più alto.

Se i dati della variabile X hanno due o più valori uguali, è necessario assegnare ad ognuno di essi come rango la media delle loro posizioni.

 

 

Anche se ininfluente ai fini dei calcoli successivi, è utile alla comprensione della misura di correlazione porre nell'ordine naturale (da 1 a N) i ranghi della variabile X e spostare la collocazione dei valori di Y relativi al medesimo soggetto, come nella tabella sovrastante.

 

3 - Sostituire anche gli N valori di Y con i ranghi rispettivi; per valori di Y uguali, usare la media dei loro ranghi:

 

 

 

Si ottiene la riga Y, riportata in grassetto.

 

4 - Se le due distribuzioni (quella della serie delle X e quella della serie delle Y)

-  sono correlate in modo positivo (r = +1),  i valori della variabile X e della Y relativi allo stesso soggetto saranno uguali;

-  sono correlate in modo negativo (r = -1), a valori alti di X saranno associati valori bassi di Y e viceversa;

-  se tra le due variabili non esiste correlazione (r = 0), i valori di X e di Y relativi agli stessi soggetti saranno associati in modo casuale.

 

Per quantificare questo grado di correlazione o concordanza, Spearman ha proposto la distanza tra le coppie dei ranghi ()

 

 

 come calcolate nella terza riga (R_i); successivamente devono essere elevate al quadrato come riportate nella quarta riga (R²_i)

L’indicatore di correlazione, da cui derivano i passaggi logici e metodologici successivi, è la somma di questi quadrati:

Con i dati dell’esempio, la somma delle d²_Ri è uguale a 10 (1 + 1 + 1 + 1 + 4 + 1 + 1 = 10)

 

5 - Quando r = +1, le coppie di osservazioni di X e Y hanno lo stesso rango e pertanto questa sommatoria è uguale a 0.

Quando r = -1, se X è ordinato in modo crescente, Y è ordinato in modo decrescente: di conseguenza, le differenze sono massime e la sommatoria raggiunge un valore massimo determinato dal numero di coppie di osservazioni (N).

Quando r = 0, mentre i ranghi di X sono ordinati in modo crescente quelli di Y hanno una distribuzione casuale: la sommatoria delle  tende ad un valore medio, determinato dal numero di coppie di osservazioni (N).

 

Il test è fondato sulla statistica

D =

 ed è conosciuto anche come test statistico di Hotelling-Pabst (vedi l’articolo di H. Hotelling e M. R. Pabst del 1936 Rank correlation and tests of significance involving no assumption of normality, in Annals of Mathematical Statistics, Vol. 7, pp. 429-443).

Per essa sono state proposte tavole di valori critici, al fine di valutare la significatività del test.

 

6 - Il coefficiente di correlazione tra ranghi (r) di Spearman è derivato dalla formula della correlazione di Pearson

Applicata ai ranghi, dopo semplificazione diviene

 

r =

 

Il coefficiente di correlazione per ranghi di Spearman è semplicemente il coefficiente di correlazione di Pearson applicato ai ranghi.

Ritornando alla somma degli scarti tra i ranghi, 

 la formula abbreviata può essere scritta come

 con N uguale al numero di coppie di osservazioni.

In vari testi, è scritto con la formula equivalente

 

Quando due o più valori di X o di Y sono identici (ties) e pertanto hanno lo stesso rango, l'attribuzione dei punteggi medi riduce il valore della devianza. Con pochi valori identici, l'effetto è trascurabile. Con molti valori identici, è bene calcolare un fattore di correzione T sia per la variabile X () sia per la Y ()

 dove

g   è il numero di raggruppamenti con punteggi identici e

 t   è il numero di ranghi identici entro ogni raggruppamento.

 

Con queste correzioni, nel caso di molti valori identici la formula completa del  di Spearman

 diventa

 

 

Come in tutti i ties e già evidenziato, la correzione determina

-  una differenza sensibile quando uno stesso valore è uguale in molti casi,

-  un effetto trascurabile o comunque ridotto quando si hanno molti valori ripetuti solo 2 volte.

Di conseguenza, nonostante la correzione, questo test è da evitare e può essere utile ricorrere ad altri metodi, quando uno o più valori sono ripetuti con frequenza elevata, nella X e/o nella Y.

 

Nel caso di piccoli campioni (N < 20-25), la significatività di  è fornita dalle tabelle dei valori critici. Nella pagina successiva sono riportati i valori critici di r, sia per test a una coda che per test a due code.

Alla probabilità a prefissata, si rifiuta l’ipotesi nulla se il valore calcolato è uguale o superiore a quello riportato nella tabella.

 

Nel caso di grandi campioni (N > 20-25), quando è valida l'ipotesi nulla d'assenza di correlazione, il valore di  è distribuito con media 0 e deviazione standard 1. Per la sua significatività è stato proposto

-  sia il ricorso alla distribuzione Z con la trasformazione

 

 

-  sia alla distribuzione t di Student con gdl N - 2 con la trasformazione di r

 

 

Tra t e Z,

-  il test t sembra preferibile, in quanto giustamente più cautelativo ma pertanto meno potente, quando il campione ha meno di 50 osservazioni;

-  per campioni di dimensioni maggiori, i due metodi risultano equivalenti poiché i valori critici  sono quasi coincidenti,

- non diversamente da quanto avviene per il confronto tra due medie.

 

Valori critici del coefficiente r di Spearman

per test a 1 coda (1^a riga) e test a 2 code (2^a riga)

a

 

ESEMPIO. La concentrazione delle sostanze organiche presenti nell'acqua può essere misurata mediante il BOD (da Biological Oxygen Demand, la richiesta biochimica dell'ossigeno), il COD (da Chemical Oxygen Demand, la richiesta chimica dell'ossigeno) e il TOC (da Total Organic Carbon, il carbonio organico totale).

Lungo un corso d'acqua sono state fatte 16 rilevazioni del BOD₅ (a 5 giorni) e dell'azoto ammoniacale, con la successiva serie di misure.

 

 

 

 

S’intende verificare se tra le due serie di valori esista una correlazione positiva significativa, nonostante la non normalità delle distribuzioni, come evidenzia la semplice lettura dei dati della stazione S₄.e S₅, ovviamente da confermare con le analisi relative.

 

Risposta.  Il test è unilaterale, con

H₀: r £ 0       contro       H₁: r > 0

 

Il metodo può essere suddiviso in 7 fasi; per le prime 5, qui elencate, i calcoli sono riportati nella tabella successiva:

1 - ordinare in modo crescente i valori del BOD₅ ed attribuire i ranghi relativi (colonne 1a e 1b);

2 - trasformare in ranghi i corrispondenti valori di N (colonne 2a e 2b);

3 - calcolare la differenza  d  tra i ranghi (colonna 3);

4 - elevare al quadrato tali differenze (d² nella colonna 4);

5 - calcolare la somma dei quadrati delle differenze (somma delle d² nella colonna 4);

Con i dati dell’esempio, ( ) è uguale a 220,5.

6 - Per N uguale a 16, calcolare il valore di r

 

 

 che risulta uguale a 0,676.

 

 

 

 

7 - Nella tabella dei valori critici, alla probabilità a = 0.01 per un test a 1 coda il valore riportato è 0.582. Il valore calcolato è superiore: si rifiuta l’ipotesi nulla e si accetta implicitamente l'ipotesi alternativa dell'esistenza di un’associazione positiva tra le due serie di dati rilevati.

Benché il numero di dati (N = 16) sia oggettivamente ridotto, la significatività può essere stimata sia con  la distribuzione Z che  con la distribuzione t di Student.

 

Con il test  Z  si ottiene

 un valore di Z uguale a 2,62.

Nella tabella della distribuzione normale unilaterale, a

-   Z = 2,62 corrisponde la probabilità a = 0.0044.

 

L'approssimazione con il risultato precedente è molto buona: con tabelle di r più dettagliate e ovviamente all’aumentare del numero di osservazioni, la differenza risulta trascurabile; in questo caso è di circa il 2/1000.

 

Con il test t si ottiene

 

 

 

 un valore di t uguale a 3,433 con 15 gdl.

 

Nella tabella sinottica dei valori critici del t di Student per un test unilaterale,

-   =3,433 si trova tra la probabilità a = 0.005 (t₁₅ = 2,947)  e  a = 0.0005 (t₁₅ = 4,073).

 

La conclusione non è molto differente da quella ottenuta con i due metodi precedenti.

I tre risultati sono approssimativamente equivalenti.

 

Un altro esempio di correlazione con il test r_s di Spearman è riportato nel successivo paragrafo  dedicato al test di Daniels.

 

Sono stati proposti anche altri metodi, per stimare la significatività della regressione non parametrica r di Spearman. Tra i testi a maggior diffusione, quello di

-  W. J. Conover del 1999 (Practical nonparametric statistics, 3^rd ed. John Wiley & Soons, New York, 584) riporta i valori critici dei quantili, esatti quando X e Y sono indipendenti,

-  calcolati da G. J. Glasser e R. F. Winter nel 1961 (nell’articolo Critical values of the coefficient of rank correlation for testing  the hypothesis of indipendence, pubblicato su Biometrika Vol. 48, pp. 444-448).