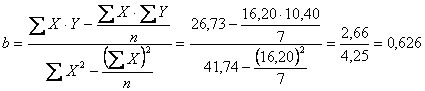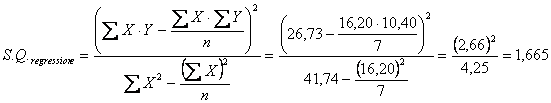TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

 

21.6.   SIGNIFICATIVITA’ DELLA REGRESSIONE E DELLA CORRELAZIONE LINEARE PARAMETRICA CON I TEST NONPARAMETRICI r  E t.

 

 

Nei paragrafi dedicati alla regressione lineare parametrica, è stato discusso come la verifica dell’ipotesi nulla sulla linearità con

H₀:  b = 0

 attraverso la significatività del valore r di correlazione, per il quale l’ipotesi nulla è

H₀ : r = 0

 sia un metodo concettualmente errato, anche se conduce alla stima di una probabilità a identica a quella ottenuta con il test che utilizza il valore del coefficiente angolare b.

 

I motivi fondamentali evidenziati, a causa dei quali i testi non confondano mai le due procedure, sono

-  la diversa ipotesi che i test per la regressione e quelli per la correlazione verificano e

-  le differenze nelle condizioni di validità.

 

Quando uno o più punti sono anomali e quindi la distribuzione dei dati è fortemente asimmetrica, una condizione di non validità della regressione lineare che è frequente nella pratica sperimentale, questi due metodi parametrici (che forniscono risultati di a coincidenti) spesso risultano significativi. Ma dimostrare che i dati non sono distribuiti in modo normale neppure approssimativamente, quindi che l’analisi condotta non è attendibile, non è semplice; in particolare, è quasi impossibile rifiutare l’ipotesi nulla sulla normalità, quando i dati sono pochi.

Un metodo pratico e semplice di tale verifica può essere l’uso della correlazione lineare non parametrica.

 

Questi concetti possono essere espressi con termini più rigorosi:

-  la funzione di distribuzione del test parametrico r di Pearson dipende dalla funzione di distribuzione bivariata, cioè della X e della Y, mentre i test non parametrici per l’analisi della correlazione sono indipendenti da essi.

 

La verifica della validità della regressione e della correlazione lineare, seppure calcolate con metodi parametrici, può quindi essere fornita dalla correlazione non parametrica. Se la risposta della correlazione non parametrica è significativa o vicina alla probabilità del test parametrico, il risultato di questo ultimo può essere ritenuto corretto. In caso contrario, quando il test di correlazione non parametrica non risulta significativo, si può dedurre che facilmente il test parametrico è stato applicato senza rispettare la condizione di normalità della distribuzione dei dati.

 

 

Dopo aver calcolato le quantità necessarie alle stime successive

                        

            

 come evidenziato nella tabella per gli ultimi tre

 

 

 

 

 

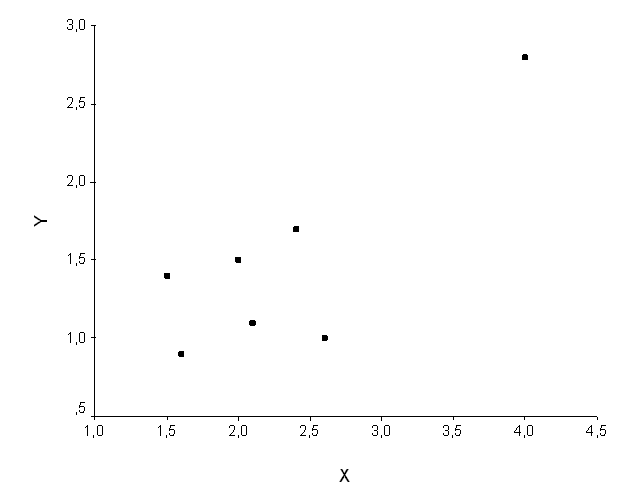
A dimostrazione empirica di questa procedura sperimentale, si assuma di voler calcolare il coefficiente di regressione lineare semplice, per la seguente serie di dati bivariati:

 

 

 

 

La sua rappresentazione grafica evidenzia visivamente la presenza di un punto anomalo: un valore di X nettamente più alto degli altri, associato ad un valore di Y ugualmente elevato e distante dalla distribuzione di tutti gli altri punti.

 

Dai dati sperimentali, dopo aver calcolato le quantità

 

 

 

 si ricava il valore di b

 

 

 e successivamente il valore di a

 

Infine, si scrive la retta

 

Per testare l’esistenza di una relazione lineare tra X e Y con ipotesi bilaterale, cioè per verificare l’ipotesi bilaterale

H₀: b = 0      contro      H₁: b ¹ 0

 

1-   dopo aver calcolato la devianza totale

 

 

2 - la devianza dovuta alla regressione

 

 

 è possibile costruire la tabella dell’ANOVA

 

 

 

 

 completando i dati relativi alla devianza e ai df dell’errore con la proprietà additiva.

 

Il test F

 stima F = 9,85 con df 1 e 5.

Poiché il valore critico per un test bilaterale alla probabilità a = 0.05 è uguale a 10,0 e il valore calcolato è leggermente minore (9,85),a causa del numero limitato di dati si può affermare che il test è tendenzialmente significativo.

 

L’analisi della correlazione parametrica r di Pearson conduce alle stesse conclusioni.

Dal valore di R², ricavato per semplicità e in modo rapido dal rapporto tra le devianze,

 

 si ottiene facilmente  quello di r

 

Per verificare la significatività dell’ipotesi bilaterale

H₀: r = 0      contro      H₁: r ¹ 0

 si può utilizzare il test F

 

 che ovviamente fornisce lo stesso identico risultato della regressione lineare, a meno delle approssimazioni introdotte nel calcolo come numero di decimali; quindi determina la stessa probabilità a, essendo sempre un valore di F con gdl 1 e 5.

 

Questa stessa ipotesi

H₀: r = 0      contro      H₁: r ¹ 0

 e implicitamente quella sulla regressione lineare possono essere verificate mediante la correlazione non parametrica.

Con i ranghi

 

 

 

 secondo il metodo di Spearman si ricava

 

 

 la stima r = 0,429. E’ un risultato molto lontano dalla significatività. Infatti nella tabella dei valori critici per un test bilaterale con df = 5  e  a = 0.10 il valore critico è r = 0,900.

 

Il confronto tra due risultati così differenti, quello della probabilità a stimata con un metodo parametrico e quella della probabilità a ottenuta mediante la correlazione non parametrica, permette di dedurre che la significatività ottenuta con il test parametrico è del tutto imputabile alla presenza di un valore anomalo; di conseguenza, in realtà tale regressione lineare non esiste.

Non esiste una regressione lineare tra i ranghi e quindi non può esistere nemmeno tra i valori osservati

Applicando il test t di Kendall invece del test r di Spearman si perviene alle stesse conclusioni.