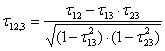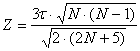TEST NON PARAMETRICI

PER CORRELAZIONE, CONCORDANZA,

REGRESSIONE MONOTONICA E REGRESSIONE LINEARE

 

 

21.7.  IL COEFFICIENTE DI CORRELAZIONE PARZIALE: _12,3 DI KENDALL, r_12,3 DI SPEARMAN

 

 

Quando si analizza la correlazione tra 2 variabili, in varie occasioni può sorgere il dubbio che la causa principale di un valore elevato, non importa se positivo o negativo, possa essere attribuita non ad una correlazione effettiva tra loro,

-  ma ad una correlazione o associazione di ognuna con una terza variabile.

 

Può anche succedere il fenomeno opposto.

L’inatteso basso valore di correlazione tra due variabili, che notoriamente sono tra loro correlate in modo positivo

-  sia imputabile all’azione di segno opposto di una terza variabile, alla quale entrambe sono correlate.

 

Come già discusso nel caso della correlazione parametrica, gli effetti delle variazioni congiunte tra due variabili dovute al loro legame con una terza possono essere eliminati, quando si tenga costante quest'ultima; ma è un procedimento e che limita le conclusioni a quel caso specifico. Non è detto che, per altri valori della terza variabile, le prime due mantengano lo stesso grado di correlazione calcolata per alcuni. Analizzare tutti i casi possibili richiede molto tempo. E’ un caso frequente nella ricerca ambientale, biologica e farmacologica, che sovente utilizzano le correlazioni statistiche come indicazione preliminare e come supporto all’indagine causale.

 

Le sostanze contaminanti rilasciate in fiumi e laghi determinano effetti nocivi sulle popolazioni sia animali sia vegetali e sulle comunità acquatiche. Gli effetti principali possono essere raggruppati in alcune categorie: eutrofizzanti, deossigenanti, tossici, fisici come quelli sulla temperatura, chimici come quelli sul pH, patogeni.

Temperatura, eutrofizzazione e deossigenazione risultano tra loro correlati. Per misurare in modo corretto la relazione tra eutrofizzazione e deossigenazione in un gruppo di laghi, occorrerebbe fare rilevazioni a temperatura costante; ma le conclusioni sarebbero limitate a quella specifica temperatura. Nello stesso modo, dovrebbero essere verificate le relazioni sia tra temperatura e deossigenazione con un livello di eutrofizzazione costante, sia le relazioni tra temperatura ed eutrofizzazione con un indice di deossigenazione mantenuto stabile.

Per rendere generali le conclusioni sulla correlazione tra due variabili occorrerebbe un numero molto alto di esperimenti, estesi a tutti i livelli o modalità della terza variabile.

 

La correlazione parziale tra k variabili permette di valutare il grado di correlazione esistente tra ogni coppia di variabili, utilizzando solo una serie di dati. Il caso più semplice e frequente è quello tra 3 variabili, indicate con 1, 2 e 3; ad esso viene limitata la presentazione della correlazione parziale non parametrica  di Kendall, come è già stato fatto con l’indice r di Pearson nel capitolo precedente sulla correlazione parziale parametrica.

Il  (leggesi: valore di correlazione tra le variabili 1 e 2, indipendente da 3) di Kendall

-  misura quanto le misure delle variabili 1 e 2 siano correlate, indipendentemente dal loro accordo con  quelle di 3.

 

La correlazione parziale  può essere derivata dai valori delle 3 correlazioni semplici (t₁₂, t₁₃ e t₂₃), in accordo con la relazione

 

L’applicazione e l’interpretazione sono identiche a quelle della correlazione netta parametrica; di conseguenza, per tali argomenti si rinvia ad essa.

Il test può essere unilaterale oppure bilaterale.

 

Nel primo caso, l’ipotesi nulla H₀ è che non esista correlazione, mentre l’ipotesi alternativa H₁ unilaterale può supporre la presenza di una correlazione sia positiva che negativa, che deve sempre essere chiaramente espressa.

 

Nel secondo caso, l’ipotesi alternativa H₁ bilaterale verifica la semplice presenza di una correlazione, senza alcuna indicazione di segno.

 

Con più variabili, il numero di confronti possibili diventa elevato. Si pone lo stesso problema di significatività già discusso per i confronti tra più medie.

Si ricorre a concetti analoghi al t di Bonferroni per confronti multipli a posteriori, se i confronti non sono già prestabiliti e limitati a quelli ritenuti importanti per la ricerca.

 

La significatività è stimata attraverso gli stessi metodi e gli stessi valori della correlazione semplice.

 

Per piccoli campioni, la significatività è fornita dalla tabella dei valori critici (vedi pagina successiva).

 

Valori  critici  del  coefficiente  di correlazione  parziale  t _12,3  di  Kendall

per test a 1 coda e a 2 code

 

a

 

 

Per grandi campioni, si ricorre alla distribuzione normale, con formula identica a quella della correlazione semplice

dove

-  t è il valore calcolato con la formula presentata per la correlazione netta, cioè t_12,3

-  N è il numero di dati, uguale per tutte le variabili a confronto.

 

Anche il test r di Spearman è stato esteso alle misure di correlazione parziale, nello stesso modo descritto per il t di Kendall. Come già ricordato in altre situazioni, il vantaggio dell’uso del r di Spearman è determinato dal fatto che si ottiene lo stesso risultato dei coefficienti della correlazione parziale r di Pearson, usando i ranghi al posto dei dati.

 

Poiché i programmi informatici per il calcolo dell’indice r di Pearson sono più diffusi di quelli per i test equivalenti non parametrici, è sufficiente questa semplice sostituzione per applicare il test desiderato.

 

Come nella correlazione lineare semplice parametrica e in quella non parametrica, è necessario tenere presente che mentre la distribuzione dei valori parametrici r_12,3 dipende dalla funzione di distribuzione multivariata delle variabili 1, 2 e 3, la distribuzione dei valori non parametrici t_12,3 e r_12,3 sono distribution free, cioè sono indipendenti dalla forma di distribuzione dei dati originari, ma solamente quando le tre variabili considerate sono tra loro mutuamente indipendenti. Sono concetti illustrati da vari studiosi e discussi in particolare da G. Simon in due articoli del 1977; ad essi si rimanda per approfondimenti (il primo: A nonparametric test of total indipendence based on Kendall’s tau, pubblicato su Biometrika Vol. 64, pp. 277-282; il secondo: Multivariate generalization of Kendall’s tau with application to data reduction, pubblicato su Journal of the American Statistical Association Vol. 72, pp. 367 - 376).

 

Kendall ha proposto anche una metodologia utile per stimare direttamente la correlazione netta, servendosi dei dati originari delle tre variabili. Il metodo è lungo e complesso; in pratica, può essere applicato con successo ricorrendo ai calcoli manuali, solo nel caso in cui N sia limitato a poche osservazioni.

 

Per comprendere in modo dettagliato ed operativo questo metodo di Kendall, si supponga di avere misurato tre variabili (X, Y, Z), su un gruppo formato da 5 rilevazioni campionarie, con i seguenti risultati:

 

 

 

 

Calcolare la correlazione parziale o netta (t_YZ,X) tra Y e Z, al netto di X.

 

La metodologia richiede alcuni passaggi:

 

1- La serie dei valori deve essere ordinata in modo crescente per la variabile X (già fatto nella tabella di presentazione dei dati).

 

2 - Trasformare i valori in ranghi, entro ogni variabile, ordinando separatamente i ranghi delle altre due variabili (Y e Z), ma senza spostare la loro collocazione in riferimento alla rilevazione della variabile X.

Con i dati del campione, dopo queste due operazioni si ottiene una nuova tabella:

 

 

 

 

3 - Per ognuna delle 3 variabili, tradurre l'ordine dei ranghi in concordanze e discordanze,

-  assegnando + ad ogni coppia in ordine naturale o crescente e

-  assegnando - ad ogni coppia in ordine non naturale o decrescente;

 ovviamente per la variabile X esistono solo concordanze e quindi segni +

 

 

 

Ad esempio,

per la variabile Y la coppia di ranghi per la coppia I e II è decrescente (3 e 1) e pertanto è stato assegnato -,

 mentre per la variabile Z la stessa coppia di ranghi (2 e 3) è crescente e pertanto è stato assegnato +.

 

4 - Riassumere in una tabella 2 x 2, come quella sottoriportata, l'informazione delle concordanze e delle discordanze delle variabili Y e Z, in relazione all'ordine di X.

Per esempio, nella coppia di rilevazioni I e II,

 il rango della Y (-) è in disaccordo con X,

 mentre quello di Z (+) è in accordo con X.

 

 

 

 

Con i dati dell'esempio, le coppie di rilevazioni sono complessivamente 10, come riportato nella casella contrassegnata dal simbolo N.

Nella casella A, il numero 6 indica che in 6 coppie di rilevazioni (I,IV; I,V; II,IV; II,V; III,V; IV,V) le variabili Y e Z sono tra loro concordanti come con la variabile X; in altri termini, in 6 casi quando si ha il segno + nella colonna X si ha + sia nella colonna Y sia in quella Z.

 

Nella casella B, il numero 2 indica che in 2 coppie (I,II; III,IV) la variabile Y è discordante da X, mentre la variabile Z è concordante con X; in altri termini, mentre si ha il segno + nella colonna X si ha contemporaneamente il segno - nella colonna Y e quello + nella colonna Z.

 

Nella casella C, il numero 0 indica che non si ha alcuna coppia in cui variabile Y è concordante con X, mentre la variabile Z è discordante da X; in altri termini, non è presente alcun caso in cui si ha + nella colonna X, mentre si ha anche + nella colonna Y e contemporaneamente il segno - nella colonna Z.

 

Nella casella D, il numero 2 indica che in 2 coppie (I,II; II,III) la variabile Y e la variabile Z discordano simultaneamente dalla variabile X; in altri termini, nella casella D è riportato il numero di casi in cui si ha il segno - contemporaneamente sia nella variabile Y sia nella variabile Z, mentre ovviamente si ha il segno + nella variabile X.

 

Le caselle n₁, n₂, n₃, n₄ riportano i totali parziali.

Nella casella n₁ è riportato il numero di concordanze (8) tra la variabile X (+) e la variabile Z (+), senza considerare la variabile Y.

Nella casella n₂ è riportato il numero di discordanze (2) tra la variabile X (+) e la variabile Z (-), ignorando la variabile Y.

Nella casella n₃ è riportato il numero di concordanze (6) tra la variabile X (+) e la variabile Y (+), senza considerare la variabile Z.

Nella casella n₄ è riportato il numero di discordanze (4) tra la variabile X (+) e la variabile Y (-), senza considerare la variabile Z.

 

Una volta individuate concordanze e discordanze tra le tre variabili, il coefficiente di correlazione parziale  di Kendall, (la correlazione tra Y e Z tenendo costante X), è calcolata rapidamente mediante la relazione

 

 

Con i dati dell'esempio,

 

 

 si ottiene un valore di correlazione netta uguale a +0,61.

 

Trattandosi di un campione piccolo, per la sua significatività si utilizza la tabella precedente.

 

Nel caso di grandi campioni, data la complessità delle operazioni descritte, il metodo diventa di difficile applicazione, quando non si dispone di programmi informatici.

La significatività è fornita dal test Z; se è riportato solo il suo valore e non il numero di dati o dei gdl, la probabilità relativa è data dalla distribuzione normale.